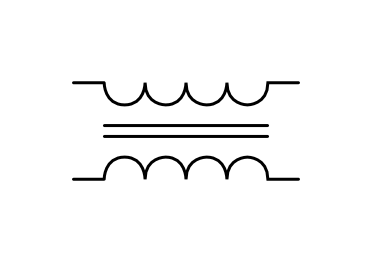
Transformatoren¶
Transformatoren sind Bauteile, die eine Wechselspannung (oder pulsierende Gleichspannung) in eine betragsmäßig höhere oder niedrigere Spannung umwandeln können.
Aufbau und Funktionsweise¶
Ein Transformator ist stets aus zwei Spulen aufgebaut, die sich auf den gegenüber liegenden Seiten eines Eisen- oder Ringkerns befinden. Die Spule, an der die Eingangsspannung anliegt, wird als Primärspule, die andere als Sekundärspule bezeichnet.
Das Verhältnis aus der Anzahl an Windungen 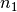 der Primärspule
zur Anzahl an Windungen
der Primärspule
zur Anzahl an Windungen 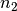 der Sekundärspule bestimmt das
Verhältnis von der Eingangsspannung
der Sekundärspule bestimmt das
Verhältnis von der Eingangsspannung 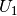 zur Ausgangsspannung
zur Ausgangsspannung
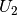 :
:
(1)¶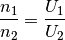
Die Stromstärken verhalten sich dabei genau umgekehrt wie die Spannungen:
(2)¶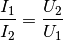
Damit wird von einem (idealen) Transformator genauso viel elektrische Leistung
aufgenommen wie abgegeben: 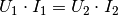 . In der Praxis
rechnet man zur Zahl der Windungen
. In der Praxis
rechnet man zur Zahl der Windungen 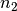 der Sekundärseite meist
der Sekundärseite meist
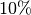 hinzu, um die Energieverluste durch das Aufwärmen des
Transformators auszugleichen.
hinzu, um die Energieverluste durch das Aufwärmen des
Transformators auszugleichen.
Beispiel:
Um die Netzspannung von
![U_1 = \unit[230]{V}](../_images/math/76b9972207fe06d4e6f1234cc1dd0fe0ae40e2be.png) auf beispielsweise
auf beispielsweise
![U_2 = \unit[12]{V}](../_images/math/24b70bd969917f7bae6fc3d55e900f418b2df3ee.png) herunter zu regeln, benötigt man folgendes
Verhältnis an Windungszahlen:
herunter zu regeln, benötigt man folgendes
Verhältnis an Windungszahlen:![\frac{n_1}{n_2} &= \frac{U_1}{U_2} = \frac{\unit[230]{V}}{\unit[12]{V}}
\approx 19,2 \\[10pt]
\Rightarrow n_1 &= 19,2 \cdot n_2](../_images/math/b51670e760880e96e1a981341d6bcdd0970c6d35.png)
Auf der Primärseite müssen also rund
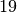 mal mehr Windungen
aufgebracht werden als auf der Sekundärseite.
mal mehr Windungen
aufgebracht werden als auf der Sekundärseite.
Werden die Eingangs- und Ausgangsanschlüsse des Transformators umgetauscht,
so kann man (theoretisch) mit dem gleichen Transformator eine Wechselspannung
von ![U_1 = \unit[12]{V}](../_images/math/4631c62ea1376fbb4f4594e73615f8c843482b44.png) auf
auf ![U_2 = \unit[230]{V}](../_images/math/1005b8325579fd96c91b2d525519bae9f6770db8.png) hochtransformieren.
hochtransformieren.
Exkurs: Schwach- und Starkstrom¶
Für die bei einem Verbraucher umgesetzte elektrische Leistung gilt 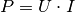 ; eine bestimmte
elektrische Leistung ist somit sowohl als Produkt eines hohen Spannungswerts mit
einer geringen Stromstärke oder umgekehrt als Produkt einer hohen Stromstärke
bei geringer Spannung denkbar. Im ersteren Fall müsste dann der elektrische
Widerstand des Verbrauchers hoch, im zweiten gering sein, wie folgendes Beispiel
zeigt:
; eine bestimmte
elektrische Leistung ist somit sowohl als Produkt eines hohen Spannungswerts mit
einer geringen Stromstärke oder umgekehrt als Produkt einer hohen Stromstärke
bei geringer Spannung denkbar. Im ersteren Fall müsste dann der elektrische
Widerstand des Verbrauchers hoch, im zweiten gering sein, wie folgendes Beispiel
zeigt:
Beispiel:
Ein Verbraucher mit einer einer elektrischen Leistung von
![P=\unit[100]{W}](../_images/math/6eddf6a5710d82b751c496396921d62dd1e0506a.png) soll so gebaut werden, dass er diese Leistung bei
einer Spannung von
soll so gebaut werden, dass er diese Leistung bei
einer Spannung von ![U_1 = \unit[12]{V}](../_images/math/4631c62ea1376fbb4f4594e73615f8c843482b44.png) beziehungsweise
beziehungsweise ![U_2 =
\unit[230]{V}](../_images/math/10b491f0e58568c8f7f677f459b1d0124b8d9a2c.png) liefern soll. Welche Widerstandswerte
liefern soll. Welche Widerstandswerte 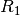 beziehungsweise
beziehungsweise 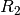 muss der Verbraucher in diesen beiden Fällen
aufweisen?
muss der Verbraucher in diesen beiden Fällen
aufweisen?Im ersten Fall muss zum Erreichen der Leistung
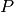 folgende Stromstärke
auftreten:
folgende Stromstärke
auftreten:![P = U_1 \cdot I_1 \quad \Longleftrightarrow \quad I_1 = \frac{P}{U_1} =
\frac{\unit[100]{W}}{\unit[12]{V}} \approx \unit[8,33]{A}](../_images/math/659ac08160baa92cd4eb154d4e39d2312c0e1f68.png)
Nach dem Ohmschen Gesetz ergibt sich damit folgender Widerstand:
![R_1 = \frac{U_1}{I_1} = \frac{\unit[12]{V}}{\unit[8,33]{A}} =
\unit[1,44]{\Omega}](../_images/math/de5601119c04c1ae6a3c0ec159a101c0529e8349.png)
Im zweiten Fall gilt für die Stromstärke
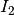 :
:![P = U_2 \cdot I_2 \quad \Longleftrightarrow \quad I_2 = \frac{P}{U_2} =
\frac{\unit[100]{W}}{\unit[230]{V}} \approx \unit[0,434]{A}](../_images/math/953944628c4ec44addc387d7b960216767d16f08.png)
Damit ergibt sich für den Widerstand
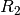 :
:![R_2 = \frac{U_2}{I_2} = \frac{\unit[230]{V}}{\unit[0,434]{A}} =
\unit[529]{\Omega}](../_images/math/2ca95e42f67b353042d0b172cf809a1066bad415.png)
Zunächst erscheinen beide Varianten als gleichwertig. Ein deutlicher Unterschied ergibt sich allerdings, wenn man den (geringen) elektrischen Widerstand der Leitungen mit berücksichtigt. Diese stellen zusammen mit dem eigentlichen Verbraucher eine Reihenschaltung von Widerständen dar; die Widerstandswerte der Leitung und des Verbrauchers müssen somit addiert werden.
Beispiel:
Die zwei Verbraucher aus dem obigen Beispiel (Widerstandswerte von
![R_1=\unit[1,44]{\Omega}](../_images/math/a735b3d91e69e77e5b373d84cc831fb5bdf4f4fd.png) beziehungsweise
beziehungsweise ![R_2 =
\unit[529]{\Omega}](../_images/math/3e9a83adaa0fc3fb5e8403928c6ecc1b2460a2b5.png) ) sollen mit den Spannungen
) sollen mit den Spannungen ![U_1 = \unit[12]{V}](../_images/math/4631c62ea1376fbb4f4594e73615f8c843482b44.png) beziehungsweise
beziehungsweise ![U_2 = \unit[230]{V}](../_images/math/1005b8325579fd96c91b2d525519bae9f6770db8.png) betrieben werden, wobei der
Widerstand der Leitungen auf
betrieben werden, wobei der
Widerstand der Leitungen auf ![R_0 = \unit[1]{\Omega}](../_images/math/b1df1b9e7f31aa59a030be66298f2844727f3e44.png) geschätzt werden
soll. Welche Leistungen
geschätzt werden
soll. Welche Leistungen 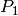 beziehungsweise
beziehungsweise 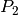 ergeben sich
dabei für die beiden Verbraucher?
ergeben sich
dabei für die beiden Verbraucher?Im ersten Fall ergibt sich ein Gesamtwiderstand von
![R_{1,\mathrm{ges}}
= R_0 + R_1 \approx \unit[(1,0 + 1,44)]{\Omega} = \unit[2,44]{\Omega}](../_images/math/02f4d1b4ad9551f0da579c33f445342e0ac597b1.png) . Somit
stellt sich folgende Stromstärke ein:
. Somit
stellt sich folgende Stromstärke ein:![I_1 = \frac{U_1}{R_{\mathrm{1,ges}}} \approx
\frac{\unit[12]{V}}{\unit[2,44]{\Omega}} \approx \unit[4,92]{A}](../_images/math/d5fef8d0d61bf14c448e9e4a0743fa36b7555e13.png)
Insgesamt beträgt die im Stromkreis umgesetzte elektrische Leistung in diesem Fall
![P_{\mathrm{1,ges}} = U_1 \cdot I_1 = \unit[12]{V} \cdot
\unit[4,92]{A} \approx \unit[59,0]{W}](../_images/math/2a8a0cf49a171feca38628137d822fac548cafe2.png) . Da es sich allerdings um eine
Reihenschaltung handelt, teilt sich die Spannung auf die beiden
Teilwiderstände (Leitung und Verbraucher) auf:
. Da es sich allerdings um eine
Reihenschaltung handelt, teilt sich die Spannung auf die beiden
Teilwiderstände (Leitung und Verbraucher) auf:![U_{\mathrm{1,Verbraucher}} &= R_1 \cdot I_1 \approx \unit[1,44]{\Omega}
\cdot \unit[4,92]{A} = \unit[7,08]{V}\\[4pt]
U_{\mathrm{1,Leitung}} &= R_0 \cdot I_1 = \unit[\phantom{,44}1]{\Omega} \cdot
\unit[4,92]{A} = \unit[4,92]{V}](../_images/math/6ccf88e2db9e1c00033af99251a6f25c5eb7542d.png)
Somit ergibt sich am Verbraucher eine elektrische Leistung von
![P_{\mathrm{1,Verbraucher}} = U_{\mathrm{1,Verbraucher}} \cdot I_1
\approx \unit[34,8]{W}](../_images/math/9b394e8fdc907d68ac65ecc0f647787bcbed0378.png) , während eine Leistung von
, während eine Leistung von
![P_{\mathrm{1,Leitung}} = U_{\mathrm{1,Leitung}} \cdot I_1 \approx
\unit[24,2]{W}](../_images/math/8fd591f386eb24fc353de8df0fe506edbb17dbc9.png) in Form von Wärme an die Leitung abgegeben wird.
in Form von Wärme an die Leitung abgegeben wird.Im zweiten Fall ergibt sich ein Gesamtwiderstand von
![R_{2,\mathrm{ges}}
= R_0 + R_2 = \unit[(1 + 529)]{\Omega} = \unit[530]{\Omega}](../_images/math/e7d37b0dfd7a4f920239a9e84de1a45cb7c2a850.png) . Somit stellt
sich folgende Stromstärke ein:
. Somit stellt
sich folgende Stromstärke ein:![I_2 = \frac{U_2}{R_{\mathrm{2,ges}}} =
\frac{\unit[230]{V}}{\unit[530]{\Omega}} \approx \unit[0,433]{A}](../_images/math/6b78483630807d3be52360bf7fef59309dc9e95c.png)
Insgesamt beträgt die im Stromkreis umgesetzte elektrische Leistung in diesem Fall
![P_{\mathrm{2,ges}} = U_2 \cdot I_2 = \unit[230]{V} \cdot
\unit[0,433]{A} \approx \unit[99,81]{W}](../_images/math/471429312a6307c8e2362ec4043a018feddf1e65.png) . Da es sich allerdings um eine
Reihenschaltung handelt, teilt sich die Spannung auf die beiden
Teilwiderstände (Leitung und Verbraucher) auf:
. Da es sich allerdings um eine
Reihenschaltung handelt, teilt sich die Spannung auf die beiden
Teilwiderstände (Leitung und Verbraucher) auf:![U_{\mathrm{2,Verbraucher}} &= R_2 \cdot I_2 \approx \unit[529]{\Omega}
\cdot \unit[0,433]{A} \approx \unit[229,57]{V} \\[4pt]
U_{\mathrm{2,Leitung}} &= R_0 \cdot I_2 = \unit[\phantom{52}1]{\Omega} \cdot
\unit[0,433]{A} = \unit[0,43]{V}](../_images/math/ac7f14c0ba047e75523566b752728d23b878b1c3.png)
Somit ergibt sich am Verbraucher eine elektrische Leistung von
![P_{\mathrm{2,Verbraucher}} = U_{\mathrm{2,Verbraucher}} \cdot I_2
\approx \unit[99,62]{W}](../_images/math/ac1538bafeb27d129e2742d2b68c97e6c4886f01.png) , während eine Leistung von
, während eine Leistung von
![P_{\mathrm{2,Leitung}} \approx \unit[0,18]{W}](../_images/math/45f6ee377b21648a6211274eb2cfc1eefc71ac48.png) in Form von Wärme an die
Leitung abgegeben wird.
in Form von Wärme an die
Leitung abgegeben wird.
Wie das obige Beispiel zeigt, wird Elektrizität unter Berücksichtigung des (geringen) elektrischen Widerstands realer Leitungen wesentlich effektiver bei hohen Spannungen transportiert, da hierbei Wärmeverluste minimiert werden; zudem spielt bei Verwendung hoher Spannungen der tatsächliche Wert der Leitungs-Widerstände, der je nach Länge der Anschluss-Kabel und Qualität der leitenden Verbindungen etwas variieren kann, kaum eine Rolle.
Mittels Transformatoren können die an den Leitungen anliegenden, verhältnismäßig hohen Spannungen können innerhalb der jeweiligen elektronischen Geräte dann wieder auf den gewünschten Wert angepasst werden.
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.