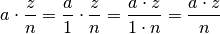Bruchrechnung¶
Für das Rechnen mit Bruchtermen gelten prinzipiell die gleichen Regeln wie für das Rechnen mit Bruchzahlen. Als Besonderheit ist allerdings stets darauf zu achten, dass der Nenner des Bruchs nicht den Wert Null annehmen darf, da eine Division durch Null nicht definiert ist. Diese Bedingung lässt sich gegebenenfalls durch eine Beschränkung des Definitionsbereichs der im Nenner auftretenden Variablen erreichen.
Erweitern und Vereinfachen¶
Ein Bruchterm 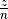 lässt sich jederzeit erweitern, indem sowohl
der Zähler
lässt sich jederzeit erweitern, indem sowohl
der Zähler  wie auch der Nenner
wie auch der Nenner 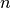 mit dem gleichen Faktor
mit dem gleichen Faktor
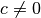 multipliziert werden. Es gilt somit:
multipliziert werden. Es gilt somit:
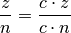
Ein Bruchterm lässt sich ebenso in umgekehrter Weise vereinfachen („kürzen“),
wenn sowohl der Zählerterm wie auch der Nennerterm einen gleichen Faktor
 (oder mehrere gleiche Faktoren
(oder mehrere gleiche Faktoren 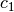 ,
, 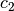 usw.)
beinhalten.
usw.)
beinhalten.
Beispiele:
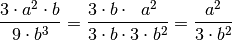
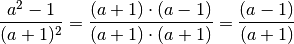
Besteht der Zähler und/oder der Nenner eines Bruchterms aus einer Summe von Termen, so ist ein Kürzen nicht unmittelbar möglich; vielmehr müssen der Zähler wie auch der Nenner jeweils vollständig in einzelne Faktoren zerlegt werden. Hierbei können insbesondere das Distributivgesetzes sowie binomische Formeln hilfreich sein:
Nach dem Distributivgesetz kann ein in allen Summanden des Zählers und/oder des Nenners auftretender Faktor ausgeklammert werden. Eine Summe kann damit als Produkt zweier Faktoren geschrieben werden.
Jede Summe
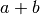 kann, sofern man sie in Klammern setzt, ebenfalls als
einzelner Faktor
kann, sofern man sie in Klammern setzt, ebenfalls als
einzelner Faktor 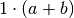 angesehen werden.[1] Somit gilt
beispielsweise:
angesehen werden.[1] Somit gilt
beispielsweise: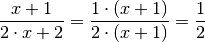
Entspricht der Zähler und/oder Nenner eines Bruches (oder zumindest einer der auftretenden Faktoren) dem Ergebnis einer binomischen Formel, so kann diese angewendet werden, um eine weitere Faktorisierung zu erreichen.
Ein Bruchterm, der zum Schluss einer Rechnung ein Endergebnis darstellt, wird üblicherweise in einer so weit wie möglich gekürzten Form angegeben.
Rechenregeln für Bruchterme¶
Da bei der Rechnung mit Bruchtermen üblicherweise mit reellen Zahlen oder entsprechenden Variablen gerechnet wird, gelten die drei Rechengesetze für Grundrechenarten in gleicher Form auch für Bruchterme. Als Besonderheit muss dabei stets darauf geachtet werden, dass der Nennerterm nicht den Wert Null annehmen darf.
Für 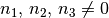 gilt:
gilt:
Kommutativgesetz:
![\frac{z_1}{n_1} + \frac{z_2}{n_2} &=
\frac{z_2}{n_2} + \frac{z_1}{n_1} {\color{white} \qquad \! \ldots}
\\[2pt]
\frac{z_1}{n_1} \, \cdot \; \frac{z_2}{n_2} &=
\frac{z_2}{n_2} \; \cdot \, \frac{z_1}{n_1}](../_images/math/8223d46cdb69d1186170204a61e8a4d1f3d99ce8.png)
Assoziativgesetz:
![\frac{z_1}{n_1} + \left( \frac{z_2}{n_2} + \frac{z_3}{n_3} \right)
&= \left( \frac{z_1}{n_1} + \frac{z_2}{n_2}\right) + \frac{z_3}{n_3}
{\color{white} \qquad \ldots} \\[2pt]
\frac{z_1}{n_1} \, \cdot \; \left( \frac{z_2}{n_2} \, \cdot \;
\frac{z_3}{n_3} \right) &= \left( \frac{z_ 1}{n_1} \, \cdot \;
\frac{z_2}{n_2}\right) \; \cdot \, \frac{z_3}{n_3}](../_images/math/3f5ef225c32f90effda7496ac36f3224520cbe25.png)
Distributivgesetz:
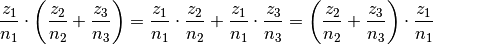
Auf weitere Besonderheiten, die sich bei der Verknüpfung von Bruchtermen durch die vier Grundrechenarten ergeben, wird in den folgenden Abschnitten näher eingegangen.
Addition und Subtraktion von Bruchtermen
Zwei Brüche lassen sich bei einer Addition oder Subtraktion nur dann direkt zusammenfassen, wenn sie „gleichnamig“ sind, d.h. den gleichen Nenner besitzen. Dabei werden die Zählerterme addiert, der Nennerterm bleibt unverändert:
(1)¶![\frac{z_1}{n} + \frac{z_2}{n} = \frac{z_1 + z_2}{n} \\[2pt]
\frac{z_1}{n} - \frac{z_2}{n} = \frac{z_1 - z_2}{n}](../_images/math/626a63e7ad8fd91a6538621ce472a95128c40f59.png)
Haben Brüche unterschiedliche Nennerterme, so müssen alle Brüche zunächst auf
einen gemeinsamen Nenner gebracht werden, bevor eine Addition beziehungsweise
Subtraktion möglich ist. Hierzu empfiehlt es sich, zunächst die Nennerterme
vollständig in einzelne Faktoren zu zerlegen. Von jedem Faktor, der in
mindestens einem der Nenner vorkommt, wählt man anschließend die jeweils höchste
Potenz aus und multipliziert diese Faktoren miteinander. Auf diese Weise erhält
man das kleinste gemeinsame Vielfache der Nennerterme 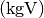 ,
das auch als „Hauptnenner“ bezeichnet wird.
,
das auch als „Hauptnenner“ bezeichnet wird.
Beispiele:
Entsprechen die Nenner dreier Brüche den Zahlen
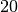 ,
, 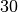 und
und
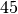 so lautet der Hauptnenner:
so lautet der Hauptnenner: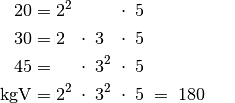
Bei einem Ausmultiplizieren der einzelnen Zahlen ohne Faktorisierung und Bildung des kleinsten gemeinsamen Vielfachen würde sich ein gemeinsamer Nenner von
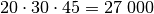 ergeben.
ergeben.Entsprechen die Nenner den Termen
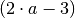 ,
, 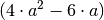 und
und 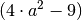 so lautet der Hauptnenner:
so lautet der Hauptnenner: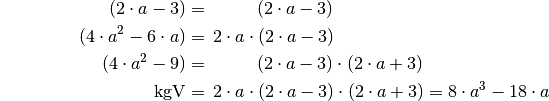
Bei einem Ausmultiplizieren der einzelnen Terme ohne Faktorisierung und Bildung des kleinsten gemeinsamen Vielfachen würde sich ein gemeinsamer Nenner von
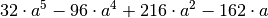 ergeben.
ergeben.
Die zu addierenden Brüche können anschließend um die fehlenden Faktoren erweitert und die Zählerterme nach obiger Gleichung addiert werden.
Multiplikation und Division von Bruchtermen
Bruchterme lassen sich miteinander multiplizieren, indem man sowohl ihre Zähler als auch ihre Nenner miteinander multipliziert:[2]
(2)¶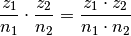
Um das Ergebnis in einer möglichst vereinfachten Form vorliegen zu haben, ist es (vor dem Ausmultiplizieren) sinnvoll, sowohl die Zähler wie auch die Nenner beider Brüche vollständig in Faktoren zu zerlegen. Kürzt man im Zähler und Nenner anschließend alle gemeinsamen Teiler, so erhält man als Endergebnis einen nicht weiter zu vereinfachenden Bruch.
Das Produkt aller gemeinsamen Teiler wird oftmals als „größter gemeinsamer
Teiler“ 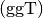 bezeichnet. Die explizite Berechnung des
bezeichnet. Die explizite Berechnung des
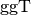 ist meist nicht erforderlich; die Aussage, dass sich durch
Kürzen des größten gemeinsamen Teilers von Zähler und Nenner ein nicht weiter zu
vereinfachender Bruch ergibt, gilt jedoch allgemein.
ist meist nicht erforderlich; die Aussage, dass sich durch
Kürzen des größten gemeinsamen Teilers von Zähler und Nenner ein nicht weiter zu
vereinfachender Bruch ergibt, gilt jedoch allgemein.
Bruchterme lassen sich durcheinander dividieren, indem man – durch Vertauschen von Zähler und Nenner – den Kehrbruch des Divisors bildet und eine Multiplikation nach obigem Schema durchführt:
(3)¶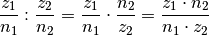
Auch hierbei ist eine Faktorisierung von Zähler und Nenner hilfreich, um das Endergebnis in einer möglichst vereinfachten Form zu erhalten. Das gleiche Verfahren kann genutzt werden, um so genannte Doppelbrüche aufzulösen:
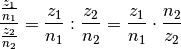
Bereits in der Antike fand Euklid
einen Algorithmus zur Berechnung des 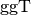 ; dieser ist auf der
Grund-Wissen-Seite im Rahmen des Python-Tutorials näher beschrieben.
; dieser ist auf der
Grund-Wissen-Seite im Rahmen des Python-Tutorials näher beschrieben.
Prozentrechnung¶
Bruchzahlen können auch verwendet werden, um Größenvergleiche anzugeben. Eine Bruchzahl beschreibt dabei das Verhältnis zweier Größen, d.h. welchen Bruchteil die eine Zahl (der Nenner) von der anderen Zahl (dem Zähler) ausmacht.
Um Zahlenverhältnisse vergleichen zu können, ist es oftmals hilfreich die
Bruchteile auf den selben Nenner zu bringen. Haben zwei Zahlen unterschiedliche
Zähler  und
und 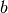 , aber einen gleichen Nenner
, aber einen gleichen Nenner 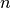 , so gilt
stets:
, so gilt
stets:

Als gemeinsamer Nenner wird in der Praxis meist die Zahl 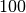 verwendet
und statt von Hundertsteln von Prozenten gesprochen. Für
verwendet
und statt von Hundertsteln von Prozenten gesprochen. Für 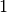 Prozent
schreibt man wahlweise
Prozent
schreibt man wahlweise 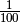 oder
oder 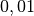 oder
oder 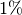 .
.
Die Anzahl der Prozente wird üblicherweise als Prozentsatz 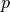 bezeichnet. Hierbei ist allerdings stets darauf zu achten, auf welchen Grundwert
bezeichnet. Hierbei ist allerdings stets darauf zu achten, auf welchen Grundwert
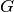 sich die Prozentangabe bezieht.
sich die Prozentangabe bezieht.
Beispiel:
Werden zu einem Grundwert von
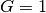 Liter Wasser ein Bruchteil von
Liter Wasser ein Bruchteil von
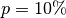 hinzu gegeben, so ergibt sich eine neue Menge
hinzu gegeben, so ergibt sich eine neue Menge 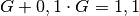 Liter.
Liter.Werden von dieser Menge (
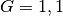 Liter) hingegen
Liter) hingegen 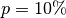 abgezogen, so bleiben nicht ein Liter, sondern „nur“
abgezogen, so bleiben nicht ein Liter, sondern „nur“ 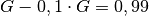 Liter übrig.
Liter übrig.
Der tatsächliche Wert, den eine Prozentangabe wiedergibt, wird Prozentwert
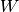 genannt. Er lässt sich als Produkt aus dem Prozentsatz
genannt. Er lässt sich als Produkt aus dem Prozentsatz 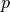 und
dem basierenden Grundwert
und
dem basierenden Grundwert 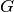 berechnen:
berechnen:
(4)¶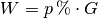
Im obigen Beispiel wurde die Prozentformel (4) bereits unmittelbar angewendet:
- Bezogen auf den Grundwert
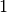 entspricht ein Prozentsatz von
entspricht ein Prozentsatz von 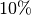 einem Prozentwert von
einem Prozentwert von 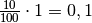 .
. - Bezogen auf den Grundwert
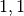 entspricht der gleiche Prozentsatz
einem Prozentwert von
entspricht der gleiche Prozentsatz
einem Prozentwert von 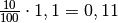 .
.
Wird der sich resultierende Prozentwert zum jeweiligen Grundwert addiert beziehungsweise von diesem abgezogen, so ergeben sich folglich auch unterschiedliche Ergebnisse.
Kleinere Mengenangaben werden häufig in Tausendstel (Promille) oder Millionstel
(Pars per Million) angegeben. Für 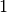 Promille schreibt man
Promille schreibt man
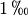 und für ein Millionstel
und für ein Millionstel ![\unit[1]{ppm}](../_images/math/6e7c2739431d9c03dda8122ca131aadc21090073.png) .
.
Anmerkungen:
| [1] | Hier wird wiederum das Distributivgesetz genutzt: Da für jede reelle
Zahl  die Beziehung die Beziehung 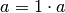 gilt, kann die gilt, kann die 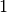 jederzeit als gemeinsamer Faktor einer beliebigen Summe ausgeklammert
werden.
jederzeit als gemeinsamer Faktor einer beliebigen Summe ausgeklammert
werden. |
| [2] |
Hierbei wird berücksichtigt, dass ein Zahlenwert unverändert bleibt, wenn man
ihn durch |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.