Vierecke¶
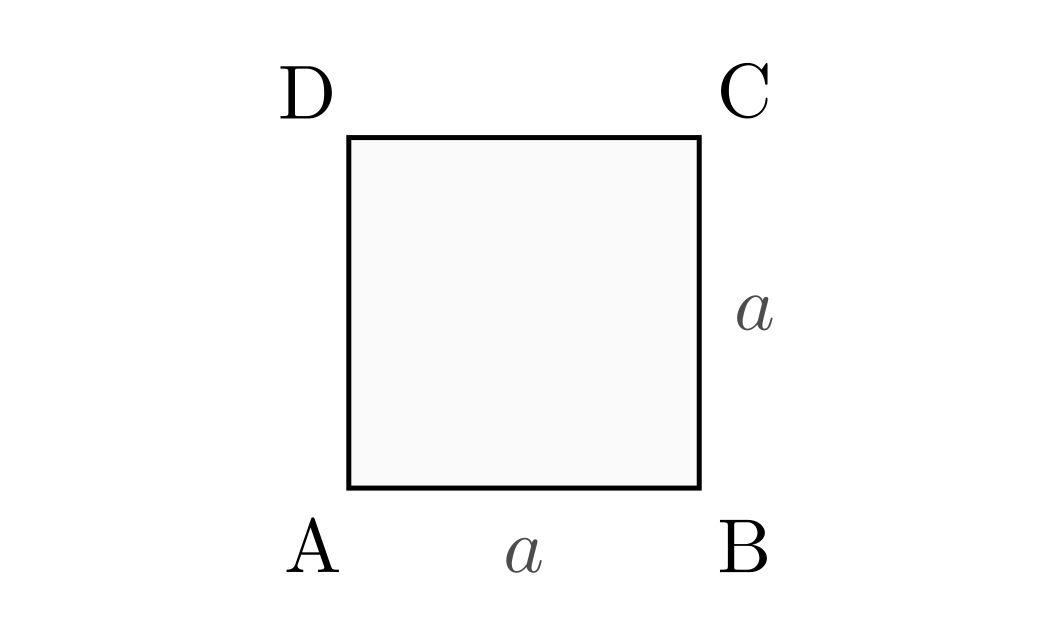
Das Quadrat
In einem Quadrat besitzen alle Seiten die gleiche Länge. Alle Winkel betragen
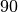 .
.
Quadrate haben folgende besondere Eigenschaft:
- Jedes Rechteck ist zweifach achsensymmetrisch; die beiden Symmetrieachsen verlaufen jeweils senkrecht durch die Mittelpunkte der Seiten.
- Die beiden Diagonalen sind gleich lang.
Für die Fläche und den Umfang eines Quadrats gilt:
![\text{Fl\"ache} &= a \cdot a = a^2 \\[10pt]
\text{Umfang} &= 4 \cdot a](../../_images/math/df130a68eb3488bf5466d94feee0f2837a42e646.png)
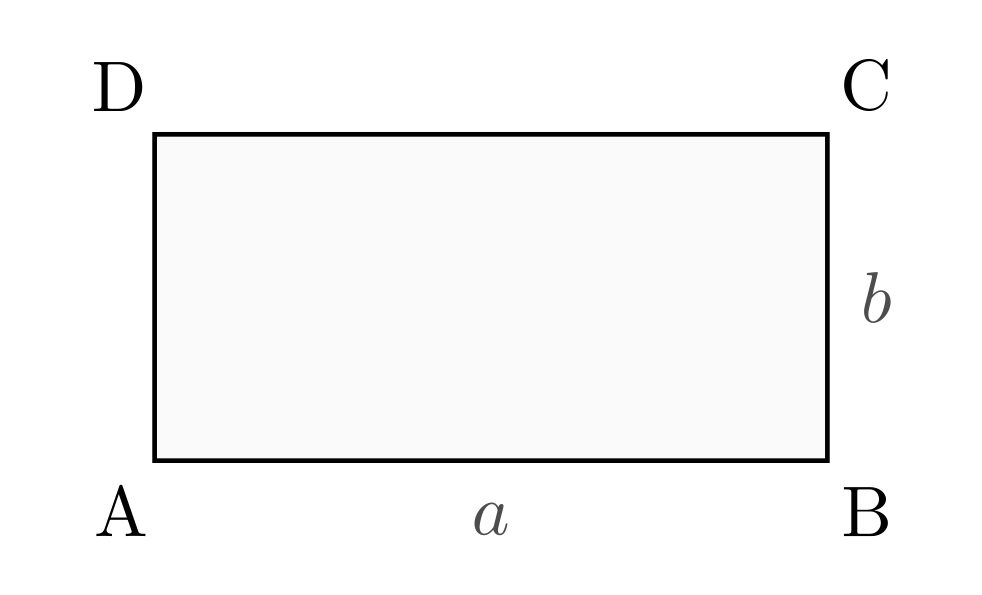
Das Rechteck
In einem Rechteck besitzen die jeweils gegenüber liegenden Seiten die gleiche
Länge. Alle Winkel betragen ![\unit[90]{\degree}](../../_images/math/ed42da9b82869c64cf4a98987530ceace4d59e0e.png) .
.
Rechtecke haben folgende besondere Eigenschaft:
- Jedes Rechteck ist zweifach achsensymmetrisch; die beiden Symmetrieachsen verlaufen jeweils senkrecht durch die Mittelpunkte der Seiten.
- Die beiden Diagonalen sind gleich lang.
Für die Fläche und den Umfang eines Rechtecks gilt:
![\text{Fl\"ache} &= a \cdot b \\[10pt]
\text{Umfang} &= 2 \cdot a + 2 \cdot b](../../_images/math/10552674079d7046ce30291899f537e8a5be6bd6.png)
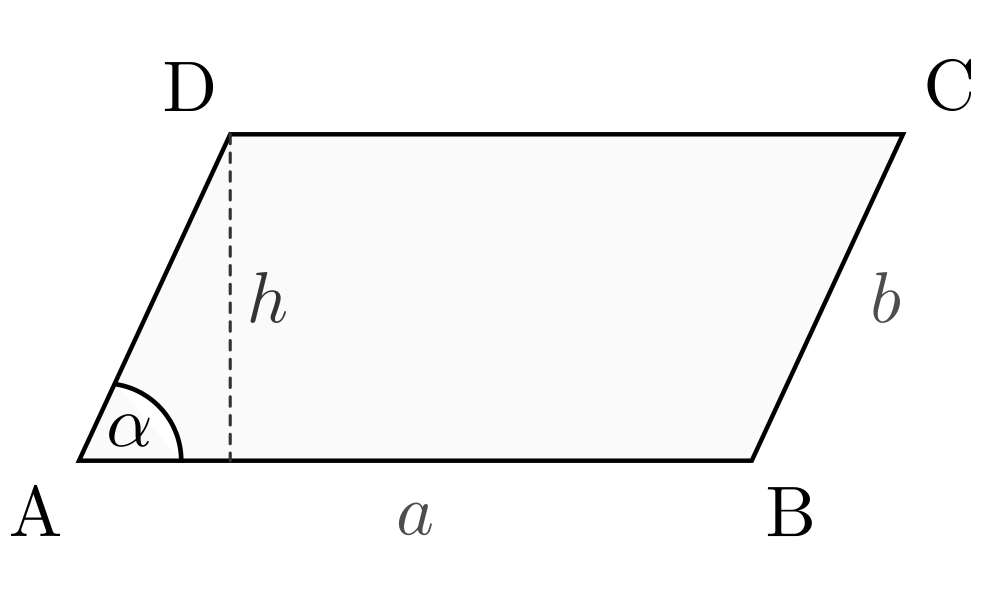
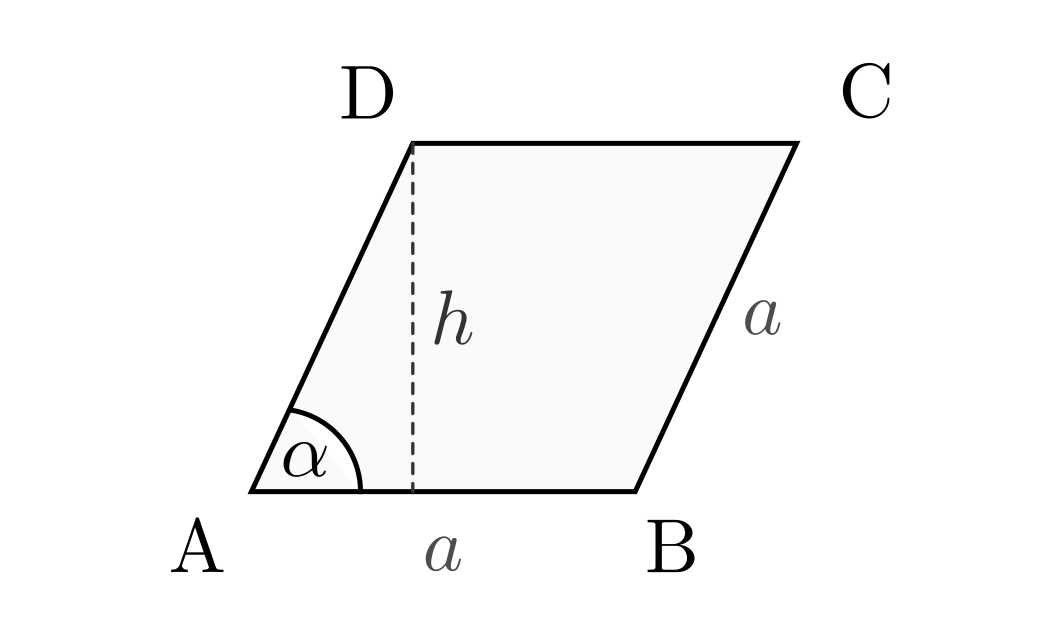
Das Parallelogramm
In einem Parallelogramm besitzen die jeweils gegenüber liegenden Seiten die gleiche Länge. Die jeweils gegenüber liegenden Winkel sind betragsmäßig gleich.
Parallelogramme haben folgende besondere Eigenschaft:
- Jedes Parallelogramm ist punktsymmetrisch bezüglich des Schnittpunkts der beiden Diagonalen.
- Die beiden Diagonalen halbieren sich gegenseitig.
- Je zwei benachbarte Winkel ergeben in Summe
![\unit[180]{\degree}](../../_images/math/a62139d45d177455d34d6e27e1030722257dea2f.png) .
.
Für die Fläche und den Umfang eines Parallelogramms gilt:
![\text{Fl\"ache} &= a \cdot b \cdot \sin{\alpha } = a \cdot h \\[10pt]
\text{Umfang} &= 2 \cdot a + 2 \cdot b](../../_images/math/655834d1a2df9fd90819a6a6d4de0e5a88b80d27.png)
Hat ein Parallelogramm vier gleich lange Seiten, so bezeichnet man es als „Rhombus“.
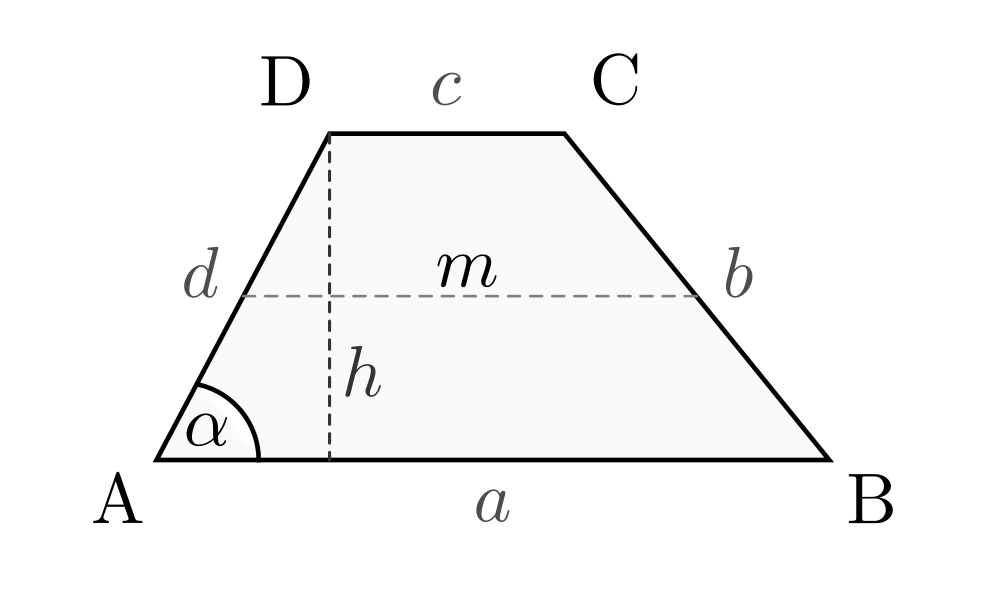
Das Trapez
Bei einem Trapez verlaufen (mindestens) zwei Seiten parallel zueinander.
Trapeze haben folgende besondere Eigenschaft:
Zeichnet man mittig zwischen die beiden parallel verlaufenden Seiten
 und
und  eine weitere parallele Strecke
eine weitere parallele Strecke 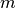 zwischen den übrigen
Seiten des Vierecks ein, so entspricht die Länge dieser als „Mittelparallele“
bezeichneten Strecke dem arithmetischen Mittelwert der beiden parallelen
Seiten:
zwischen den übrigen
Seiten des Vierecks ein, so entspricht die Länge dieser als „Mittelparallele“
bezeichneten Strecke dem arithmetischen Mittelwert der beiden parallelen
Seiten: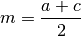
Für die Fläche und den Umfang eines Trapezes gilt:
![\text{Fl\"ache} &= \frac{a + c}{2} \cdot h = m \cdot h \\[10pt]
\text{Umfang} &= a + b + c + d](../../_images/math/46cd4ba494047c4dece3bdf81fb0f741c319f095.png)
Auch andere Sonderformen von Vierecken haben parallel verlaufende Seiten: Rhombus, Parallelogramm, Rechteck und Quadrat. Diese bereits beschriebenen Vierecke stellen somit Sonderformen eines Trapezes dar.
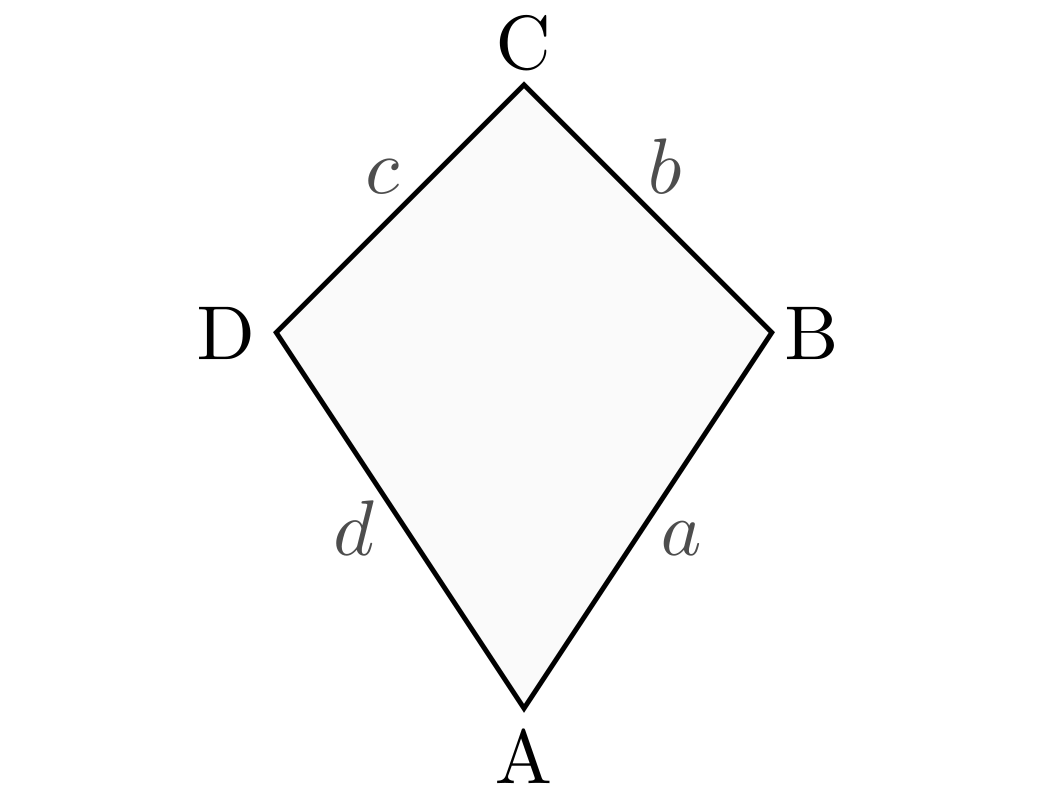
Das Drachenviereck
Bei einem Drachenviereck sind zwei aneinander anliegende Seiten  und
und
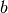 gleich lang; ebenso sind die beiden übrigen Seiten
gleich lang; ebenso sind die beiden übrigen Seiten  und
und 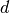 gleich lang.
gleich lang.
Drachenvierecke haben folgende besondere Eigenschaften:
- Jedes Drachenviereck hat senkrecht zueinander verlaufende Diagonalen.
- Jedes Drachenviereck kann in zwei gleichschenklige Dreiecke unterteilt werden
- Jedes Drachenviereck hat (mindestens) zwei gleich große Gegenwinkel.
- Jedes Drachenviereck ist achsensymmetrisch.
Die Kriterien eines Drachenvierecks werden auch von jedem Rhombus und jedem Quadrat erfüllt; diese Vierecke stellen somit Sonderformen eines Drachenvierecks dar.