Doppler-Effekt¶
Bewegen sich eine Schallquelle und/oder ein Schallempfänger aufeinander zu, so tritt der nach Christian Doppler benannte Doppler-Effekt auf. Aus dem Alltag kennt man zum Beispiel die Erfahrung, dass ein sich näherndes Fahrzeug Töne mit zunehmender Frequenz von sich gibt, während die Töne eines sich entfernenden Fahrzeugs zunehmend tiefer werden.
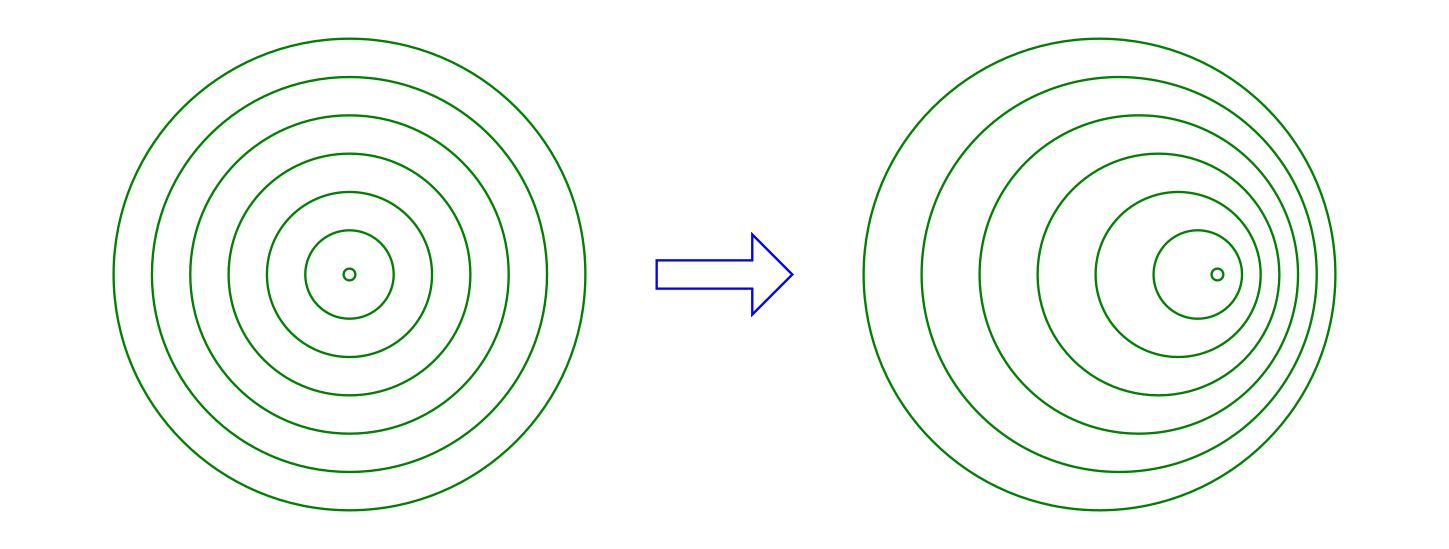
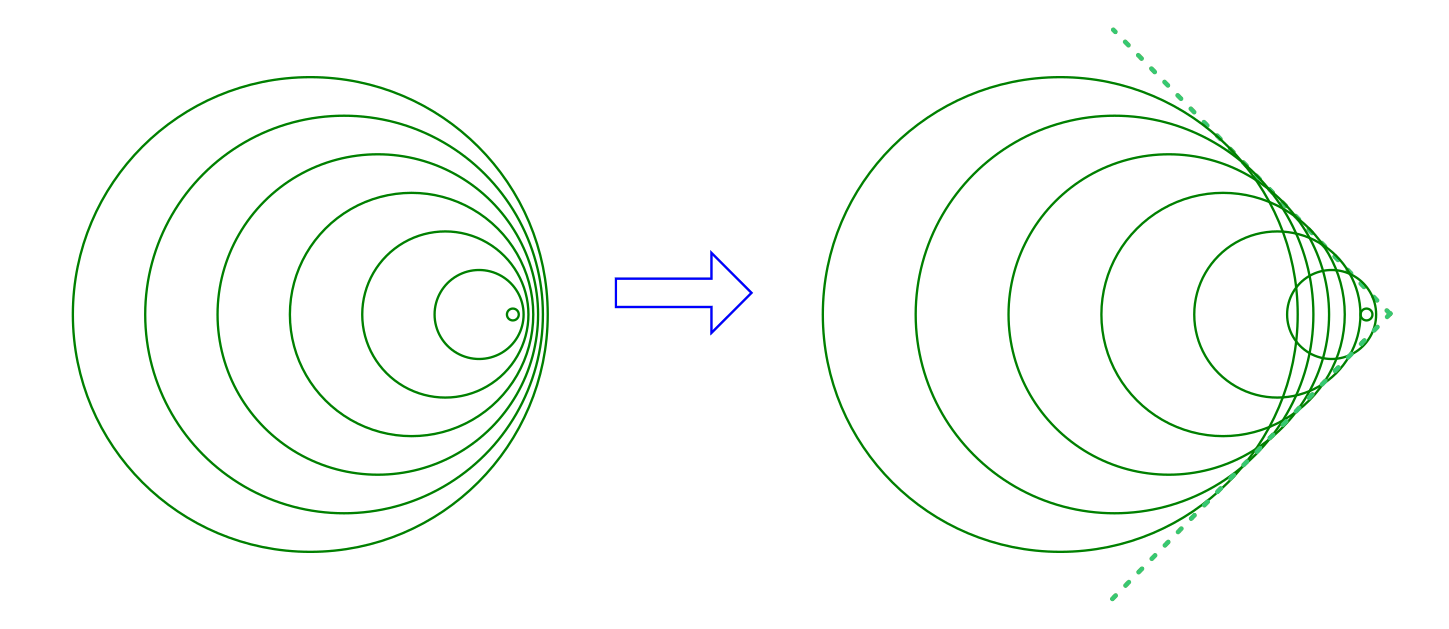
Wie man in der obigen Abbildung erkennen kann, werden die Abstände zwischen den
einzelnen ankommenden Schallwellen und somit die Wellenlängen 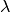 kürzer, wenn sich die Schallquelle auf den Beobachter zubewegt (der Beobachter
sich also am rechten Bildrand befindet). Umgekehrt erscheinen die Wellenlängen
als kürzer, wenn sich die Schallquelle vom Beobachter wegbewegt (der Beobachter
sich also am linken Bildrand befindet).
kürzer, wenn sich die Schallquelle auf den Beobachter zubewegt (der Beobachter
sich also am rechten Bildrand befindet). Umgekehrt erscheinen die Wellenlängen
als kürzer, wenn sich die Schallquelle vom Beobachter wegbewegt (der Beobachter
sich also am linken Bildrand befindet).
Bewegte Schallquelle, ruhender Beobachter
Da die Schallgeschwindigkeit 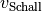 während des Vorgangs
konstant bleibt, muss sich gemäß der Wellenformel mit einer Änderung der
Wellenlänge
während des Vorgangs
konstant bleibt, muss sich gemäß der Wellenformel mit einer Änderung der
Wellenlänge 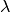 auch die Schallfrequenz
auch die Schallfrequenz 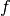 ändern:
ändern:
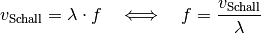
Nimmt der Beobachter bei einer sich nähernden Schallquelle eine verringerte
Wellenlänge 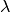 wahr, so muss sich folglich die wahrgenommene
Frequenz
wahr, so muss sich folglich die wahrgenommene
Frequenz 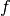 vergrößern. Quantitativ kann dieser Zusammenhang
folgendermaßen beschrieben werden:
vergrößern. Quantitativ kann dieser Zusammenhang
folgendermaßen beschrieben werden:

Möchte man den Einfluss auf die vom Beobachter empfangene Schallfrequenz
bestimmen, so muss auch 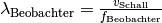 und
und 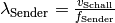 gesetzt
werden:
gesetzt
werden:
(1)¶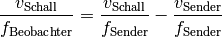
Diese Gleichung kann nach 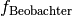 aufgelöst werden:
aufgelöst werden:
(2)¶![\frac{v_{\mathrm{Schall}}}{f_{\mathrm{Beobachter}}} &=
\frac{1}{f_{\mathrm{Sender}}} \cdot (v_{\mathrm{Schall}} -
v_{\mathrm{Sender}}) \\[8pt]
f_{\mathrm{Beobachter}} &= \frac{v_{\mathrm{Schall}}}{v_{\mathrm{Schall}} - v
_{\mathrm{Sender}}} \cdot f_{\mathrm{Sender}}](../_images/math/9405f72403300760143ec222f2804c79ff326196.png)
Das Minus-Zeichen in der obigen Gleichung gilt für eine sich nähernde Schallquelle; entfernt sich die Schallquelle vom Beobachter, so gilt die obige ebenfalls, wenn das Minus-Zeichen durch ein Plus-Zeichen ersetzt wird.
Beispiel:
Welche Frequenz wird von einem Beobachter wahrgenommen, wenn sich eine Schallquelle, die eine Frequenz von
![f_{\mathrm{Sender}}=\unit[440]{Hz}](../_images/math/2ac65e0b8d9e164d493c35512ec39c3005610725.png) aussendet, mit einer Geschwindigkeit von
aussendet, mit einer Geschwindigkeit von ![v_{\mathrm{Sender}} =
\unit[10]{\frac{m}{s}}](../_images/math/0cbb34578b99fdb0a82afb85db5e070233ed3255.png) auf den Beobachter zu- beziehungsweise wegbewegt?
auf den Beobachter zu- beziehungsweise wegbewegt?Im ersteren Fall gilt nach Gleichung (2) mit
![v_{\mathrm{Schall}} \approx \unit[340]{\frac{m}{s}}](../_images/math/585071ce2c681674cce73afa91e290d4e531443b.png) :
:![f_{\mathrm{Beobachter}} &= \frac{v_{\mathrm{Schall}}}{v_{\mathrm{Schall}}
- v_{\mathrm{Sender}}} \cdot f_{\mathrm{Sender}} =
\frac{\unit[340]{\frac{m}{s}}}{\unit[(340-10)]{\frac{m}{s}}} \cdot
\unit[440]{Hz} \approx \unit[453,3]{Hz}](../_images/math/ca87e31169685a5c31ec3c1034f14f5a3870d026.png)
Im zweiteren Fall muss das Minux-Zeichen der oberen Gleichung durch ein Plus-Zeichen ersetzt werden. Damit ergibt sich:
![f_{\mathrm{Beobachter}} &= \frac{v_{\mathrm{Schall}}}{v_{\mathrm{Schall}}
+ v_{\mathrm{Sender}}} \cdot f_{\mathrm{Sender}} =
\frac{\unit[340]{\frac{m}{s}}}{\unit[(340+10)]{\frac{m}{s}}} \cdot
\unit[440]{Hz} \approx \unit[427,4]{Hz}](../_images/math/4558cd629c1d7a1117a893b9e0ce4477fa0dad95.png)
Rotiert ein Lautsprecher wie beispielsweise im Leslie einer Hammond-Orgel kontinuierlich, so wird dadurch ebenfalls eine Frequenz-Schwingung um den eigentlich gespielten Ton hervorgerufen.
Bewegte Schallquelle und bewegter Beobachter
Bewegt sich nicht nur die Schallquelle mit einer Geschwindigkeit 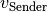 , sondern gleichzeitig auch der Beobachter mit der
Geschwindigkeit
, sondern gleichzeitig auch der Beobachter mit der
Geschwindigkeit 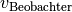 , so muss auch diese Bewegung
nach dem gleichen Prinzip in Gleichung (1)
berücksichtigt werden.
, so muss auch diese Bewegung
nach dem gleichen Prinzip in Gleichung (1)
berücksichtigt werden.
Bewegt sich der Beobachter auf die ihrerseits näher kommende Schallquelle zu, so gilt:
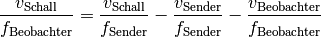
Diese Gleichung kann wiederum nach 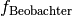 aufgelöst
werden:
aufgelöst
werden:
![\frac{v_{\mathrm{Schall}}}{f_{\mathrm{Beobachter}}} + \frac{v
_{\mathrm{Beobachter}}}{f_{\mathrm{Beobachter}}} &=
\frac{v_{\mathrm{Schall}}}{f_{\mathrm{Sender}}} - \frac{v
_{\mathrm{Sender}}}{f_{\mathrm{Sender}}} \\[8pt]
\frac{1}{f_{\mathrm{Beobachter}}} \cdot (v_{\mathrm{Schall}} + v
_{\mathrm{Beobachter}}) &= \frac{1}{f_{\mathrm{Sender}}} \cdot
(v_{\mathrm{Schall}} - v_{\mathrm{Sender}}) \\[8pt]](../_images/math/47b1d8aa9ec2806e531b62f91c28ae10c0e1266b.png)
Damit ergibt sich folgende allgemeinere Formel für den Doppler-Effekt:
(3)¶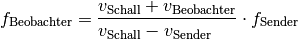
Die Vorzeichen in der obigen Formel gelten für sich aufeinander zu bewegende Schallquellen und Beobachter. Bewegt sich der Beobachter von der ursprünglichen Position der Schallquelle weg, so muss im Zähler ein Minus-Zeichen gesetzt werden; entfernt sich die Schallquelle vom ursprünglichen Ort des Beobachters, so muss im Zähler ein Plus-Zeichen gesetzt werden.
Schallmauer und Mach-Kegel
Mit einer zunehmenden Relativ-Geschwindigkeit der Schallquelle gegenüber dem
Beobachter wird auch der Doppler-Effekt immer ausgeprägter. Eine Besonderheit
ergibt sich, wenn sich die Geschwindigkeit der Schallquelle
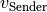 der Schallgeschwindigkeit
der Schallgeschwindigkeit
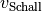 annähert.
annähert.
Erreicht die Schallquelle die Geschwindigkeit 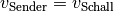 , so überlagern sich die von der Schallquelle ausgesendeten
Schallwellen konstruktiv mit jenen, die sie bereits vorher ausgesendet hatte.
Für die Schallquelle bedeutet dies einen erheblichen „Wellenberg“ (ein ein
Maximum an Luftdruck), der zum weiteren Beschleunigen überwunden werden muss;
Überschall-Flugzeuge müssen also beim „Durchbrechen der Schallmauer“ erhebliche
mechanische Belastungen aushalten; mit Überschallgeschwindigkeit nimmt der
Luftwiderstand zunächst wieder ab.[1]
, so überlagern sich die von der Schallquelle ausgesendeten
Schallwellen konstruktiv mit jenen, die sie bereits vorher ausgesendet hatte.
Für die Schallquelle bedeutet dies einen erheblichen „Wellenberg“ (ein ein
Maximum an Luftdruck), der zum weiteren Beschleunigen überwunden werden muss;
Überschall-Flugzeuge müssen also beim „Durchbrechen der Schallmauer“ erhebliche
mechanische Belastungen aushalten; mit Überschallgeschwindigkeit nimmt der
Luftwiderstand zunächst wieder ab.[1]
Für Beobachter auf dem Boden ist die Situation eine andere: Sie hören einen heftigen Knall, wenn sie vom nach Ernst Mach benannten „Mach-Kegel“ gestreift werden. Dieser Kegel entspricht der einhüllenden Kurve der (rechts in Abbildung Doppler-Effekt und Mach-Kegel gestrichelt dargestellt) kugelförmigen Schallwellen.[2] Der Knall ist also nicht nur in dem Moment beziehungsweise in der Nähe der Stelle hörbar, wenn das Flugzeug die Schallmauer durchbricht, sondern während der gesamten Dauer des Überschall-Fluges an jeder Stelle, die vom Mach-Kegel gestreift wird.
Anmerkungen:
| [1] | Wird eine Geschwindigkeit  als Vielfaches der
Schallgeschwindigkeit ausgedrückt, so bezeichnet man den sich ergebenden
Wert als „Mach-Zahl“. Eine Geschwindigkeit von als Vielfaches der
Schallgeschwindigkeit ausgedrückt, so bezeichnet man den sich ergebenden
Wert als „Mach-Zahl“. Eine Geschwindigkeit von ![v=\unit[1]{Mach}](../_images/math/e38e596ef4ddcec9e229f9b28b623a0fb1a26e71.png) ist
also mit der Schallgeschwindigkeit ist
also mit der Schallgeschwindigkeit ![v_{\mathrm{Schall}} \approx
\unit[340]{\frac{m}{s}}](../_images/math/220dda9aff35c18a63970bb601ebd927df3fc6e8.png) identisch. identisch. |
| [2] | Boote, die sich schnell über das Wasser bewegen, ziehen ebenfalls einen „flachen Kegel“ an Wellen hinter sich her. Einen Mach-Kegel kann man sich ähnlich vorstellen, nur eben dreidimensional. Je höher die Geschwindigkeit des Bootes beziehungsweise Überschallflugzeugs ist, desto „schmaler“ und „länger“ wird der Kegel. |

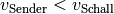 beziehungsweise
beziehungsweise
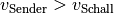 .
.