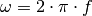Mathematische Beschreibung harmonischer Schwingungen¶
Die mathematische Beschreibung eines harmonisch schwingenden Gegenstands („Oszillators“) wird häufig als Basis-Modell in der theoretischen Physik genutzt. In diesem Abschnitt wird daher das grundlegende mathematische Konzept kurz vorgestellt.
Schwingungsgleichungen¶
Ein Körper führt genau dann eine harmonische Schwingung aus, wenn auf ihn eine Kraft wirkt, die proportional zu seiner Auslenkung ist und stets in Richtung der Ruhelage zeigt; die Dämpfung der Schwingung sollte vernachlässigbar gering ist.
Das Federpendel¶
In guter Näherung werden diese Bedingungen von einem Pendelkörper, der an einer
hängenden Schraubenfeder befestigt ist, erfüllt. Bei einer Auslenkung  aus der Ruhelage ist die rücktreibende Kraft gleich der Spannkraft
aus der Ruhelage ist die rücktreibende Kraft gleich der Spannkraft
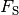 der Schraubenfeder. Diese hängt von der Federhärte
der Schraubenfeder. Diese hängt von der Federhärte
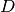 ab und ist der Auslenkung entgegengesetzt:
ab und ist der Auslenkung entgegengesetzt:

Die Kraft ruft im schwingenden Gegenstand eine Beschleunigung  hervor,
die nach dem Kraftgesetz als
hervor,
die nach dem Kraftgesetz als 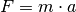 beschrieben werden kann,
wobei
beschrieben werden kann,
wobei 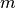 die Masse des Oszillators symbolisiert. Die Beschleunigung
die Masse des Oszillators symbolisiert. Die Beschleunigung
 entspricht nun gerade der zeitlichen Änderung der Geschwindigkeit,
welche wiederum einer zeitlichen Änderung des Ortes beziehungsweise der
Auslenkung entspricht.
entspricht nun gerade der zeitlichen Änderung der Geschwindigkeit,
welche wiederum einer zeitlichen Änderung des Ortes beziehungsweise der
Auslenkung entspricht.
Aus mathematischer Sicht sind die zur Auslenkung  proportionale Kraft
und ihre zur Beschleunigung
proportionale Kraft
und ihre zur Beschleunigung 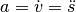 proportionale Wirkung
über eine zweifache zeitliche Ableitung miteinander gekoppelt. Es gilt somit:
proportionale Wirkung
über eine zweifache zeitliche Ableitung miteinander gekoppelt. Es gilt somit:
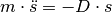
Diese Gleichung kann so umsortiert werden, dass beide von der Auslenkung
 abhängigen Größen auf der linken Seite stehen:
abhängigen Größen auf der linken Seite stehen:
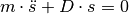
Noch deutlicher wird der Charakter dieser „Differentialgleichung“, wenn man die
Gleichung durch die Masse 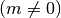 teilt:
teilt:
(1)¶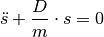
Diese Gleichung wird von jeder zeitabhängigen Funktion 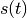 erfüllt,
deren zweite zeitliche Ableitung der ursprünglichen Funktion bis auf einen
konstanten Faktor identisch ist. Eine bekannte Funktion, die diese Bedingung
erfüllt, ist die Sinus-Funktion.
Ein Ansatz für den zeitlichen Verlauf der Auslenkung
erfüllt,
deren zweite zeitliche Ableitung der ursprünglichen Funktion bis auf einen
konstanten Faktor identisch ist. Eine bekannte Funktion, die diese Bedingung
erfüllt, ist die Sinus-Funktion.
Ein Ansatz für den zeitlichen Verlauf der Auslenkung  kann somit
folgendermaßen lauten:
kann somit
folgendermaßen lauten:
(2)¶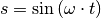
Dabei gibt  die so genannte „Oszillator-Frequenz“ an. Sie erinnert
an die Winkelgeschwindigkeit einer kreisförmigen
Bewegung, denn multipliziert mit der Zeit
die so genannte „Oszillator-Frequenz“ an. Sie erinnert
an die Winkelgeschwindigkeit einer kreisförmigen
Bewegung, denn multipliziert mit der Zeit 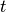 beschreibt sie den Ort, an
dem sich der periodisch schwingende Körper gerade befindet.[1]
beschreibt sie den Ort, an
dem sich der periodisch schwingende Körper gerade befindet.[1]
Bildet man für den Ansatz (2)  die
erste und zweite zeitliche Ableitung der Sinus-Funktion, so erhält man unter
Berücksichtigung der Kettenregel:
die
erste und zweite zeitliche Ableitung der Sinus-Funktion, so erhält man unter
Berücksichtigung der Kettenregel:
![\dot{s} &= \phantom{+} \omega \cdot \cos{(\omega \cdot t)} \\[10pt]
\ddot{s} &= - \omega ^2 \cdot \sin{(\omega \cdot t)}](../../_images/math/e0a8059dc5f7ed4a598da167956a68a78d0a48e0.png)
Die zweite zeitliche Ableitung 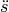 ist somit mit der ursprünglichen
Sinus-Funktion (2), welche die Auslenkung
ist somit mit der ursprünglichen
Sinus-Funktion (2), welche die Auslenkung
 beschreibt, bis auf einen Faktor
beschreibt, bis auf einen Faktor 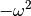 identisch:
identisch:
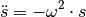
Dieses Ergebnis kann direkt in Gleichung (1) eingesetzt werden. Es folgt:
(3)¶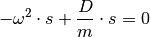
Auf der linken Seite kann  ausgeklammert werden. Es ergibt sich:
ausgeklammert werden. Es ergibt sich:
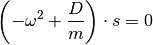
Diese Gleichung ist einerseits erfüllt, wenn 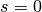 gilt, der Körper sich
also in der Ruhelage befindet. Andererseits gilt das Gleichheitszeichen für jede
beliebige Auslenkung, wenn der eingeklammerte Ausdruck als ganzes gleich Null
ist. Somit gilt:
gilt, der Körper sich
also in der Ruhelage befindet. Andererseits gilt das Gleichheitszeichen für jede
beliebige Auslenkung, wenn der eingeklammerte Ausdruck als ganzes gleich Null
ist. Somit gilt:
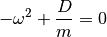
und damit:
(4)¶
Die Oszillator-Frequenz des schwingenden Pendelkörpers ist somit umso größer,
desto größer die Federkonstante („Härte“) 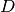 der Schraubenfeder ist.
Andererseits schwingt der Oszillator umso schneller, desto geringer seine Masse
der Schraubenfeder ist.
Andererseits schwingt der Oszillator umso schneller, desto geringer seine Masse
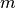 ist.
ist.
Die Weg-Zeit-Funktion 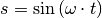 kann auch graphisch
als Diagramm dargestellt werden. Es ergibt sich der für harmonische
Schwingungen typische sinusförmige Verlauf. Je schneller der Pendelkörper
schwingt, desto schmäler werden die „Berge und Täler“ der Sinus-Kurve; je
größer die maximale Auslenkung ist, desto höher bzw. tiefer liegen die Hoch-
und Tiefpunkte.
kann auch graphisch
als Diagramm dargestellt werden. Es ergibt sich der für harmonische
Schwingungen typische sinusförmige Verlauf. Je schneller der Pendelkörper
schwingt, desto schmäler werden die „Berge und Täler“ der Sinus-Kurve; je
größer die maximale Auslenkung ist, desto höher bzw. tiefer liegen die Hoch-
und Tiefpunkte.
Die Sinus-Funktion eignet sich als Ansatz, wenn der Pendelkörper zu Beginn in der Ruhelage ist und in dieser Position von außen „angestoßen“ wird. Ist der maximal ausgelenkt und wird von dieser Position aus losgelassen, so ist die Kosinus-Funktion als Ansatz besser geeignet.
Die oben hergeleiteten Ergebnisse lassen sich beispielsweise auch auf die Schwingungen eines gefederten Fahrzeugs oder einer gefedert gelagerten Maschine (z.B. Waschmaschine) übertragen.
Das Fadenpendel¶
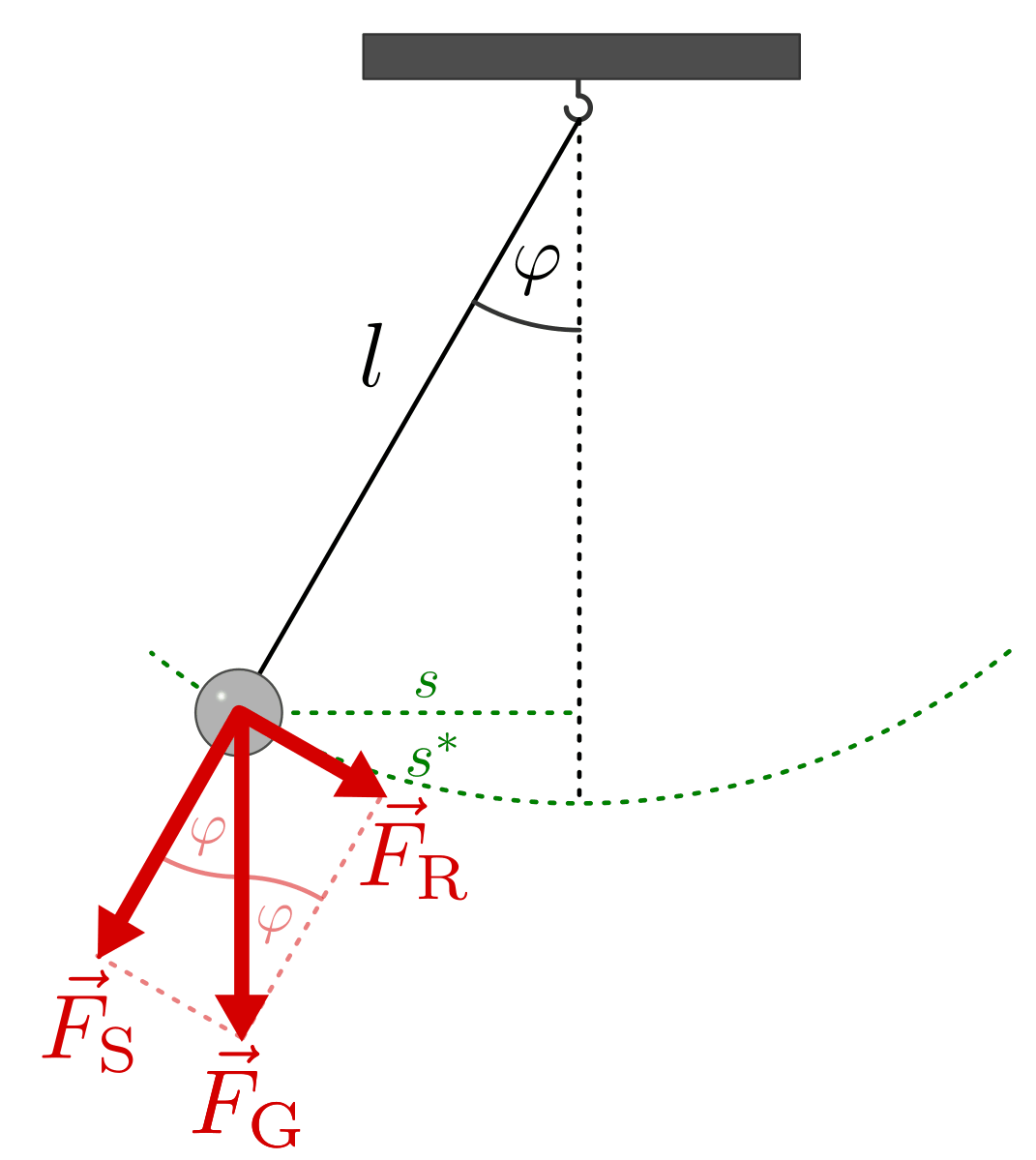
Auch Schwingungen eines Fadenpendels haben – bei nicht zu großer Auslenkung des Pendelkörpers – annähernd einen sinusförmigen Verlauf. Ist die Masse des Fadens vernachlässigbar klein und die Größe des Pendelkörpers klein im Vergleich zur Fadenlänge, so spricht man von einem mathematischen Pendel.
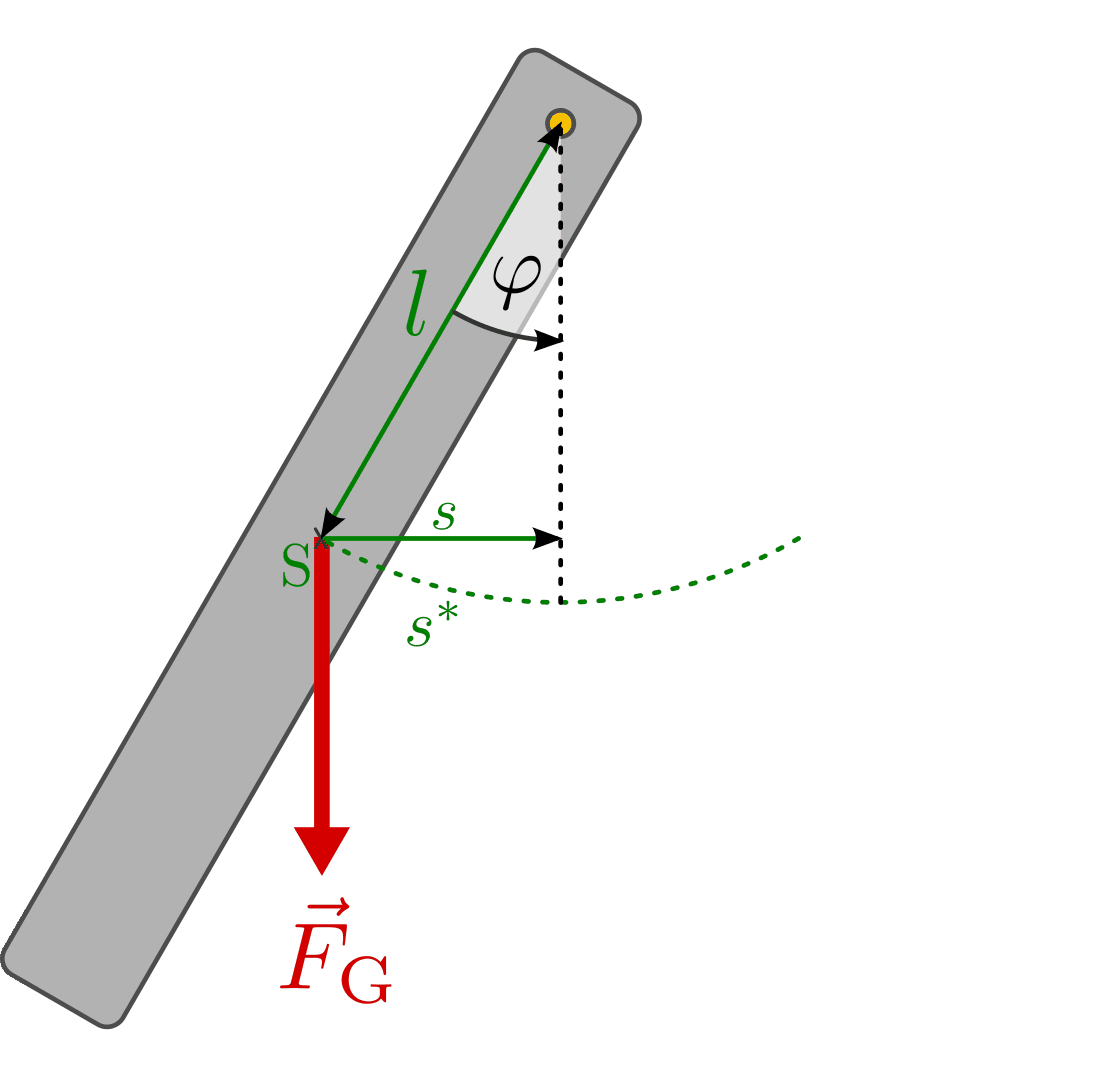
Die rücktreibend wirkende Kraft einer Pendelschwingung lässt sich bestimmen,
indem man die Gewichtskraft 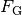 des Pendelkörpers in zwei
Teilkräfte (längs und quer zur
Schwingungsrichtung) zerlegt: Die Teilkraft
des Pendelkörpers in zwei
Teilkräfte (längs und quer zur
Schwingungsrichtung) zerlegt: Die Teilkraft 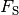 in
Seilrichtung hält den Faden gespannt, die Teilkraft
in
Seilrichtung hält den Faden gespannt, die Teilkraft 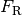 in
Schwingungsrichtung entspricht der rücktreibenden Kraft. Ist der
Auslenkungswinkel
in
Schwingungsrichtung entspricht der rücktreibenden Kraft. Ist der
Auslenkungswinkel 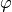 klein, so ist die Länge
klein, so ist die Länge 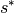 des
Kreisbogens näherungsweise gleich dem waagrechten Abstand
des
Kreisbogens näherungsweise gleich dem waagrechten Abstand  des
Pendelkörpers von der Ruhelage.[2]
des
Pendelkörpers von der Ruhelage.[2]
Für die rücktreibende Kraft 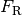 gilt mit
gilt mit
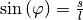 :
:
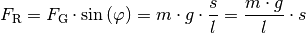
Der Term 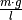 hat somit die gleiche Bedeutung für das
Fadenpendel wie die Federhärte
hat somit die gleiche Bedeutung für das
Fadenpendel wie die Federhärte 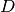 für das Federpendel. Man bezeichnet
ihn daher auch als „Richtgröße“
für das Federpendel. Man bezeichnet
ihn daher auch als „Richtgröße“ 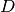 eines mathematischen Pendels. Man kann
also wiederum schreiben:
eines mathematischen Pendels. Man kann
also wiederum schreiben:
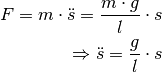
Für die Oszillatorfrequenz eines mathematischen Pendels gilt somit nach den Gleichungen (3) und (4):
(5)¶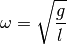
Experimentell bestätigt sich, dass die Schwingungsfrequenz eines Fadenpendels
zwar von der Länge 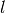 des Pendels, aber nicht von der Masse des
Pendelkörpers abhängig ist. Bei kleinen Auslenkungen
des Pendels, aber nicht von der Masse des
Pendelkörpers abhängig ist. Bei kleinen Auslenkungen 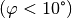 ist die Frequenz bzw. Schwingungsdauer zudem unabhängig von der
Amplitude.
ist die Frequenz bzw. Schwingungsdauer zudem unabhängig von der
Amplitude.
Pendel, bei denen die obigen Bedingungen erfüllt sind, nennt man Fadenpendel oder auch mathematische Pendel. Im Gegensatz dazu bezeichnet man beliebige, drehbar aufgehängte Gegenstände als physikalische Pendel.
Das physikalische Pendel¶
Führt ein beliebiges, drehbar gelagertes Objekt Schwingungsbewegungen aus, so können diese bei nur kleinen Auslenkungen und bei Vernachlässigung des Luftwiderstands ebenfalls als harmonische Schwingungen beschrieben werden.
Die rücktreibende Größe ist in diesem Fall das Drehmoment 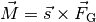 des Körperschwerpunkts bezüglich der Drehachse;
dabei bezeichnet
des Körperschwerpunkts bezüglich der Drehachse;
dabei bezeichnet  den horizontalen Abstand des Schwerpunkts von der
Ruhelage. Bei einem kleinen Auslenkungswinkel
den horizontalen Abstand des Schwerpunkts von der
Ruhelage. Bei einem kleinen Auslenkungswinkel 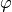 kann für den
Betrag des Drehmoments folgendes geschrieben werden:
kann für den
Betrag des Drehmoments folgendes geschrieben werden:
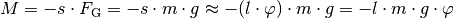
Hierbei wurde die Näherung 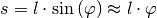 verwendet; das negative Vorzeichen berücksichtigt die Auslenkung in
negative
verwendet; das negative Vorzeichen berücksichtigt die Auslenkung in
negative 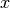 -Richtung. Für das Drehmoment
-Richtung. Für das Drehmoment 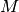 gilt allerdings
ebenso folgender Zusammenhang:
gilt allerdings
ebenso folgender Zusammenhang:
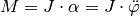
Hierbei steht 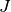 für das Trägheitsmoment des
schwingenden Gegenstands bezüglich dem Aufhängengepunkt und
für das Trägheitsmoment des
schwingenden Gegenstands bezüglich dem Aufhängengepunkt und 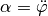 für die Winkelbeschleunigung. Setzt man beide Terme gleich, erhält man folgende
Differentialgleichung:
für die Winkelbeschleunigung. Setzt man beide Terme gleich, erhält man folgende
Differentialgleichung:
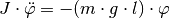
Wählt man als Lösung der Differentialgleichung wiederum 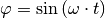 , so gilt wegen
, so gilt wegen 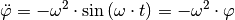 :
:
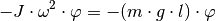
Für 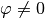 ergibt sich damit für die Oszillator-Frequenz
ergibt sich damit für die Oszillator-Frequenz
 eines physikalischen Pendels:
eines physikalischen Pendels:
(6)¶
Die Oszillator-Frequenz  eines physikalischen Pendels hängt somit
von der Masse des schwingenden Objekts, der Lage seines Schwerpunkts sowie von
seinem Trägheitsmoment bezüglich dem Aufhängepunkt ab. Bei dieser Frequenz sind
ebenfalls Resonanz-Effekte am
stärksten ausgeprägt.
eines physikalischen Pendels hängt somit
von der Masse des schwingenden Objekts, der Lage seines Schwerpunkts sowie von
seinem Trägheitsmoment bezüglich dem Aufhängepunkt ab. Bei dieser Frequenz sind
ebenfalls Resonanz-Effekte am
stärksten ausgeprägt.
In den obigen Gleichungen wurde mit 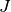 jeweils das Trägheitsmoment des
physikalischen Pendels um seinen Aufhängepunkt bezeichnet. Nach dem Satz
von Steiner gilt für dieses
jeweils das Trägheitsmoment des
physikalischen Pendels um seinen Aufhängepunkt bezeichnet. Nach dem Satz
von Steiner gilt für dieses 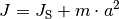 , wobei
, wobei 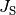 für das Trägheitsmoment des
Gegenstands bei einer Rotation um seinen Schwerpunkt und
für das Trägheitsmoment des
Gegenstands bei einer Rotation um seinen Schwerpunkt und  für den
Abstand des Schwerpunkts von der Drehachse steht. Mit
für den
Abstand des Schwerpunkts von der Drehachse steht. Mit 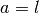 ergibt sich
damit folgende Gleichung für das Trägheitsmoment
ergibt sich
damit folgende Gleichung für das Trägheitsmoment 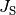 des
schwingenden Gegenstands:
des
schwingenden Gegenstands:
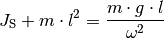
Diese Gleichung kann noch mit Hilfe der Beziehung 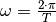 zwischen der Winkelgeschwindigkeit
zwischen der Winkelgeschwindigkeit  und der
Schwingungsdauer
und der
Schwingungsdauer 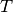 umformuliert werden. Es ergibt sich damit folgende
Gleichung:
umformuliert werden. Es ergibt sich damit folgende
Gleichung:
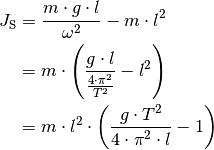
Diese Gleichung kann beispielsweise zur experimentellen Bestimmung des Trägheitsmoments eines Gegenstands genutzt werden kann, da alle darin vorkommenden Größen konstant oder leicht messbar sind.
Energiebilanz beim Feder- und Fadenpendel¶
Die Beziehung zwischen der Geschwindigkeit  des Pendelkörpers bei einer
harmonischen Schwingung und der Winkelgeschwindigkeit („Kreisfrequenz“)
des Pendelkörpers bei einer
harmonischen Schwingung und der Winkelgeschwindigkeit („Kreisfrequenz“)
 einer ebenso „schnellen“ Rotationsbewegung kann auch ohne
Differentialrechnung hergeleitet werden, wenn man die Energiebilanz der
Schwingung betrachtet. Nach dem Energie-Erhaltungssatz ist die maximale
kinetische Energie (beim Durchgang durch die Ruhelage) gleich der maximalen
potentiellen Energie (am Umkehrpunkt). Bei einem Federpendel ist
einer ebenso „schnellen“ Rotationsbewegung kann auch ohne
Differentialrechnung hergeleitet werden, wenn man die Energiebilanz der
Schwingung betrachtet. Nach dem Energie-Erhaltungssatz ist die maximale
kinetische Energie (beim Durchgang durch die Ruhelage) gleich der maximalen
potentiellen Energie (am Umkehrpunkt). Bei einem Federpendel ist 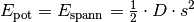 , wobei
, wobei
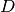 die Federhärte und
die Federhärte und  die Auslenkung bezeichnet. Es gilt also:
die Auslenkung bezeichnet. Es gilt also:
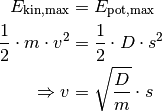
Vergleicht man diesen Zusammenhang mit der Gleichung 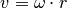 ,
so entspricht der Radius
,
so entspricht der Radius  der Kreisbewegung der Auslenkung
der Kreisbewegung der Auslenkung  aus der Ruhelage. Der Term
aus der Ruhelage. Der Term 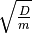 hingegen entspricht der
Winkelgeschwindigkeit
hingegen entspricht der
Winkelgeschwindigkeit  .
.
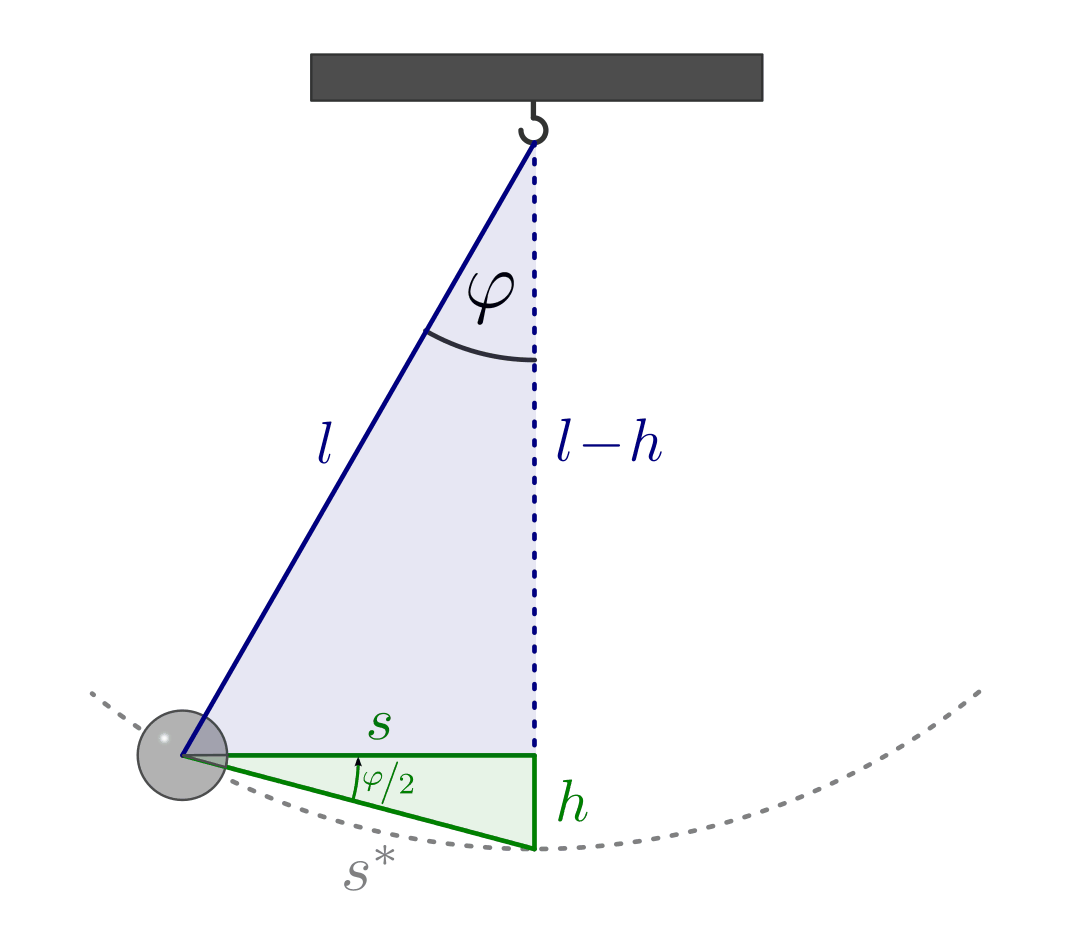
Bei einem Fadenpendel ergeben sich harmonische Schwingungen in guter Näherung
wiederum nur für kleine Winkel, für die die Näherung 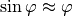 gilt. In diesem Fall können, wie in der obigen Abbildung zu
sehen, zwei Winkelbeziehungen verwendet werden:
gilt. In diesem Fall können, wie in der obigen Abbildung zu
sehen, zwei Winkelbeziehungen verwendet werden:
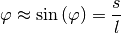
und:
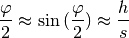
Löst man die zweite Gleichung nach 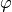 auf, so erhält man
auf, so erhält man
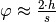 . Dieser Ausdruck kann mit der ersten
Gleichung gleichgesetzt werden. Aufgelöst nach
. Dieser Ausdruck kann mit der ersten
Gleichung gleichgesetzt werden. Aufgelöst nach 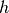 erhält man folgende
Näherung:
erhält man folgende
Näherung:

Setzt man diesen Ausdruck für 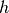 in die Energiegleichung ein, erhält man:
in die Energiegleichung ein, erhält man:
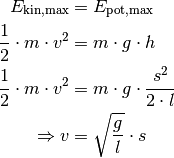
Bei dieser entspricht nun der Term 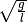 der
Winkelgeschwindigkeit
der
Winkelgeschwindigkeit  ; die Näherung gilt allerdings nur für
kleine Auslenkungen.
; die Näherung gilt allerdings nur für
kleine Auslenkungen.
Zeitliche Änderung von Auslenkung und Geschwindigkeit¶
Sowohl die Auslenkung  wie auch die Geschwindigkeit
wie auch die Geschwindigkeit  haben
bei Schwingungsvorgängen sich periodisch ändernde Werte. Der zeitliche Verlauf
hängt von der Anfangsbedingung ab. Befindet sich ein Pendel zum Zeitpunkt
haben
bei Schwingungsvorgängen sich periodisch ändernde Werte. Der zeitliche Verlauf
hängt von der Anfangsbedingung ab. Befindet sich ein Pendel zum Zeitpunkt
 in der Ruhelage und bewegt sich dabei mit einer Geschwindigkeit
in der Ruhelage und bewegt sich dabei mit einer Geschwindigkeit
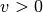 auf einen Umkehrpunkt zu, so kann im Fall einer harmonischen
Schwingung die Auslenkung zu einem beliebigen späteren Zeitpunkt
auf einen Umkehrpunkt zu, so kann im Fall einer harmonischen
Schwingung die Auslenkung zu einem beliebigen späteren Zeitpunkt 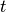 mittels der Sinus-Funktion beschrieben werden:
mittels der Sinus-Funktion beschrieben werden:
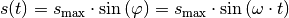
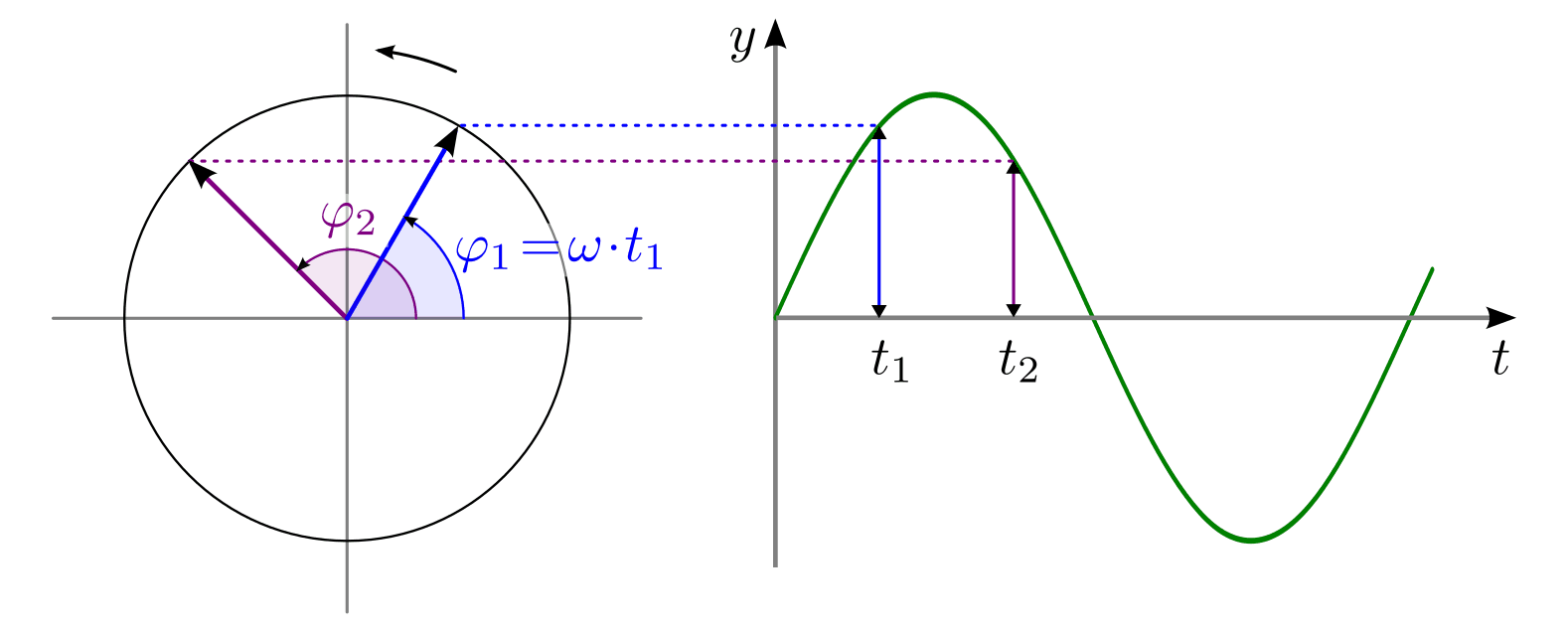
Hierbei ist wiederum die Vorstellung entscheidend, dass jede harmonische
Schwingung mit einer Bewegung eines bestimmten Punktes auf einer Kreisscheibe
verglichen werden kann. Beginnt die Schwingung nicht bei der Ruhelage, sondern
an einem anderen Punkt, so muss zusätzlich eine „Phasenverschiebung“ um einen
Winkel von 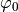 berücksichtigt werden. Es gilt also allgemein:
berücksichtigt werden. Es gilt also allgemein:
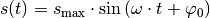
Ist im Speziellen 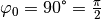 , so ist die
verschobene Sinus-Funktion mit der entsprechenden Cosinus-Funktion identisch:
, so ist die
verschobene Sinus-Funktion mit der entsprechenden Cosinus-Funktion identisch:
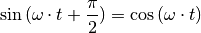
Beginnt die Schwingung also zum Zeitpunkt  an einem Umkehrpunkt und
hat hierbei die Geschwindigkeit
an einem Umkehrpunkt und
hat hierbei die Geschwindigkeit 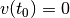 , so ist beispielsweise die
Cosinus-Funktion für die Beschreibung der zeitlichen Änderung der Auslenkung
besser geeignet.
, so ist beispielsweise die
Cosinus-Funktion für die Beschreibung der zeitlichen Änderung der Auslenkung
besser geeignet.
Sowohl die Sinus- wie auch die Cosinus-Funktion haben eine Periode von 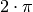 . Löst man die Beziehung
. Löst man die Beziehung 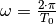 nach
der Schwingungsdauer
nach
der Schwingungsdauer 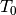 auf, so erhält man für
auf, so erhält man für 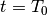 tatsächlich wieder den gleichen Wert wie für
tatsächlich wieder den gleichen Wert wie für  .
.
Beginnt die Schwingung beispielsweise an einem der Umkehrpunkte, so wird nach
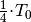 zum ersten mal die Ruhelage durchlaufen. Setzt man
diesen Wert für
zum ersten mal die Ruhelage durchlaufen. Setzt man
diesen Wert für 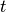 in die Gleichung
in die Gleichung 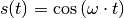 ein, so erhält man wegen
ein, so erhält man wegen 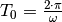 nach
nach
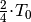 wird der andere Umkehrpunkt erreicht. Nach
wird der andere Umkehrpunkt erreicht. Nach
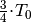 wird zum zweiten Mal die Ruhelage
durchlaufen, bis das Pendel schließlich nach
wird zum zweiten Mal die Ruhelage
durchlaufen, bis das Pendel schließlich nach 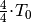 wieder am Ausgangspunkt ankommt.
wieder am Ausgangspunkt ankommt.
In der obigen Abbildung ist der zeitliche Verlauf der Phasenwinkel für ein horizontal schwingenden Pendels als so genanntes „Zeigerdiagramm“ dargestellt. Diese Darstellung ist insbesondere praktisch, um mehrere Schwingungen gleichzeitig darzustellen: Unterschiedliche Zeigerlängen bedeuten verschiedene Amplituden, und unterschiedliche Winkelgeschwindigkeiten bedeuten verschiedene Frequenzen. Die einzelnen Schwingungszustände beziehungsweise Phasen sind zudem am Winkel des jeweiligen Zeigers zu erkennen.
Anmerkungen:
| [1] | Bisweilen wird die Oszillator-Frequenz deshalb auch „Kreisfrequenz“ genannt. Sie gibt an, welche Winkelgeschwindigkeit ein Punkt einer rotierenden Kreisscheibe haben müsste, damit seine Frequenz mit derjenigen des schwingenden Pendelkörpers übereinstimmt. Da die Schwingungsfrequenz
|
| [2] | Für den Auslenkungswinkel sollte 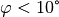 gelten;
dann beträgt der relative Fehler gelten;
dann beträgt der relative Fehler 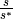 zwischen dem
waagrechten Abstand zwischen dem
waagrechten Abstand 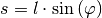 und der Länge des
entsprechenden Kreisbogens und der Länge des
entsprechenden Kreisbogens 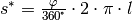 weniger als weniger als 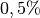 . . |

 des Pendels die Anzahl an
Schwingungsvorgängen je Sekunde angibt, und für eine ganze Umdrehung der
Kreisscheibe ein Winkel von
des Pendels die Anzahl an
Schwingungsvorgängen je Sekunde angibt, und für eine ganze Umdrehung der
Kreisscheibe ein Winkel von 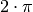 nötig ist, muss die
Kreisfrequenz
nötig ist, muss die
Kreisfrequenz