Ausbreitung von Wärme¶
Ein von selbst ablaufender Austausch von Wärme erfolgt stets von einem Objekt
höherer Temperatur zu einem Objekt niederer Temperatur, bis beide Objekte die
gleiche Temperatur erreicht haben („Wärmegleichgewicht“). Die vom kalten Objekt
aufgenommene Wärmemenge 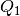 ist hierbei gleich der vom warmen Objekt
abgegebenen Wärmemenge
ist hierbei gleich der vom warmen Objekt
abgegebenen Wärmemenge 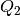 .
.
Die Ausbreitung von Wärme kann auf drei Arten geschehen, die im folgenden Abschnitt näher beschrieben werden.
Die Wärmeleitung¶
Wird Wärme übertragen, obwohl der Körper selbst in Ruhe bleibt, so spricht man von Wärmeleitung. Dabei geben die schnellen Teilchen, aus denen der Körper besteht, ihre Energie allerdings durch Zusammenstöße an benachbarte, langsamere Teilchen ab. So gelangt Wärme von Orten mit hoher Temperatur zu Orten mit tieferer Temperatur.
In Festkörpern breitet sich die Wärme vorwiegend durch Wärmeleitung aus. In Flüssigkeiten und Gasen tritt ebenfalls, jedoch nur in geringem Maße, Wärmeleitung auf. Unterschiedliche Materialien können folglich die Wärme unterschiedlich gut leiten:
Alle Metalle sind gute Wärmeleiter. Allgemein haben alle Materialien, die eine hohe elektrische Leitfähigkeit
 aufweisen, auch eine hohe
Wärmeleitfähigkeit
aufweisen, auch eine hohe
Wärmeleitfähigkeit 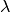 .[1] Der Grund hierfür sind freie
Elektronen, die sowohl elektrische Ladung als auch Wärme transportieren
können.
.[1] Der Grund hierfür sind freie
Elektronen, die sowohl elektrische Ladung als auch Wärme transportieren
können.In der Technik werden Metalle beispielsweise als Kühlkörper an Motoren und Computerchips eingesetzt. In chemischen Laboren werden zur Verwendung von Bunsenbrennern feinmaschige Drahtgitter eingesetzt, um die Flamme nach oben hin zu begrenzen: Das Gitter leitet die Wärme ab, so dass das Gas auf der oberen Seite die Zündtemperatur nicht erreicht.
Glas, Porzellan, Plastik, Schaumstoff und Holz sind schlechte Wärmeleiter. Schaumstoff, Styropor u.s.w. wird in Bauwerken als Isolationsmaterial eingesetzt. Holzgriffe dienen an Werkzeugen und Töpfen als Wärmedämmung.
Flüssigkeiten sind schlechte, Gase sogar sehr schlechte Wärmeleiter. Dünne Luftschichten bis etwa
![\unit[3]{cm}](../_images/math/1b9aa48a4a265214947e8cce5b105572c94d4dd8.png) dienen beispielsweise in
Luftmatratzen als Isolationsschicht. In dickeren Schichten kann Luft
zirkulieren (Wärmeströmung), wodurch die Isolationsfähigkeit erheblich
absinkt.
dienen beispielsweise in
Luftmatratzen als Isolationsschicht. In dickeren Schichten kann Luft
zirkulieren (Wärmeströmung), wodurch die Isolationsfähigkeit erheblich
absinkt.
| Material | 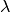 in in 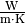 |
| Silber | 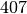 |
| Kupfer | 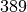 |
| Aluminium | 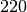 |
| Eisen | 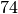 |
| Eis | 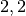 |
| Schaumstoffe, Glas, Porzellan, Beton | 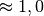 |
| Ziegelstein | 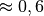 |
| Holz (trocken) | 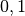 bis bis 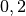 |
| Wasser | 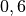 |
| Ethanol | 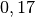 |
| Benzin | 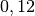 |
| Luft | 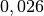 |
Die hohe Wärmedämm-Fähigkeit von Stroh 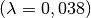 , Styropor
, Styropor
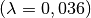 , Kork
, Kork 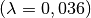 , Mineralwolle
, Mineralwolle
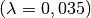 oder Hohlziegeln beruht ebenfalls auf der schlechten
Wärmeleitfähigkeit der eingeschlossenen Luft. Im Vakuum kann überhaupt keine
Wärmeleitung stattfinden.
oder Hohlziegeln beruht ebenfalls auf der schlechten
Wärmeleitfähigkeit der eingeschlossenen Luft. Im Vakuum kann überhaupt keine
Wärmeleitung stattfinden.
Quantitativ lässt sich die Wärmeleitung durch die in einer bestimmten Zeit
transportierte Wärme beschreiben. Für den so genannten Wärmestrom 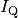 gilt also:
gilt also:
(1)¶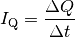
Der Wärmestrom wird in Watt (Joule je Sekunde) gemessen.
Der Wärmestrom 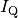 ist einerseits proportional zum
Temperaturunterschied
ist einerseits proportional zum
Temperaturunterschied  zwischen der heißen und der kalten Seite
des Wärmeleiters, andererseits auch proportional zur Wärmeleitfähigkeit
zwischen der heißen und der kalten Seite
des Wärmeleiters, andererseits auch proportional zur Wärmeleitfähigkeit
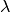 des Wärme leitenden Materials. Zusätzlich ist
des Wärme leitenden Materials. Zusätzlich ist
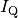 direkt proportional zur Querschnittsfläche
direkt proportional zur Querschnittsfläche 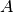 und
indirekt proportional zur Länge beziehungsweise Schichtdicke
und
indirekt proportional zur Länge beziehungsweise Schichtdicke 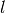 des
Wärmeleiters. Insgesamt gilt also:
des
Wärmeleiters. Insgesamt gilt also:
(2)¶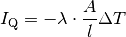
Das Minuszeichen gibt an, dass der Wärmestrom stets in Richtung der kälteren Materialseite stattfindet.[2]
Reihen- und Parallelschaltung von Wärmeleitern
Oftmals besteht ein Wärme leitender Körper, beispielsweise eine Wand mit
Dämmschicht, aus mehr als einem Material. Werden dabei einzelne Schichten mit
gleichen Flächen, aber unterschiedlichen Schichtdicken 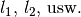 und unterschiedlichen Wärmeleitfähigkeiten
und unterschiedlichen Wärmeleitfähigkeiten 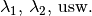 durchlaufen, so handelt es sich um eine
„Reihenschaltung“ mehrerer Wärmeleiter.
durchlaufen, so handelt es sich um eine
„Reihenschaltung“ mehrerer Wärmeleiter.
Um den Wärmestrom in diesem Fall zu berechnen, muss man – wie beim
Ohmschen Gesetz der Elektrizitätslehre – die
„Wärmewiderstände“ der einzelnen Schichten addieren. Dazu definiert man den so
genannten Wärmedurchlasswiderstand 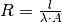 , mit
dem sich die obige Gleichung für den Wärmestrom folgendermaßen formulieren
lässt:[3]
, mit
dem sich die obige Gleichung für den Wärmestrom folgendermaßen formulieren
lässt:[3]
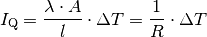
Besteht die Anordnung aus 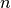 hintereinander liegenden Schichten, so gilt
für
hintereinander liegenden Schichten, so gilt
für 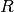 :
:
(3)¶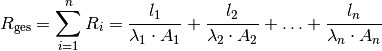
Die Einheit des Wärmewiderstands ist 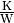 . Bei einer
Reihenschaltung von Wärmewiderständen, beispielsweise einem doppelt verglastem
Fenster oder einer Mauer mit Dämmschicht, sind die Querschnittsflächen der
einzelnen Wärmewiderstände oftmals identisch;
. Bei einer
Reihenschaltung von Wärmewiderständen, beispielsweise einem doppelt verglastem
Fenster oder einer Mauer mit Dämmschicht, sind die Querschnittsflächen der
einzelnen Wärmewiderstände oftmals identisch; 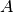 kann in diesem Fall
ausgeklammert werden. Allgemein gilt für den Wärmestrom
kann in diesem Fall
ausgeklammert werden. Allgemein gilt für den Wärmestrom 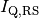 bei einer Reihenschaltung:
bei einer Reihenschaltung:
(4)¶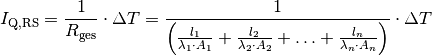
Sind die einzelnen Wärmeleiter nicht hintereinander, sondern nebeneinander angeordnet, so spricht man von einer „Parallelschaltung“ mehrerer Wärmeleiter. In diesem Fall addieren sich die Kehrwerte der Wärmewiderstände zum Kehrwert des Gesamtwiderstands:
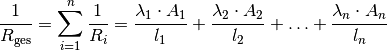
Haben alle parallel zueinander liegenden Wärmeleiter, wie beispielsweise bei
einem Heizkörper oder einem Röhrenkollektor, die gleiche Querschnittsfläche
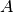 , so kann diese bei der Berechnung des Gesamtwiderstands ausgeklammert
werden. Allgemein gilt für den Wärmestrom
, so kann diese bei der Berechnung des Gesamtwiderstands ausgeklammert
werden. Allgemein gilt für den Wärmestrom 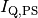 bei einer
Parallelschaltung:
bei einer
Parallelschaltung:
(5)¶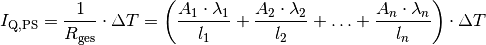
Diese Gleichung kann auch für eine Anordnung mehrerer paralleler Wärmeleiter mit unterschiedlich großen Flächen genutzt werden, beispielsweise einer Außenwand mit einem Fenster oder mehreren Fenstern. Gibt es mehrere Systemgrenzen mit unterschiedlichen Temperaturdifferenzen (beispielsweise Innenwände und Außenwände), so müssen die Wärmeströme durch die einzelnen Bereiche separat berechnet und ihre Werte addiert werden:
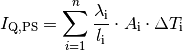
Die Wärmeströmung¶
Strömende Flüssigkeiten und Gase können Wärme mitführen. Diese Art der Wärmeausbreitung, bei der die am Wärmetransport beteiligten Teilchen ihre Lage ändern, wird Wärmeströmung genannt.
Beispiele:
Winde und Meeresströmungen transportieren die Wärme vom Äquator in Richtung der Pole.
In einem Fön wird durch ein Windrad Luft angesaugt und an elektrisch beheizten Heizdrähten vorbei geleitet. So entsteht ein warmer Luftstrom. Mit dem Luftstrom gelangt Wärme an den gewünschten Ort.
Bei einer Warmwasserheizung wird die Wärme durch das Wasser von der Zentralheizung aus in die Heizkörper transportiert.
Eine Vorrichtung zur Strömungserzeugung wie bei einem Fön ist dabei nicht nötig: An der erwärmten Stelle dehnt sich das Wasser aus, seine Dichte nimmt ab. Das erwärmte Wasser steigt deshalb nach oben. Kühleres Wasser strömt von der Seite her nach, so dass sich ein „Kreislauf“ bildet.
Jede Flamme ruft in ihrer Umgebung eine Wärmeströmung hervor. Staub oder andere leichte Körper werden entlang dieser Strömung fort getragen. Durch die Wärmeströmung wird auch ständig frische Luft, die zur Verbrennung notwendig ist, zur Flamme transportiert.
Wärmeströmungen entstehen, weil sich Flüssigkeiten und Gase beim Erwärmen stark ausdehnen und dadurch ihre Dichte verringern. In Vakuum oder ruhenden Körpern kann keine Wärmeströmung stattfinden.
Quantitativ lässt sich die durch Wärmeströmung übertragene Wärmemenge nur
schwer erfassen, da die mathematischen Zusammenhänge bei Strömungsvorgängen sehr
kompliziert sind. In einem vereinfachten Modell kann jedoch angenommen werden,
dass der Wärmestrom 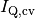 bei auftretender Konvektion
proportional zur Oberfläche
bei auftretender Konvektion
proportional zur Oberfläche 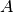 , zum Temperaturunterschied
, zum Temperaturunterschied  zwischen Fluid und begrenzender Kontaktfläche sowie zu einem so genannten
Wärmeübertragungskoeffizienten
zwischen Fluid und begrenzender Kontaktfläche sowie zu einem so genannten
Wärmeübertragungskoeffizienten 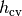 ist:
ist:
(6)¶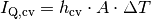
Der Wärmeübertragungskoeffizient 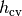 wird in
wird in
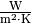 angegeben. Multipliziert man diesen mit der
Temperaturdifferenz
angegeben. Multipliziert man diesen mit der
Temperaturdifferenz  der Kontaktflächen und ihrer Fläche
der Kontaktflächen und ihrer Fläche
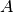 , so erhält man den Wärmestrom beziehungsweise die abgegebene Heizleistung in
Watt. Für technische Anwendungen – beispielsweise in der Bauphysik – sind vor
allem laminare Wärmeströmungen in Luft von Interesse. Für eine horizontal
verlaufende warme Fläche kann hierbei näherungsweise
, so erhält man den Wärmestrom beziehungsweise die abgegebene Heizleistung in
Watt. Für technische Anwendungen – beispielsweise in der Bauphysik – sind vor
allem laminare Wärmeströmungen in Luft von Interesse. Für eine horizontal
verlaufende warme Fläche kann hierbei näherungsweise ![h_{\mathrm{cv}} \approx
\unit[9]{\frac{W}{m^2 \cdot K}}](../_images/math/03f2c84a65e3b347ed3ca1b5da2eeab94e90ad89.png) angenommen werden, für eine vertikale ist
angenommen werden, für eine vertikale ist
![h_{\mathrm{cv}} \approx \unit[5,5]{\frac{W}{m^2 \cdot K}}](../_images/math/555594deab302aac7cd285614d7b6b45ccb946f9.png) .
.
Die Wärmestrahlung¶
Heiße Körper senden stets Wärmestrahlung aus. Durch diese Strahlung kann Wärme ohne Mitwirkung von Materie übertragen werden.
Wärmestrahlung kann Luft durchdringen, ebenso ist sie hinter Fensterscheiben
wahrnehmbar. Die meisten Körper jedoch absorbieren Wärmestrahlung und werden
durch sie erwärmt. Allgemein kann auftreffende Wärmestrahlung von einem Körper
absorbiert, reflektiert, oder durchgelassen werden; Die Summe dieser drei
Anteile ergibt stets 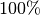 .
.
Beispiele:
- Körper mit dunkler Oberfläche absorbieren einen größeren Teil der Strahlung als Körper mit heller Oberfläche; sie erwärmen sich daher schneller. Der übrige Teil der Strahlung wird reflektiert.
- Glänzende Metalloberflächen reflektieren einen großen Teil der Wärmestrahlung, die restliche Wärmestrahlung wird absorbiert.
- Durchsichtiges Glas absorbiert nur einen kleinen Teil der Wärmestrahlung. Die Wärmestrahlung wird zum Teil reflektiert, zum Teil kann sie das Glas durchdringen. Ebenso erwärmen sich stehende Gewässer durch Sonnenstrahlen nur in der Nähe der Oberfläche; Wärmestrahlung kann dicke Wasserschichten nicht durchdringen.
Quantitativ kann die von einem heißen Gegenstand ausgestrahlte Wärmestrahlung
– ähnlich wie bei den anderen Wärmetransportarten – durch den
Wärmestrom 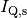 beschrieben werden:
beschrieben werden:
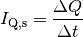
Diese Größe wird bisweilen auch „Bestrahlungsstärke“ genannt, ihre Einheit ist
Watt je Quadratmeter. Beispielsweise kann in Mitteleuropa die Sonne an einem
wolkenlosen Sommertag eine Bestrahlungsstärke von rund
![\unit[1000]{\frac{W}{m^2}}](../_images/math/8b900079c2f26fc8e03a3be29258a2a979f8e2c7.png) erreichen.[4]
erreichen.[4]
Jedes Objekt, das Wärmestrahlung absorbieren kann, emittiert diese auch
entsprechend effizient. Ein idealer „schwarzer Körper“, wie er in der Wärmelehre
oft als vereinfachendes Modell angenommen wird, kann einerseits die auftreffende
Wärmestrahlung zu 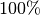 absorbieren und andererseits die seiner
Temperatur entsprechende Wärmestrahlung bestmöglich abstrahlen. Für einen
solchen Körper gilt das nach den Entdeckern Josef Stefan und Ludwig Boltzmann benannte Strahlungsgesetz,
wonach die Intensität der Wärmestrahlung proportional zur vierten Potenz der
absoluten Temperatur (gemessen in Kelvin) ist:
absorbieren und andererseits die seiner
Temperatur entsprechende Wärmestrahlung bestmöglich abstrahlen. Für einen
solchen Körper gilt das nach den Entdeckern Josef Stefan und Ludwig Boltzmann benannte Strahlungsgesetz,
wonach die Intensität der Wärmestrahlung proportional zur vierten Potenz der
absoluten Temperatur (gemessen in Kelvin) ist:
(7)¶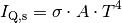
Die dabei auftretende Konstante ![\sigma = \unit[5,670 \cdot
10^{-8}]{\frac{W}{m^2 \cdot K^4}}](../_images/math/c014e4f245e5870b26a79b70116779c8408abfda.png) wird dabei als „Stefan-Boltzmann-Konstante“
bezeichnet. Bei der Wärmestrahlung selbst handelt es sich – wie auch bei Licht
– um elektromagnetische Wellen. Von einem heißen Körper wird allerdings nicht
nur eine einzelne Wellenlänge, sondern vielmehr ein kontinuierliches Spektrum an
unterschiedlichen Wellenlängen abgestrahlt. Die Verteilung der abgestrahlten
Energiemengen bei einer bestimmten Temperatur ist dabei wiederum von der
Wellenlänge
wird dabei als „Stefan-Boltzmann-Konstante“
bezeichnet. Bei der Wärmestrahlung selbst handelt es sich – wie auch bei Licht
– um elektromagnetische Wellen. Von einem heißen Körper wird allerdings nicht
nur eine einzelne Wellenlänge, sondern vielmehr ein kontinuierliches Spektrum an
unterschiedlichen Wellenlängen abgestrahlt. Die Verteilung der abgestrahlten
Energiemengen bei einer bestimmten Temperatur ist dabei wiederum von der
Wellenlänge 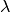 abhängig.
abhängig.
Kann ein Objekt Wärmestrahlung nicht zu 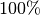 absorbieren oder
emittieren, so muss in der obigen Formel (7) auf
der rechten Gleichungsseite noch ein Zahlenfaktor
absorbieren oder
emittieren, so muss in der obigen Formel (7) auf
der rechten Gleichungsseite noch ein Zahlenfaktor 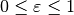 eingefügt werden, der den Emissions- beziehungsweise Absorptionsgrad des
Objekts berücksichtigt:
eingefügt werden, der den Emissions- beziehungsweise Absorptionsgrad des
Objekts berücksichtigt:
(8)¶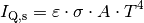
Der Emissions- beziehungsweise Absorptionsgrad  eines Objekts
kann bei unterschiedlichen Wellenlängen unterschiedlich groß sein.
eines Objekts
kann bei unterschiedlichen Wellenlängen unterschiedlich groß sein.
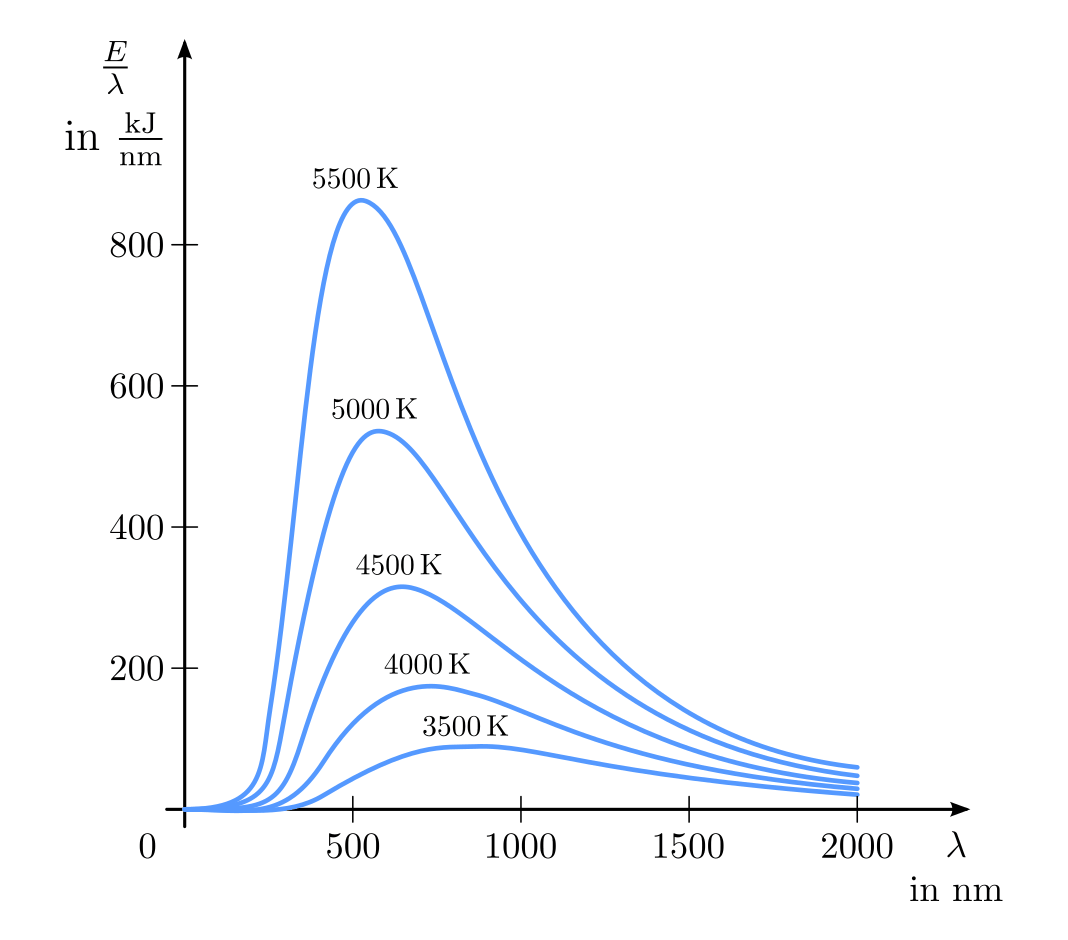
Die spektrale Energiedichte (abgestrahlte Energie je Wellenlänge) der Wärmestrahlung eines schwarzen Körpers bei verschiedenen Temperaturen.
Mit steigender Temperatur verschiebt sich das Spektrum der Strahlung zu kürzeren
Wellenlängen. Während bei geringen Temperaturen die abgestrahlten Wellenlängen
überwiegend im infraroten Bereich liegen, beginnt eine heiße Oberfläche ab einer
Temperatur von mindestens ![T=\unit[700]{\degree C}](../_images/math/846b4f7af474ca136fe9d6a0a6051a59ceec7542.png) (rund
(rund
![\unit[1000]{K}](../_images/math/11b09e55bd6cc8fb5e6ea28bbfff83a4b35415a5.png) ) für das menschliche Auge sichtbar zu glühen. Quantitativ
lässt sich dieser Zusammenhang durch das nach seinem Entdecker Wilhelm Wien benannte „Wiensche
Verschiebungsgesetz“ beschreiben:
) für das menschliche Auge sichtbar zu glühen. Quantitativ
lässt sich dieser Zusammenhang durch das nach seinem Entdecker Wilhelm Wien benannte „Wiensche
Verschiebungsgesetz“ beschreiben:
(9)¶![\lambda_{\mathrm{max}} = \frac{\unit[2897,8]{\mu m \cdot K}}{T}](../_images/math/dbf9587f17b7723971edc2e1f4f51c9de7437bbe.png)
Hierbei beschreibt 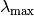 das Maximum der spektralen
Energiedichte bei einer bestimmten (absoluten) Temperatur
das Maximum der spektralen
Energiedichte bei einer bestimmten (absoluten) Temperatur 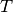 .
Für eine Temperatur von etwa
.
Für eine Temperatur von etwa ![\unit[5800]{K}](../_images/math/c85ec98bd720a9bd7579a0e873cfbe32b70b0771.png) stimmt die Wärmestrahlung
eines schwarzen Körpers in sehr guter Näherung mit dem Strahlungsspektrum der
Sonne überein.
stimmt die Wärmestrahlung
eines schwarzen Körpers in sehr guter Näherung mit dem Strahlungsspektrum der
Sonne überein.
Anmerkungen:
| [1] | Die Proportionalität zwischen Wärmeleitwert 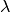 und
elektrischem Leitwert und
elektrischem Leitwert  lässt sich durch die Gleichung lässt sich durch die Gleichung
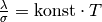 beschreiben. Dieser
Zusammenhang wird nach ihren Entdeckern Gustav Wiedemann und Rudolph
Franz auch als
„Wiedemann-Franzsches Gesetz“ bezeichnet. beschreiben. Dieser
Zusammenhang wird nach ihren Entdeckern Gustav Wiedemann und Rudolph
Franz auch als
„Wiedemann-Franzsches Gesetz“ bezeichnet. |
| [2] | Der Wärmestrom 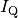 wird von einem Temperaturgefälle wird von einem Temperaturgefälle
 ebenso angetrieben wie ein elektrischer Strom ebenso angetrieben wie ein elektrischer Strom 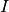 von
einer elektrischen Spannungsdifferenz von
einer elektrischen Spannungsdifferenz 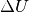 . Die gleiche
Gesetzmäßigkeit gilt außerdem auch bei Diffusionsströmen, die wird
Konzentrationsdifferenzen . Die gleiche
Gesetzmäßigkeit gilt außerdem auch bei Diffusionsströmen, die wird
Konzentrationsdifferenzen 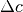 angetrieben werden. angetrieben werden. |
| [3] | Die Analogie zum Ohmschen Gesetz der Elektrizitätslehre besteht darin, dass dieses folgendermassen geschrieben werden kann:
Für die Wärmeleitung gilt:
Die Wärmestrom entspricht somit der elektrischen Stromstärke, nur dass
keine elektrische Ladungsmenge Der elektrische Widerstand kann mittels des spezifischen Widerstands
Verwendet man anstelle des spezifischen Widerstands
Die elektrische Wärmeleitfähigkeit |
| [4] | Außerhalb der Lufthülle der Erde beträgt die Strahlungsintensität der Sonne
im Jahresmitte ![\unit[1367]{\frac{W}{m^2}}](../_images/math/088b1a18fcb5a9e480cef195b40cd3f2dd4d85bd.png) ; diese Größe wird mitunter
auch als „Solarkonstante“ bezeichnet. ; diese Größe wird mitunter
auch als „Solarkonstante“ bezeichnet. |
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.

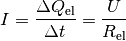
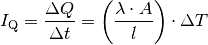
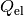 , sondern eine
Wärmemenge (ebenfalls mit
, sondern eine
Wärmemenge (ebenfalls mit 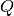 bezeichnet) innerhalb einer bestimmten
Zeit
bezeichnet) innerhalb einer bestimmten
Zeit 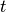 transportiert wird. Die Temperaturdifferenz
transportiert wird. Die Temperaturdifferenz 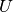 für den elektrischen Stromfluss: Ohne
Temperaturdifferenz gibt es keinen Wärmestrom.
für den elektrischen Stromfluss: Ohne
Temperaturdifferenz gibt es keinen Wärmestrom.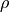 des leitenden Materials ausgedrückt
werden als:
des leitenden Materials ausgedrückt
werden als: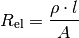
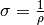 als
materialspezifische Kenngröße, so gilt für den elektrischen Widerstand:
als
materialspezifische Kenngröße, so gilt für den elektrischen Widerstand: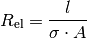
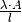 kann somit als Kehrwert des Wärmewiderstands
kann somit als Kehrwert des Wärmewiderstands