Trigonometrie¶
In der Trigonometrie werden Winkelgrößen in Dreiecken untersucht. Diese spielen in vielen Bereichen der Mathematik und Physik eine wichtige Rolle.
Längenverhältnisse im rechtwinkligen Dreieck¶
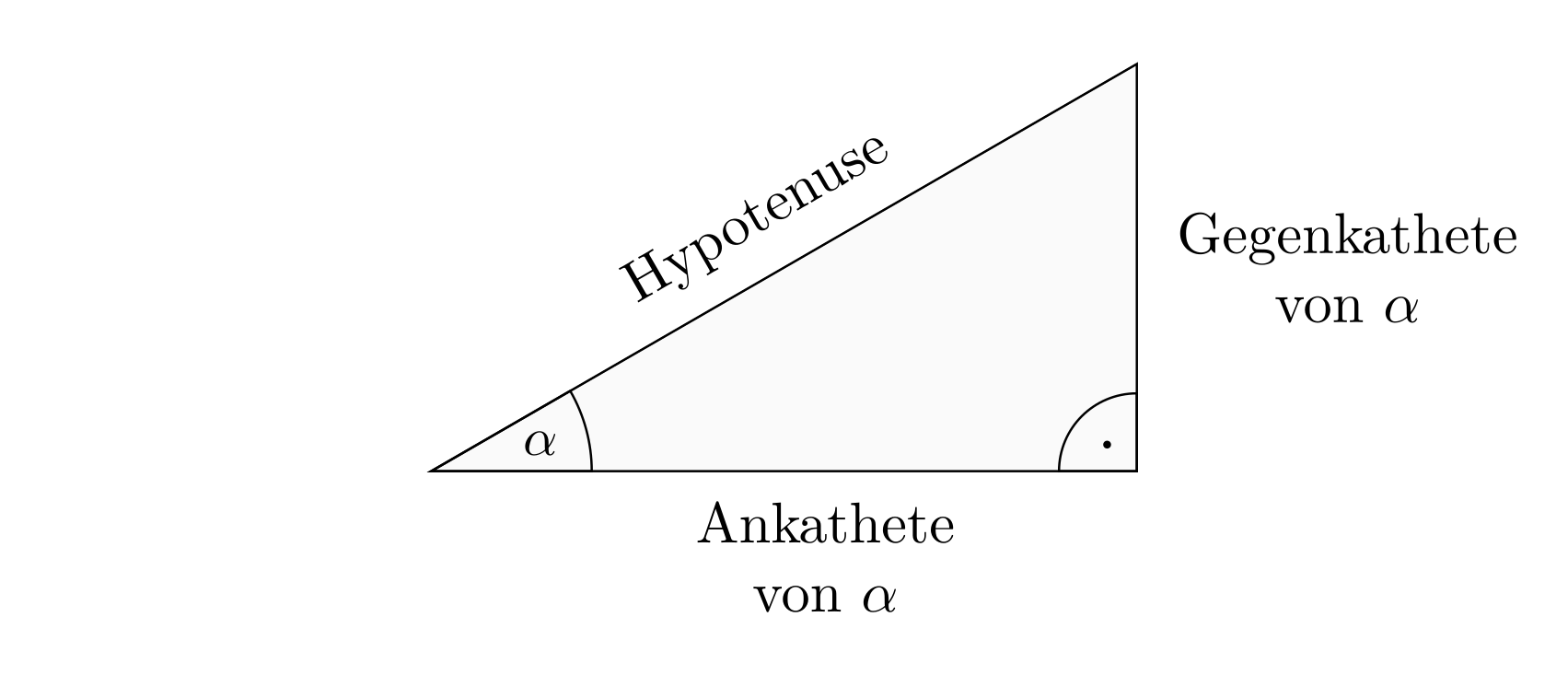
In einem rechtwinkligen Dreieck wird die an dem betrachteten Winkel
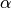 anliegende Kathete als Ankathete, die dem Winkel
anliegende Kathete als Ankathete, die dem Winkel 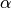 gegenüber liegende Seite als Gegenkathete bezeichnet. Die dem rechten Winkel
gegenüber liegende Seite wird Hypotenuse genannt.
gegenüber liegende Seite als Gegenkathete bezeichnet. Die dem rechten Winkel
gegenüber liegende Seite wird Hypotenuse genannt.
Die Längenverhältnisse der Dreieckseiten lassen sich in Abhängigkeit vom Winkel
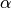 ausdrücken. Hierzu führt man
ausdrücken. Hierzu führt man 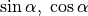 und
und 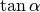 als Kurzschreibweisen für Sinus, Cosinus und Tangens
ein. Diese bezeichnen folgende Seitenverhältnisse:
als Kurzschreibweisen für Sinus, Cosinus und Tangens
ein. Diese bezeichnen folgende Seitenverhältnisse:
(1)¶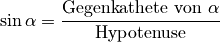
(2)¶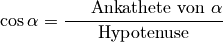
(3)¶
Bisweilen definiert man zusätzlich zum Tangens auch einen so genannten „Cotangens“, der als Kehrwert des Tangens definiert ist:
(4)¶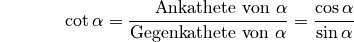
Die Sinus- und Cosinuswerte sind als Längenverhältnis einer Kathete zur
Hypotenuse, da die Hypotenuse die längste Seite im rechtwinkligen Dreieck ist,
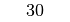
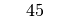
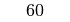
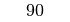
stets kleiner als eins. Die Werte des Tangens können für  alle Werte zwischen
alle Werte zwischen  und
und 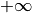 annehmen; für
annehmen; für 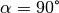 ist der Tangens nicht definiert, da
in diesem Fall durch
ist der Tangens nicht definiert, da
in diesem Fall durch 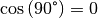 dividiert würde.
dividiert würde.
 |
 |
 |
 |
 |
 |
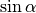 |
 |
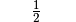 |
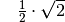 |
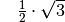 |
 |
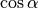 |
 |
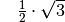 |
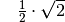 |
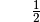 |
 |
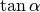 |
 |
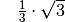 |
 |
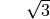 |
 |
Eine weitere Eigenschaft von Sinus und Cosinus ergibt sich daraus, dass der
Sinus des Winkels 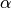 mit dem Cosinus des Winkels
mit dem Cosinus des Winkels 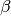 identisch ist. Wegen
identisch ist. Wegen 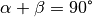 oder
oder 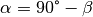 folgt somit:
folgt somit:
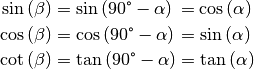
Der Sinus-Satz¶
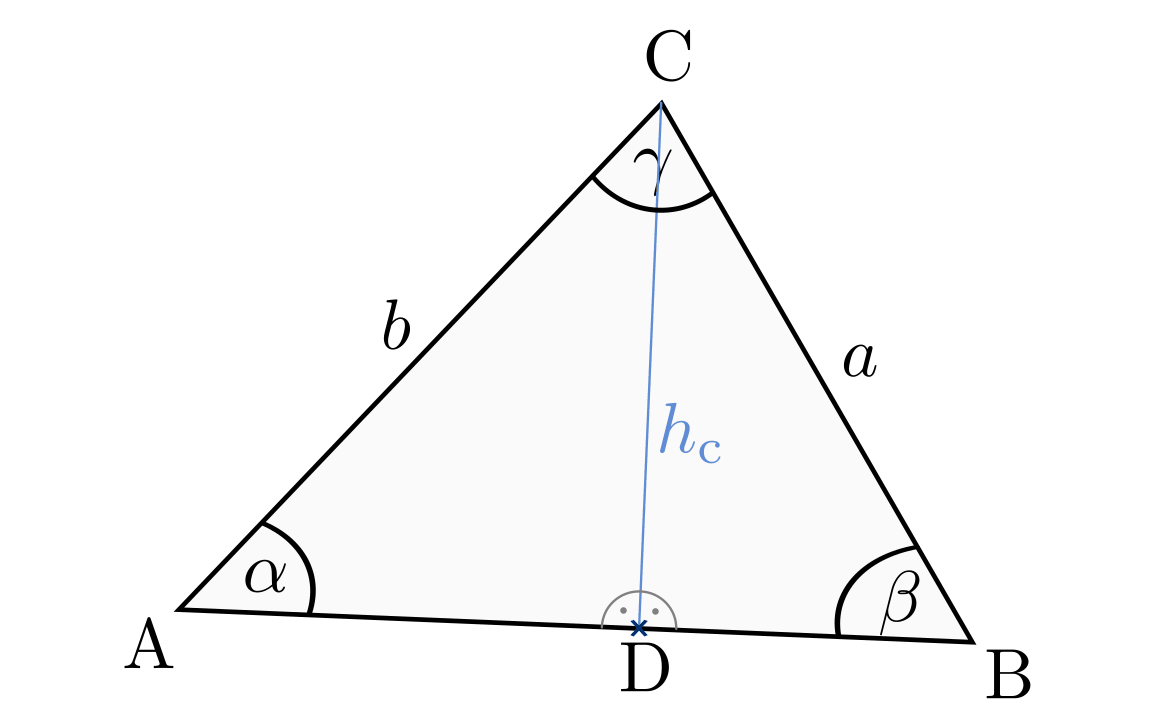
Jedes spitzwinklige Dreieck lässt sich durch Einzeichnen einer Höhenlinie in
zwei rechtwinklige Dreiecke zerlegen. Bezeichnet man den Schnittpunkt der Höhe
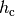 mit der Strecke
mit der Strecke  als
als 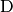 , so gilt
für das Teildreieck
, so gilt
für das Teildreieck 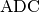 :
:
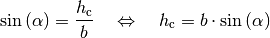
Für das Teildreieck 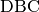 gilt entsprechend:
gilt entsprechend:
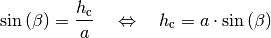
Setzt man die beiden obigen Gleichungen für 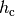 gleich, so erhält man folgende
Beziehung:
gleich, so erhält man folgende
Beziehung:
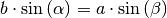
Zeichnet man alle drei Höhenlinien ein, so erhält man jeweils eine entsprechende Größengleichung. Formt man diese in Verhältnisgleichungen um, so ergibt sich der folgende „Sinussatz“:
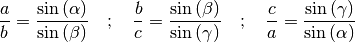
Der Sinussatz wird üblicherweise weiter in eine einzige Gleichung zusammengefasst:
(5)¶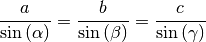
Die Seitenlängen eines Dreiecks stehen also im gleichen Verhältnis zueinander wie die Sinuswerte der jeweils gegenüber liegenden Winkel.
Der Sinus-Satz gilt auch in stumpfwinkligen Dreiecken. Man kann ihn nutzen, um beispielsweise fehlende Stücke eines Dreiecks zu berechnen, wenn zwei Seitenlängen und ein gegenüber liegender Winkel oder eine Seitenlänge und zwei Winkel gegeben sind.
Der Cosinus-Satz¶
In jedem Dreieck ist das Quadrat einer Seitenlänge gleich der Summe der Quadrate der beiden anderen Seitenlängen, abzüglich dem doppelten Produkt aus diesen beiden Seitenlängen und dem Cosinuswert des eingeschlossenen Winkels. Beispielsweise gilt für beliebige Winkelwerte:
(6)¶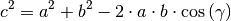
Ist 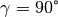 , so ist
, so ist 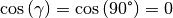 , und damit
, und damit 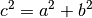 . Der Satz von
Pythagoras ist somit ein Sonderfall des Cosinus-Satzes
für rechtwinklige Dreiecke.
. Der Satz von
Pythagoras ist somit ein Sonderfall des Cosinus-Satzes
für rechtwinklige Dreiecke.
Für die beiden anderen Seiten  und
und  gilt entsprechend:
gilt entsprechend:
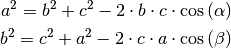
Man kann den Cosinus-Satz zur Konstruktion von Dreiecken nutzen, wenn entweder alle drei Seitenlängen oder zwei Seitenlängen und der von ihnen eingeschlossene Winkel gegeben sind.
Beispiel:
Welche Werte haben die Winkel eines Dreiecks, dessen Seiten
![a=\unit[5]{cm}](../../_images/math/3d330bd6cf1e0fff23006a09af105696c1dd685a.png) ,
, ![b=\unit[6]{cm}](../../_images/math/ac8949f943744d6e136be9032abce94898eea316.png) und
und ![c=\unit[7]{cm}](../../_images/math/0cfdafbc131385f297322f2c050ea9b3b8dff1a8.png) lang
sind?
lang
sind?Nach dem Cosinus-Satz gilt:
![a^2 &= b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos{(\alpha)} \quad
\Leftrightarrow \quad \alpha = \text{acos}\left( \frac{b^2 + c^2 - a^2}{2
\cdot b \cdot c}\right) \\[4pt]
b^2 &= c^2 + a^2 - 2 \cdot c \cdot a \cdot \cos{(\beta)} \quad
\Leftrightarrow \quad \beta = \text{acos}\left( \frac{c^2 + a^2 - b^2}{2
\cdot c \cdot a}\right) \\[4pt]
c^2 &= a^2 + b^2 - 2 \cdot a \cdot b \cdot \cos{(\gamma)} \quad
\Leftrightarrow \quad \gamma = \text{acos}\left( \frac{a^2 + b^2 - c^2}{2
\cdot a \cdot b}\right) \\[4pt]](../../_images/math/ba2a71c3432382d9bd7355790ff627805b9a7ed7.png)
Setzt man die gegebenen Werte ein, so erhält man:
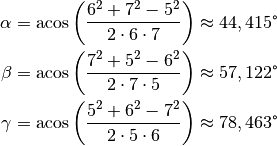
Für die Summe der Innenwinkel gilt erwartungsgemäß
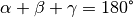 .
.