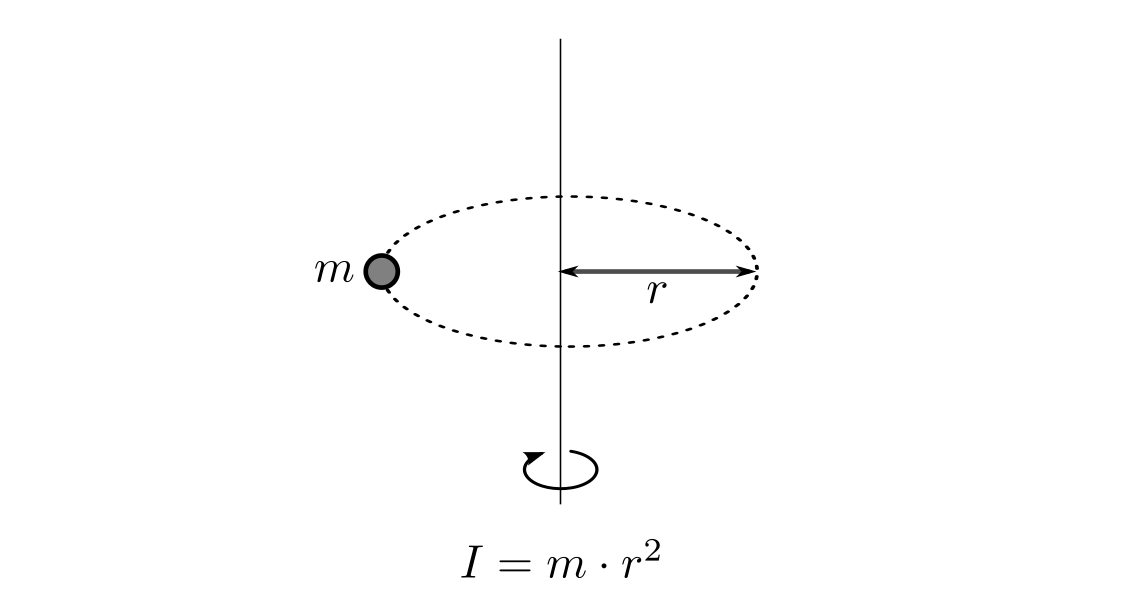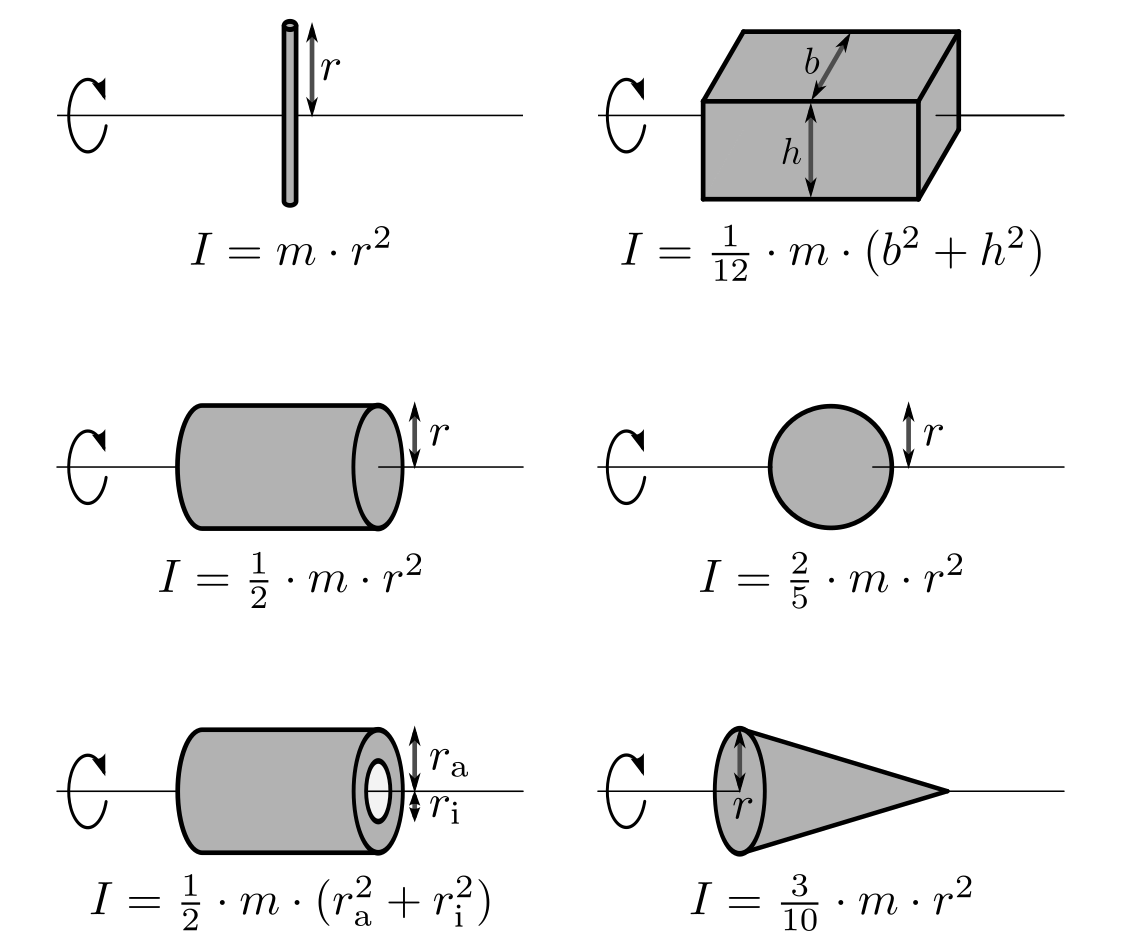Drehmoment und Gleichgewicht¶
Drehmoment¶
Wirkt eine Kraft auf einen starren Körper, so kann sie sowohl eine Verschiebung (Translation ) als auch eine Drehung (Rotation) bewirken. Für die Drehbewegung des Körpers ist dabei nur derjenige Anteil der Kraft von Bedeutung, dessen Wirkungslinie senkrecht zur Linie zwischen Drehachse und Angriffspunkt der Kraft steht.
Definition:
Wirkt eine Kraft
im senkrechten Abstand
von einer festen Drehachse, so erzeugt sie ein Drehmoment
, für das gilt:
Hierbei bezeichnet
den Winkel zwischen der Kraftrichtung und der Verbindungslinie vom Drehzentrum zum Angriffspunkt der Kraft.
Das Drehmoment ist als Vektorprodukt seinem Betrag nach maximal, wenn die Kraft
senkrecht zur Strecke
zwischen Angriffspunkt und Drehachse auf den Körper einwirkt. Wirkt die Kraft entlang dieser Verbindungslinie, so ist der Betrag des Drehmoments gleich Null.
Einheit:
Die Einheit des Drehmoments ist – gemäß seiner Definition – das Newtonmeter. Ein Newtonmeter entspricht demjenigen Drehmoment, das eine Kraft
im senkrechten Abstand
ihrer Wirkungslinie von der Drehachse erzeugt.
Das Kräftepaar
Ein Sonderfall eines Drehmoments tritt auf, wenn zwei gleich große, aber in
entgegengesetzter Richtung wirkende Kräfte am gleichen Gegenstand angreifen.
Bezeichnet man mit 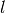 den Abstand der zwei zueinander parallelen
Wirkungslinien beider Kräfte
den Abstand der zwei zueinander parallelen
Wirkungslinien beider Kräfte 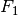 und
und 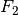 , so gilt für die
resultierenden Drehmomente
, so gilt für die
resultierenden Drehmomente 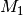 und
und 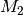 :
:
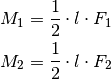
Damit ergibt sich als Drehmoment insgesamt:
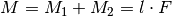
Das Drehmoment derartiger Kräftepaare ist beispielsweise für Schrauben, Windeisen, Kreuzschlüssel usw. von Bedeutung.
Gleichgewicht¶
Ein um eine Achse drehbarer Körper ist im Gleichgewicht, wenn sich alle an ihm wirkenden Drehmomente gegenseitig ausgleichen.
Definition:
Der Schwerpunkt ist der Punkt eines starren Körpers, bei dem sich alle durch sein Gewicht wirkenden Drehmomente
zu Null addieren:
Die Kräfte
entsprechen dabei den Gewichtskräften der einzelnen fest miteinander verbundenen Massestücke („Massenpunkte“).[1] Die Strecken
den zugehörigen Abständen vom Schwerpunkt, sofern dieser als Koordinatenursprung angesehen wird.
Ist ein anderes Koordinatensystem vorgegeben, so gilt für den Schwerpunkt
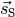 eines Körpers:
eines Körpers:
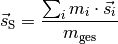
Hierbei werden mit 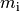 die Massen der einzelnen Punktmassen und
mit
die Massen der einzelnen Punktmassen und
mit 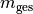 die Gesamtmasse bezeichnet.
die Gesamtmasse bezeichnet.
Ist die Summe aller wirkenden Drehmomente bezüglich einem bestimmten Punkt als feste Drehachse nicht gleich Null, so führt der Körper eine Rotation um diese Drehachse aus.
Stabiles, labiles und indifferentes Gleichgewicht
Allgemein kann zwischen drei unterschiedlichen Gleichgewichts-Arten unterschieden werden:
- Ein Körper im stabilen Gleichgewicht kehrt bei einer kleinen Auslenkung von selbst wieder in seine ursprüngliche Lage zurückführt.
- Ein Körper im labilen Gleichgewicht kippt bei einer minimalen Auslenkung um, entfernt sich also dauerhaft von der Ausgangslage.
- Ein Körper in indifferentem Gleichgewicht ist in keiner Lage stabiler als in einer anderen. Dies gilt beispielsweise für Kugeln, Walzen oder Räder.
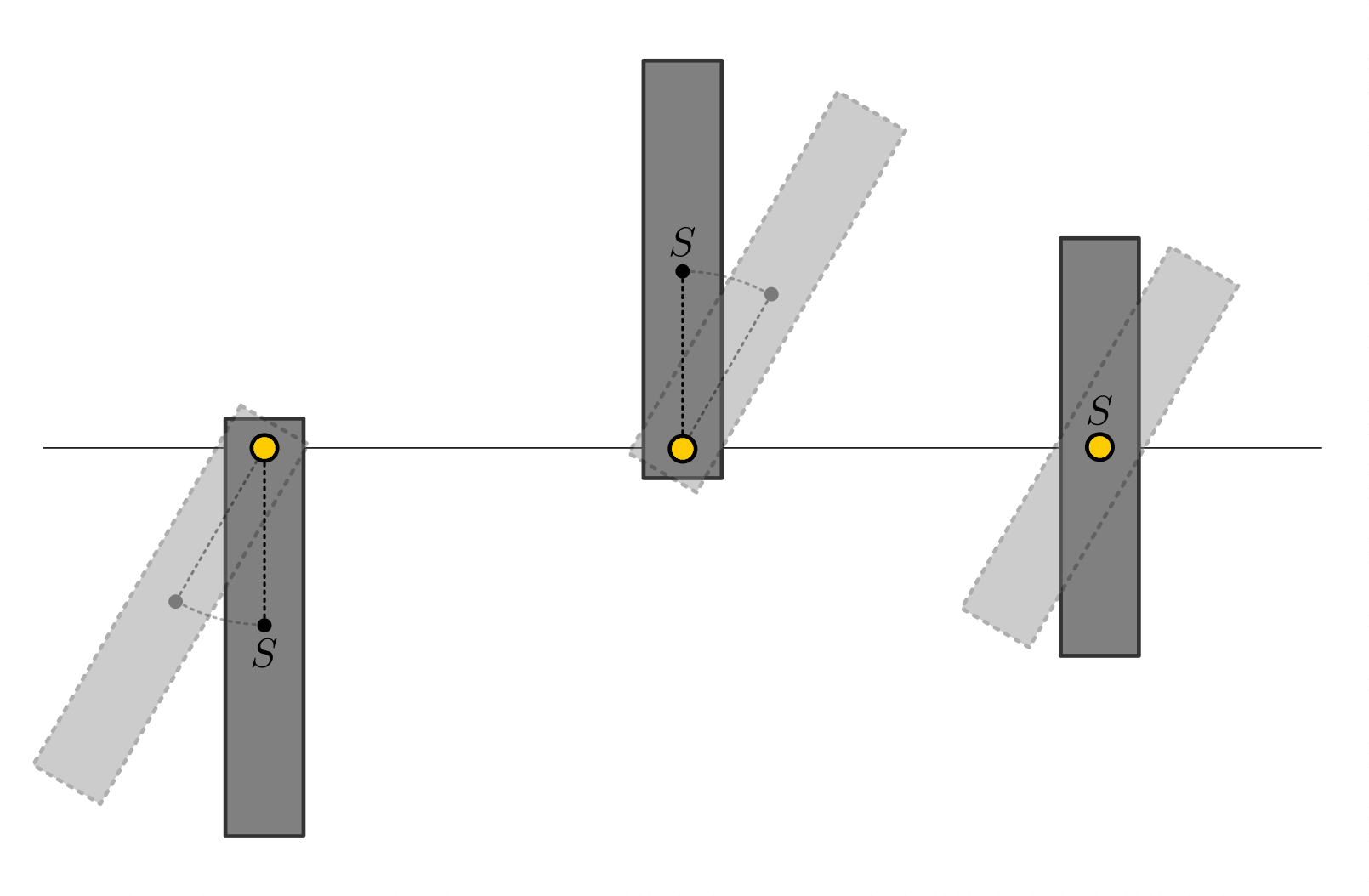
Kann sich ein Körper frei um eine Drehachse beziehungsweise einen Aufhängepunkt drehen, so nimmt sein Schwerpunkt die tiefst mögliche Stelle ein. In dieser Lage befindet sich der Schwerpunkt stets senkrecht unterhalb der Achse beziehungsweise des Aufhängepunktes. Sind Schwerpunkt, Aufhänge- und Drehpunkt identisch, so befindet sich der Körper in jeder Lage im indifferenten Gleichgewicht.
Schwerpunkt und Auflagefläche¶
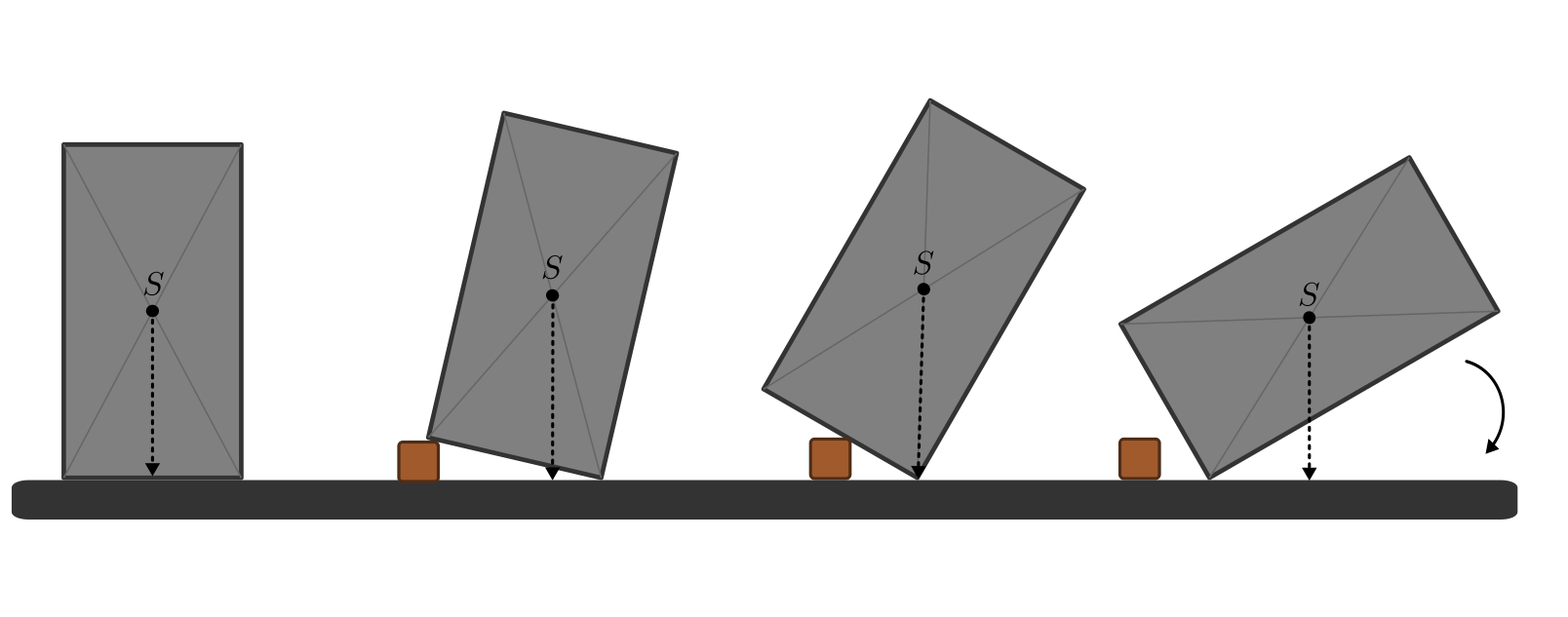
Ein frei stehender Körper, an dem keine äußeren Drehmomente wirken, kippt nicht um, solange sich sein Schwerpunkt oberhalb der Auflagefläche („Standfläche“) befindet. Der Grund dafür ist, dass bei einer kleinen Auslenkung der Schwerpunkt des Körpers zunächst angehoben wird.
Bei einer weiteren Auslenkung überschreitet die vom Schwerpunkt aus senkrecht nach unten gezeichnete Lot-Linie die Grenze der Auflagefläche. Sobald dies der Fall ist, kippt der Körper um und nimmt damit eine stabile Gleichgewichtslage mit tiefer liegendem Schwerpunkt ein.
Hat ein Gegenstand oder Körper mehrere Auflagepunkte, so entspricht die Auflagefläche der Fläche zwischen den einzelnen Auflagepunkten. Beispielsweise entspricht die Auflagefläche eines Schemels mit drei Beinen der dreieckigen Fläche, die von den Beinen des Schemels begrenzt wird.
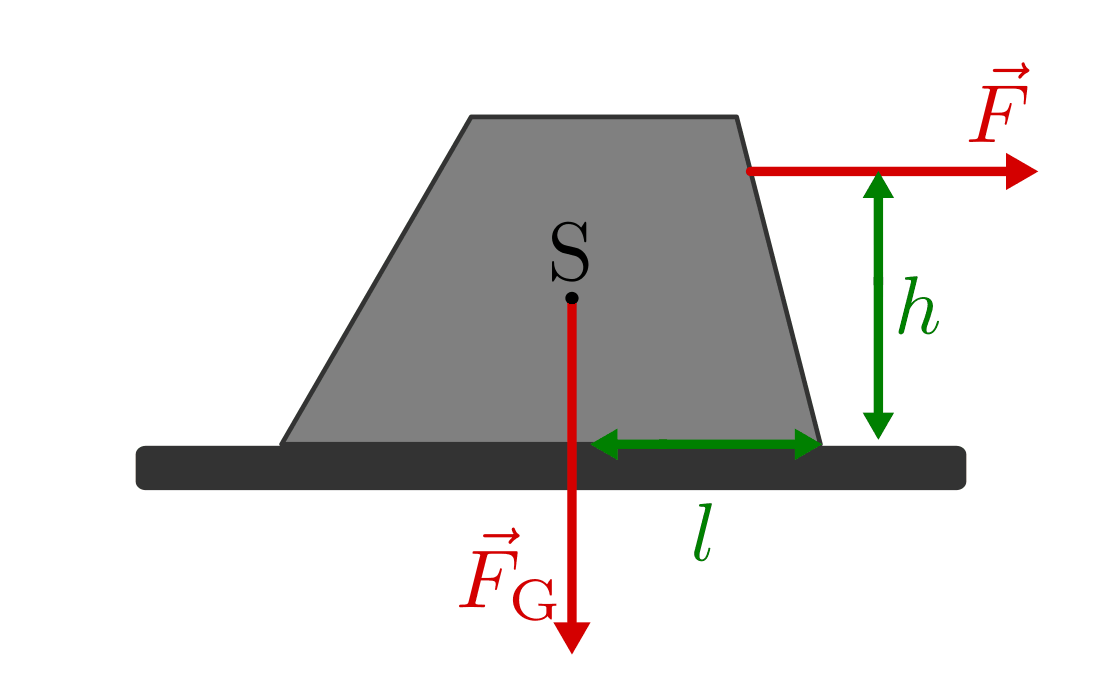
Wirkt eine Kraft 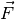 in einer Höhe
in einer Höhe 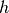 über der Standfläche
waagrecht auf den Körper ein, so übt diese bezüglich der Kippkante ein so
genanntes Kippmoment
über der Standfläche
waagrecht auf den Körper ein, so übt diese bezüglich der Kippkante ein so
genanntes Kippmoment 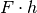 aus. Im entgegengesetzten Drehsinn
bewirkt die im Schwerpunkt
aus. Im entgegengesetzten Drehsinn
bewirkt die im Schwerpunkt 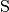 wirkende Gewichtskraft des Gegenstands
ein „Standmoment“
wirkende Gewichtskraft des Gegenstands
ein „Standmoment“ 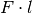 , wobei
, wobei 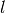 den Abstand der Kippkante
von der Wirkungslinie der Gewichtskraft angibt. Im Gleichgewichtsfall gilt:
den Abstand der Kippkante
von der Wirkungslinie der Gewichtskraft angibt. Im Gleichgewichtsfall gilt:
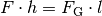
Die zum Kippen des Gegenstands nötige Kraft beträgt also mindestens:
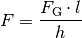
Die Standfestigkeit eines Gegenstands ist umso größer, je geringer seine Höhe
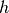 ist, je größer seine Gewichtskraft
ist, je größer seine Gewichtskraft 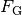 ist und je
größer der senkrechte Abstand
ist und je
größer der senkrechte Abstand 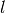 des Schwerpunkts zur Kippkante ist.[2]
des Schwerpunkts zur Kippkante ist.[2]
Das Trägheitsmoment¶
Wird ein Gegenstand durch ein äußeres Drehmoment so weit gekippt, dass sein Gleichgewicht einen instabilen Zustand annimmt, so beginnt dieser eine Rotationsbewegung auszuführen.
Bei Translationsbewegungen ist die Beschleunigung 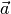 , die ein
Körper durch eine äußere Kraft
, die ein
Körper durch eine äußere Kraft 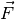 erfährt, umgekehrt proportional
zur Masse
erfährt, umgekehrt proportional
zur Masse 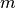 des Körpers („Kraftgesetz“). Entsprechend ist bei
Rotationsbewegungen die Winkelbeschleunigung
des Körpers („Kraftgesetz“). Entsprechend ist bei
Rotationsbewegungen die Winkelbeschleunigung 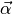 , die ein Körper durch ein
äußeres Drehmoment
, die ein Körper durch ein
äußeres Drehmoment 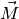 erfährt, umgekehrt proportional zum
sogenannten Trägheitsmoment
erfährt, umgekehrt proportional zum
sogenannten Trägheitsmoment 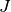 des Körpers.
des Körpers.
Es gilt also:
Für Translationsbewegungen:
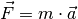
Für Rotationsbewegungen:
(1)¶
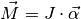
Das Drehmoment zeigt in die gleiche Richtung wie die Winkelbeschleunigung, zeigt
also in Richtung der Drehachse; der Betrag des Drehmomentvektors ist um den
Faktor 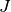 vom Betrag der Winkelbeschleunigung
vom Betrag der Winkelbeschleunigung 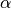 verschieden.
verschieden.
Der Wert des Trägheitsmoment 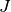 eines Körpers hängt einerseits von der Lage der
Drehachse, andererseits von der räumlicher Verteilung der rotierenden Masse ab.
Massestücke, die weit von der Drehachse entfernt liegen, tragen stärker zum
Trägheitsmoment bei als Massestücke, die sich in der Nähe der Drehachse
befinden. Beispielsweise hat ein kleines Teilchen der Masse
eines Körpers hängt einerseits von der Lage der
Drehachse, andererseits von der räumlicher Verteilung der rotierenden Masse ab.
Massestücke, die weit von der Drehachse entfernt liegen, tragen stärker zum
Trägheitsmoment bei als Massestücke, die sich in der Nähe der Drehachse
befinden. Beispielsweise hat ein kleines Teilchen der Masse 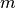 , das auf
einer Kreisbahn mit Radius
, das auf
einer Kreisbahn mit Radius  rotiert, ein Trägheitsmoment von
rotiert, ein Trägheitsmoment von 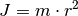 .
.
Das Trägheitsmoment eines beliebig geformten Körpers kann rechnerisch bestimmt
werden, wenn man ihn aus einer Vielzahl von einzelnen kleinen Massestücken
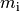 zusammengesetzt denkt, die jeweils im Abstand
zusammengesetzt denkt, die jeweils im Abstand
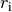 von der Drehachse entfernt liegen. Das Trägheitsmoment
des Körpers ist dann gleich der Summe der Trägheitsmomente aller einzelnen
Teilstücke:
von der Drehachse entfernt liegen. Das Trägheitsmoment
des Körpers ist dann gleich der Summe der Trägheitsmomente aller einzelnen
Teilstücke:
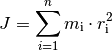
Die Trägheitsmomente einiger regelmäßig geformter Körper, die in technischen Anwendungen häufig auftreten, sind in Formelsammlungen aufgelistet. Eine kleine Auswahl davon findet sich in Abbildung Trägheitsmomente. Dabei ist zu beachten, dass der gleiche Körper bezüglich unterschiedlichen Rotationsachsen verschiedene Trägheitsmomente besitzen kann.
Der Satz von Steiner
Rotiert ein Körper mit einer Masse 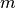 um eine Achse, die im Abstand
um eine Achse, die im Abstand
 parallel zum Schwerpunkt verläuft, so muss zum jeweiligen Wert
parallel zum Schwerpunkt verläuft, so muss zum jeweiligen Wert
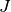 des Trägheitsmoments noch der Term
des Trägheitsmoments noch der Term 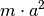 hinzu addiert
werden. Das lässt sich dadurch erklären, dass in diesem Fall der Schwerpunkt
des Körpers auf einer Kreisbahn um die neue Drehachse rotiert. Es gilt somit:
hinzu addiert
werden. Das lässt sich dadurch erklären, dass in diesem Fall der Schwerpunkt
des Körpers auf einer Kreisbahn um die neue Drehachse rotiert. Es gilt somit:
(2)¶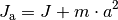
Formal ist das neue Trägheitsmoment also gleich dem ursprünglichen Trägheitsmoment (bei Rotation um den Schwerpunkt) plus dem Trägheitsmoment des Schwerpunkts um die neue Rotationsachse. Somit lassen sich viele Rotationsvorgänge (insbesondere Rollbewegungen) in einfacher Weise auf Drehbewegungen um den Schwerpunkt zurückführen.
Experimentelle Bestimmung des Trägheitsmoments
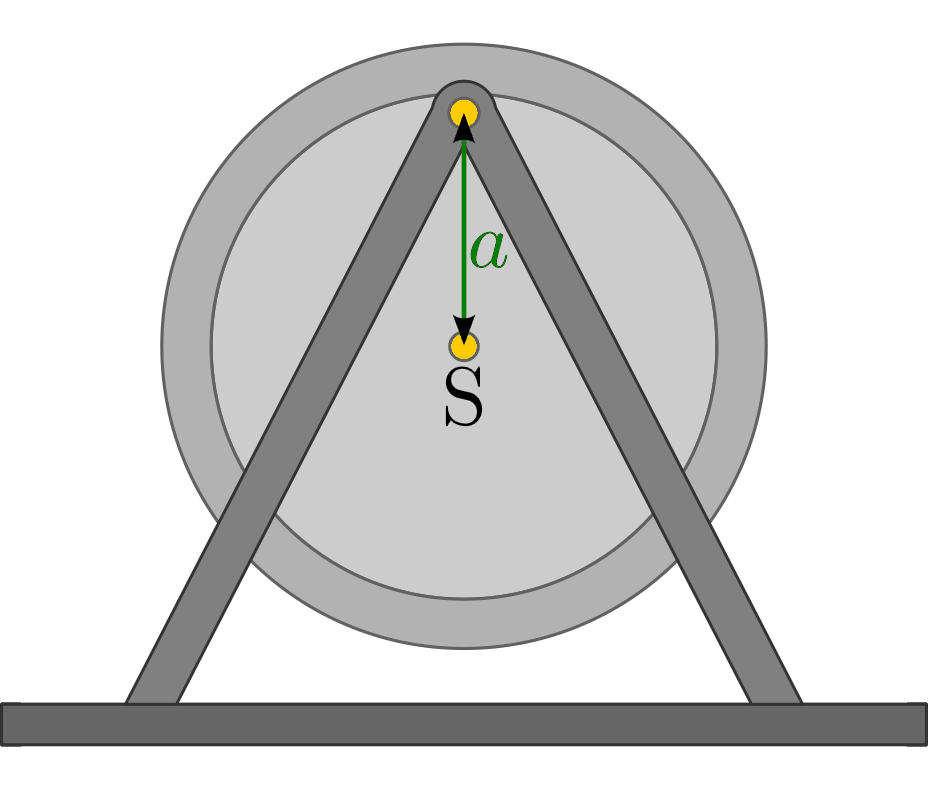
Um das Trägheitsmoment eines beliebigen Objekts, beispielsweise einer rotierenden Scheibe oder eines Rades, experimentell zu bestimmen, kann man es beispielsweise mittels einer Halterung oberhalb seines Schwerpunkts frei drehbar aufhängen.
Lenkt man diese Anordnung aus der Ruhelage aus, so beginnt es als
physikalisches Pendel mit einer leicht messbaren
Schwingungsdauer 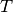 um die Ruhelage zu schwingen. Für das Trägheitsmoment
des Objekts um seinen Schwerpunkt gilt dann:
um die Ruhelage zu schwingen. Für das Trägheitsmoment
des Objekts um seinen Schwerpunkt gilt dann:
(3)¶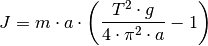
Hierbei bezeichnet ![g = \unit[9,81]{\frac{m}{s^2}}](../_images/math/c64dddb2fc70d09e440b703a0826e8a4dc996987.png) die Erdbeschleunigung,
die Erdbeschleunigung,
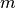 die Masse des schwingenden Gegenstands, und
die Masse des schwingenden Gegenstands, und  den Abstand
zwischen seinem Schwerpunkt
den Abstand
zwischen seinem Schwerpunkt 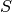 und dem Aufhängepunkt. Da alle anderen
Größen in der obigen Formel entweder konstant oder ebenfalls leicht messbar
sind, kann das Trägheitsmoment unmittelbar bestimmt werden.
und dem Aufhängepunkt. Da alle anderen
Größen in der obigen Formel entweder konstant oder ebenfalls leicht messbar
sind, kann das Trägheitsmoment unmittelbar bestimmt werden.
Anmerkungen:
| [1] | Der Begriff „Massenpunkt“ bezieht sich auf einen physikalischen Körper, dessen Verhalten hinreichend beschrieben werden kann, wenn man sich dessen gesamte Masse in seinem Schwerpunkt vereinigt denkt. Beispielsweise kann eine Hantelstange mit zwei außen angebrachten Gewichten gleicher Masse und Form in guter Näherung als ein starrer Körper aufgefasst werden, der aus zwei fest miteinander verbundenen Punktmassen besteht. Der Schwerpunkt liegt in diesem Fall mittig in der Hantelstange. |
| [2] | Liegt der Schwerpunkt durch eine unterschiedliche Massenverteilung nicht in der Mitte, sondern im unteren Teil des Gegenstands, so muss zudem eine größere Hubarbeit geleistet werden, um den Schwerpunkt über die Kippkante zu heben – zum Kippen ist in diesem Fall also mehr Arbeit nötig. |
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.