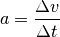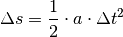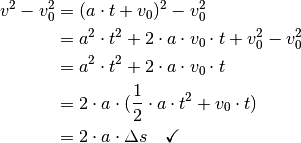Bewegungen mit konstanter Beschleunigung¶
Das Modell einer Bewegung mit konstanter Beschleunigung stellt eine Verallgemeinerung einer Bewegung mit konstanter Geschwindigkeit dar. Hat ein sich bewegendes Objekt insbesondere eine konstante Beschleunigung mit einem Wert von Null, so bewegt es sich mit konstanter Geschwindigkeit fort; Eine Bewegung mit konstanter Gschwindigkeit kann also Spezialfall einer beschleunigten Bewegung angesehen werden.
Durch das Einbeziehen von Beschleunigungen wird berücksichtigt, dass keine abrupten, sondern stets nur kontinuierliche Geschwindigkeitsänderungen möglich sind. Die allgemeinen Zusammenhänge zwischen Geschwindigkeitsänderung, Beschleunigung und Zeit beziehungsweise Wegstrecke werden im folgenden Abschnitt zunächst für geradlinige, dann auch für zusammengesetzte Bewegungsvorgänge näher beschrieben.
Eindimensionale Bewegungen mit konstanter Beschleunigung¶
Bei einer Bewegung mit konstanter Beschleunigung nimmt die Geschwindigkeit eines Objekts in gleichen Zeitabschnitten um den jeweils gleichen Betrag zu beziehungsweise ab.
Definition:
Die Beschleunigung
eines sich geradlinig bewegenden Objekts ist gleich dem Verhältnis aus der Geschwindigkeitsänderung
und der dazu benötigten Zeit
:
(1)¶
Einheit:
Die Beschleunigung wird in Meter je Quadratsekundeangegeben.
Beispiele:
![\unitfrac[1]{m}{s^2}](../../_images/math/88f3123d957be49d5f8662c23aa9fde8b2c52c26.png) ist die Beschleunigung eines Objekts, dessen
Geschwindigkeit sich in
ist die Beschleunigung eines Objekts, dessen
Geschwindigkeit sich in ![\unit[1]{s}](../../_images/math/a69295d00e6b71b7e4e11080041344fe1df0e00c.png) um
um ![\unitfrac[1]{m}{s}](../../_images/math/d5c0e197189d15181ca081ac6346c0f677b670b4.png) ändert.
ändert.- Ein Fahrzeug, das in einer Zeit von
![t=\unit[10]{s}](../../_images/math/6935b8e2ad5c3998c992b4f031934b2d2b68e4e9.png) von
von
![\unitfrac[0]{km}{h}](../../_images/math/8f097ca03046a58df8eb5738626867b9b87ffa5f.png) auf
auf ![\unitfrac[100]{km}{h} =
\unitfrac[27,8]{m}{s}](../../_images/math/1a3592b16b51e959a34c079f50a4ba3eeb52d99b.png) angetrieben wird, weist eine Beschleunigung von
angetrieben wird, weist eine Beschleunigung von
![\unitfrac[2,78]{m}{s^2}](../../_images/math/f15c999dda60fab8898e009dd2cc1ee2fe1d4129.png) auf.
auf.
- Die Beschleunigung die ein Objekt im freier Fall auf der Erde erfährt
(„Erdbeschleunigung“), beträgt rund
![\unitfrac[9,81]{m}{s^2}](../../_images/math/59f11f578e48f622fe99a9e424739677e0b4761e.png) . Häufig
wird diese Beschleunigung, die bei vielerlei physikalischen Vorgängen eine
Rolle spielt, mit dem Buchstaben
. Häufig
wird diese Beschleunigung, die bei vielerlei physikalischen Vorgängen eine
Rolle spielt, mit dem Buchstaben ![g=\unitfrac[9,81]{m}{s^2}](../../_images/math/4c1f726a3c213fe4ea947b680beaf5a4d2931c6d.png) bezeichnet und Ortsfaktor genannt.
bezeichnet und Ortsfaktor genannt.
Bei längeren Bewegungsvorgängen können aufeinander folgende Zeitabschnitte unterschiedliche Beschleunigungen aufweisen. Beispielsweise beschleunigt ein Sprinter zunächst gleichmäßig, bis er seine Höchstgeschwindigkeit erreicht hat, hält diese Geschwindigkeit (möglichst) konstant bis zum Ziel, und bremst nach der Ziellinie wieder gleichmäßig ab. Derartige Bewegungsvorgänge lassen sich oftmals abschnittsweise durch jeweils konstante (Durchschnitts-)Beschleunigungen beschreiben.
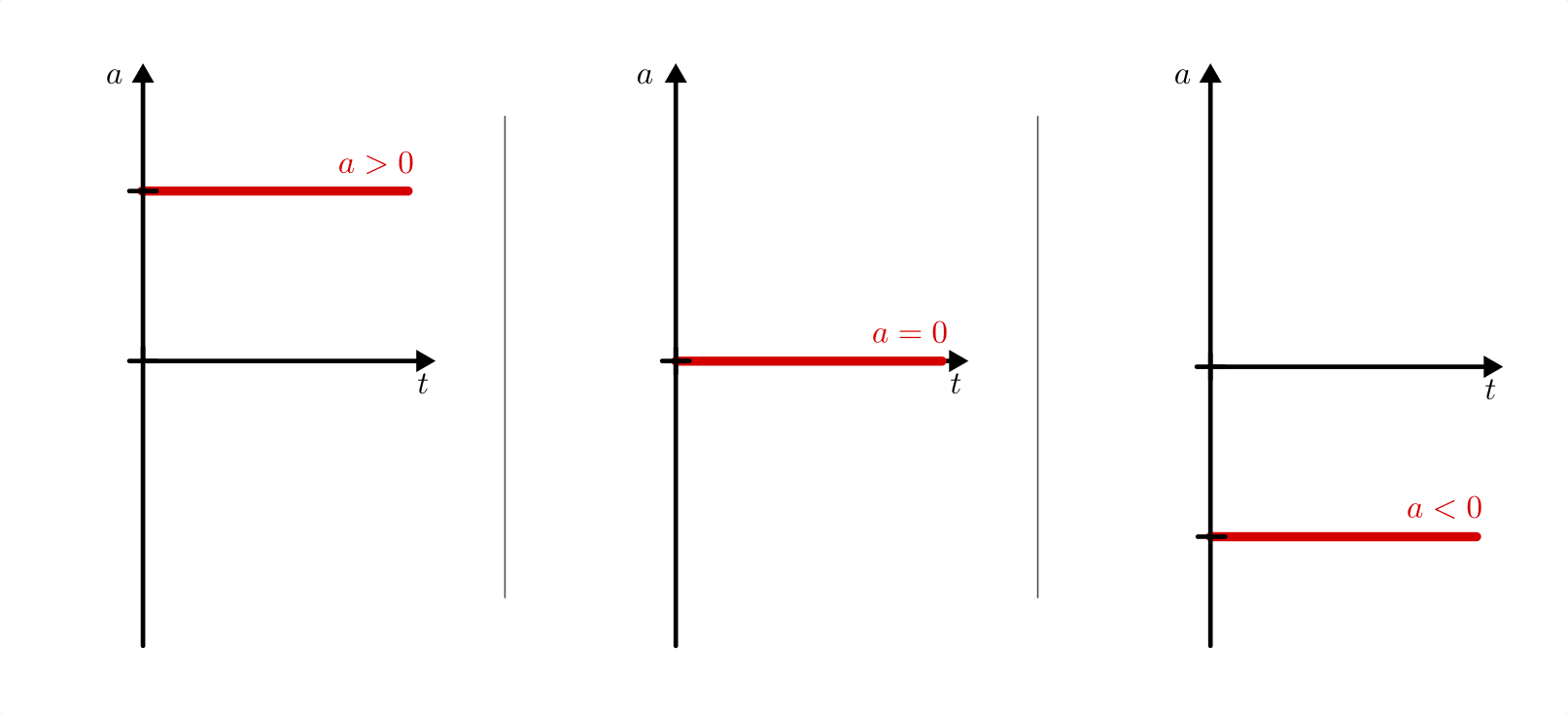
Beschleunigung-Zeit-Diagramme einer konstanten Beschleunigung. Der Wert der Beschleunigung kann größer, gleich oder kleiner Null sein.
Beschleunigung und Geschwindigkeit
Aus Gleichung (1) folgt, dass sich die
Geschwindigkeit bei einer konstanten Beschleunigung  in gleichen
Zeitabschnitten
in gleichen
Zeitabschnitten 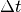 kontinuierlich um den Wert
kontinuierlich um den Wert 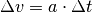 verändert.
verändert.
Kennt man die (konstante) Beschleunigung  eines Objekts und weiß, über
welchen Zeitabschnitt
eines Objekts und weiß, über
welchen Zeitabschnitt 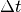 die Beschleunigung anhält, so kann man im
Allgemeinen jedoch nicht angeben, wie groß die Geschwindigkeit
die Beschleunigung anhält, so kann man im
Allgemeinen jedoch nicht angeben, wie groß die Geschwindigkeit  des
Objekt zur Zeit
des
Objekt zur Zeit 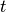 ist. Hierzu muss man zusätzlich wissen, wie groß die
anfängliche Geschwindigkeit
ist. Hierzu muss man zusätzlich wissen, wie groß die
anfängliche Geschwindigkeit 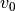 des Objekts war. Für den zeitlichen
Verlauf der Geschwindigkeit
des Objekts war. Für den zeitlichen
Verlauf der Geschwindigkeit 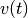 gilt also:
gilt also:
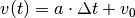
Zeichnet man ein 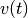 -Diagramm einer solchen Bewegung, so entspricht der
Graph der Geschwindigkeit einer Geraden.
-Diagramm einer solchen Bewegung, so entspricht der
Graph der Geschwindigkeit einer Geraden.
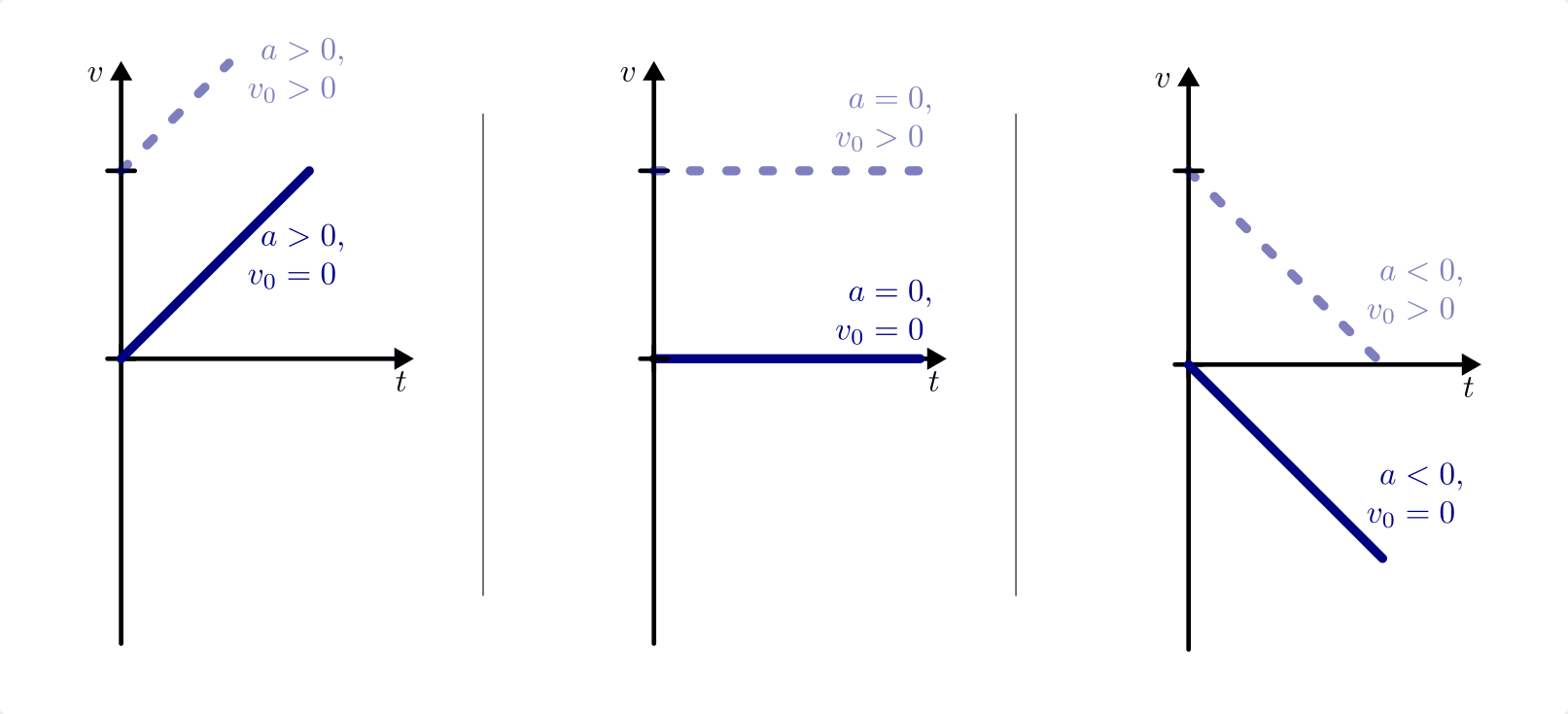
Geschwindigkeit-Zeit-Diagramme einer konstanten Beschleunigung. Die Steigung der Geschwindigkeit-Zeit-Geraden kann größer, gleich oder kleiner Null sein.
Die Steigung einer 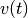 -Geraden hat folgende Bedeutung:
-Geraden hat folgende Bedeutung:
- Umso steiler die Geschwindigkeit-Zeit-Gerade ist, desto größer ist die Beschleunigung.
- Ist die Beschleunigung des beobachteten Objekts gleich Null, so entspricht die
Geschwindigkeit-Zeit-Linie einer waagrechten Geraden. Dies gilt gleichermaßen
für ruhende und sich mit konstanter Geschwindigkeit
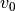 bewegende Objekte.
bewegende Objekte. - Eine Beschleunigung entgegen der ursprünglich als „positiv“ festgelegten
Raumrichtung erhält ein negatives Vorzeichen – egal, ob das beobachtete
Objekt ruht oder sich mit einer konstanten Geschwindigkeit
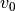 fortbewegt. Dies hat – je nach Wert der Anfangsgeschwindigkeit
fortbewegt. Dies hat – je nach Wert der Anfangsgeschwindigkeit 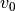 –
eine Beschleunigung „in Gegenrichtung“ beziehungsweise ein kontinuierliches
Abbremsen zur Folge.
–
eine Beschleunigung „in Gegenrichtung“ beziehungsweise ein kontinuierliches
Abbremsen zur Folge.
Aus einem 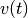 -Diagramm kann also die Beschleunigung zu einem Zeitpunkt
-Diagramm kann also die Beschleunigung zu einem Zeitpunkt
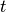 ermittelt werden, indem man an dieser Stelle nicht den Wert, sondern
die Steigung der Diagramm-Linie betrachtet. Beispielsweise gilt für einen
Bremsvorgang
ermittelt werden, indem man an dieser Stelle nicht den Wert, sondern
die Steigung der Diagramm-Linie betrachtet. Beispielsweise gilt für einen
Bremsvorgang 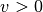 , während für die Geschwindigkeitsänderung (und somit
für die Steigung des Graphen)
, während für die Geschwindigkeitsänderung (und somit
für die Steigung des Graphen) 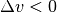 gilt.
gilt.
Beschleunigung und Wegstrecke
Zeichnet man in ein 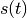 -Diagramm die zurückgelegte Wegstrecke in
Abhängigkeit von der Zeit ein, so hat der Graph bei einer beschleunigten
Bewegung
-Diagramm die zurückgelegte Wegstrecke in
Abhängigkeit von der Zeit ein, so hat der Graph bei einer beschleunigten
Bewegung 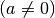 ein parabelförmigen Verlauf. Die konkrete Form der
Parabel hängt von der Anfangsgeschwindigkeit
ein parabelförmigen Verlauf. Die konkrete Form der
Parabel hängt von der Anfangsgeschwindigkeit 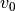 und der anfänglichen Entfernung
und der anfänglichen Entfernung 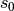 des Objekts vom Beobachter
(Koordinatenursprung) ab.
des Objekts vom Beobachter
(Koordinatenursprung) ab.
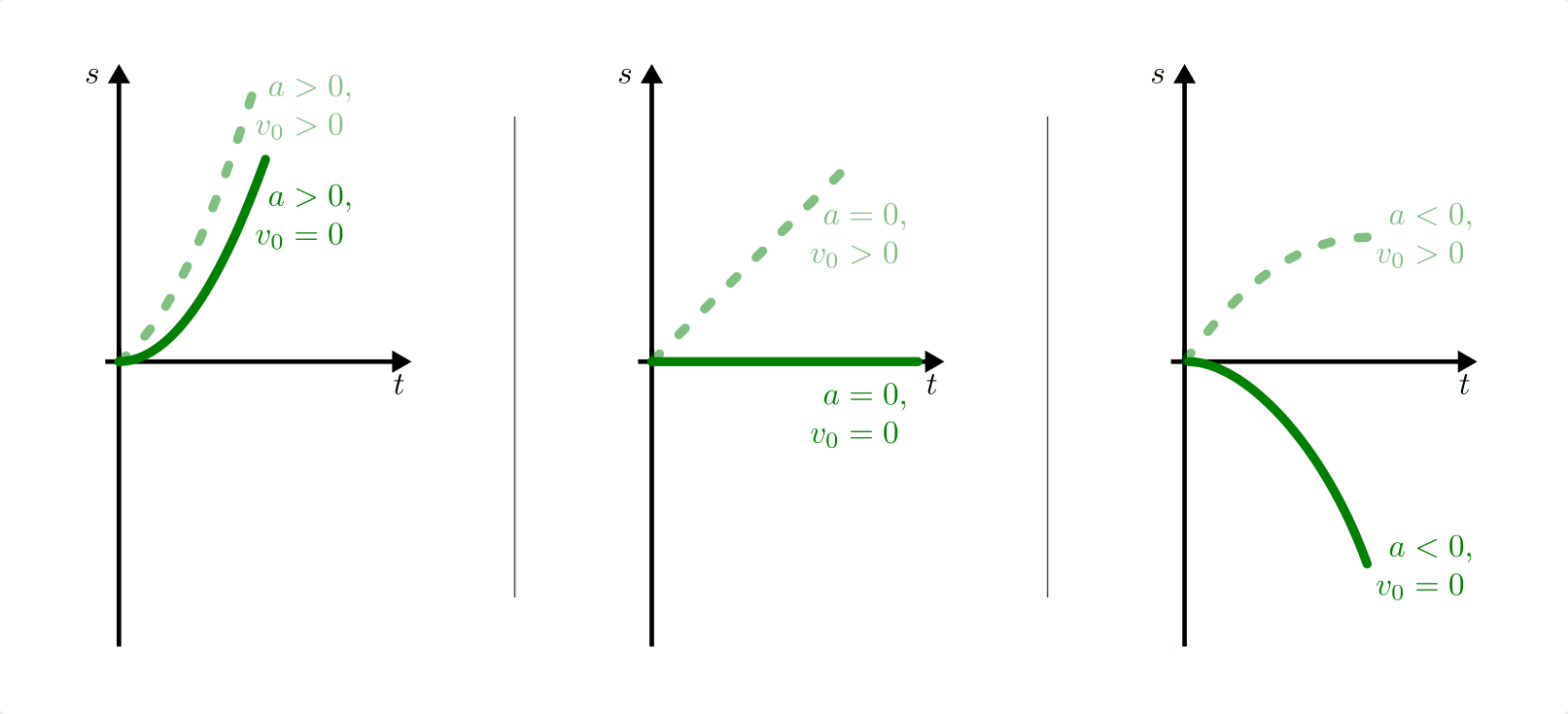
Weg-Zeit-Diagramme einer konstanten Beschleunigung. Für 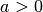 ist
die Weg-Zeit-Parabel nach oben, für
ist
die Weg-Zeit-Parabel nach oben, für 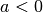 nach unten geöffnet
(linkes bzw. rechtes Bild). Für
nach unten geöffnet
(linkes bzw. rechtes Bild). Für 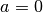 entspricht die
Weg-Zeit-Funktion einer Bewegung mit konstanter Geschwindigkeit (mittleres
Bild).
entspricht die
Weg-Zeit-Funktion einer Bewegung mit konstanter Geschwindigkeit (mittleres
Bild).
Wegstrecken in 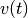 -Diagrammen ablesen
-Diagrammen ablesen
Zunächst soll angenommen werden, dass zum Zeitpunkt 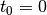 die Bewegung
am Koordinatenursprung
die Bewegung
am Koordinatenursprung 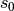 mit einer Startgeschwindigkeit von
mit einer Startgeschwindigkeit von
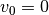 beginnt. In diesem Fall gilt:
beginnt. In diesem Fall gilt:
(2)¶
Diesen Zusammenhang kann man sich anschaulich erklären, indem man bedenkt, dass
sich eine zurückgelegte Wegstrecke letztlich ein Produkt aus Geschwindigkeit und
Zeit darstellt. Stellt man sich den Zeitabschnitt 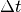 , in dem die
Beschleunigung stattfindet, nochmals in viele kleine Zeitabschnitte
, in dem die
Beschleunigung stattfindet, nochmals in viele kleine Zeitabschnitte
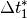 ,
, 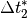 ,
, 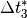 usw.
unterteilt vor (wie bei einer Betrachtung des Vorgangs mit Stroboskop-Licht), so
kann man in diesen kurzen Momenten die jeweiligen Geschwindigkeiten
usw.
unterteilt vor (wie bei einer Betrachtung des Vorgangs mit Stroboskop-Licht), so
kann man in diesen kurzen Momenten die jeweiligen Geschwindigkeiten
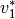 ,
, 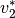 ,
, 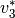 usw. jeweils in guter Näherung
als konstant annehmen.
usw. jeweils in guter Näherung
als konstant annehmen.
Bei einer solchen Aufteilung in viele kleine Zeitschritte mit jeweils konstanten
Geschwindigkeiten lassen sich die in den einzelnen Zeitschritten zurückgelegten
Wegstrecken mittels der Formel 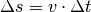 berechnen;
die Einzelergebnisse können dann zum Gesamtergebnis aufsummiert werden. In einem
berechnen;
die Einzelergebnisse können dann zum Gesamtergebnis aufsummiert werden. In einem
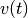 -Diagramm entsprechen die so berechneten einzelnen Wegstrecken den
Rechteck-Flächen zwischen der (stufenförmigen) Geschwindigkeit und der
-Diagramm entsprechen die so berechneten einzelnen Wegstrecken den
Rechteck-Flächen zwischen der (stufenförmigen) Geschwindigkeit und der
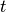 -Achse.
-Achse.
Ist die Beschleunigung konstant, so nimmt die Geschwindigkeit  des sich
bewegenden Objekts linear mit der Zeit zu. Der Mittelwert der einzelnen
Geschwindigkeiten während des Beschleunigungsvorgangs entspricht wiederum der
Durchschnittsgeschwindigkeit
des sich
bewegenden Objekts linear mit der Zeit zu. Der Mittelwert der einzelnen
Geschwindigkeiten während des Beschleunigungsvorgangs entspricht wiederum der
Durchschnittsgeschwindigkeit 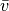 des Objekts:
des Objekts:
(3)¶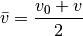
Mit 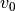 wird hierbei wiederum die Geschwindigkeit zu Beginn der
Beschleunigung, mit
wird hierbei wiederum die Geschwindigkeit zu Beginn der
Beschleunigung, mit  die (End-)Geschwindigkeit zum Zeitpunkt
die (End-)Geschwindigkeit zum Zeitpunkt 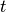 bezeichnet. Ist insbesondere die Startgeschwindigkeit
bezeichnet. Ist insbesondere die Startgeschwindigkeit 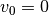 , so ist
, so ist
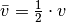 , also gleich der Hälfte der
Endgeschwindigkeit. In diesem Fall gilt somit für die während des
Beschleunigungsvorgangs zurückgelegte Wegstrecke:
, also gleich der Hälfte der
Endgeschwindigkeit. In diesem Fall gilt somit für die während des
Beschleunigungsvorgangs zurückgelegte Wegstrecke:
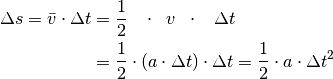
Der Hintergedanke bei dieser Gleichung ist, dass während des
Beschleunigungsvorgangs – über alle kleinen Zeitschritte gemittelt – die
durchschnittliche „Höhe“ der Rechtecke gleich der Durchschnittsgeschwindigkeit
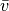 ist; die Gesamt-Fläche zwischen der
ist; die Gesamt-Fläche zwischen der 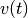 -Linie und der
-Linie und der
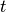 -Achse ist also identisch mit der Fläche, die man erhält, wenn man die
Durchschnittsgeschwindigkeit
-Achse ist also identisch mit der Fläche, die man erhält, wenn man die
Durchschnittsgeschwindigkeit 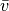 mit
mit 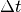 multipliziert.[1]
multipliziert.[1]
Die gleiche Überlegung trifft ebenso zu, wenn die Anfangsgeschwindigkeit
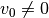 ist. In diesem Fall gilt für die Durchschnittsgeschwindigkeit:
ist. In diesem Fall gilt für die Durchschnittsgeschwindigkeit:
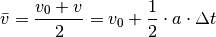
Die Durchschnittsgeschwindigkeit ist also allgemein gleich dem Mittelwert
zwischen der Start- und Endgeschwindigkeit; bei einer konstanten Beschleunigung
 wird sie zur Hälfte der Beschleunigungszeit
wird sie zur Hälfte der Beschleunigungszeit 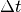 , also zum
Zeitpunkt
, also zum
Zeitpunkt 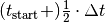 erreicht.
Setzt man wiederum diesen Term für
erreicht.
Setzt man wiederum diesen Term für 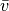 in die Bewegungsgleichung
ein, so erhält man:
in die Bewegungsgleichung
ein, so erhält man:
(4)¶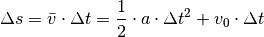
Diese Gleichung gibt allgemein den Zusammenhang zwischen der zurückgelegten
Wegstrecke 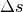 , der Beschleunigung
, der Beschleunigung  , der
Anfangsgeschwindigkeit
, der
Anfangsgeschwindigkeit 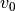 und der Zeitdauer
und der Zeitdauer 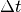 an.
an.
Die allgemeine Bewegungsgleichung
Die Gleichung (4) ist tatsächlich eine Verallgemeinerung der bislang betrachteten Fälle:
Ist die Beschleunigung
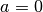 , so erhält man die Ortsgleichung für
Bewegungen mit konstanter Geschwindigkeit:
, so erhält man die Ortsgleichung für
Bewegungen mit konstanter Geschwindigkeit: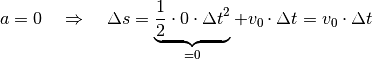
Ist die Anfangsgeschwindigkeit
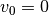 , so erhält man die
Ortsgleichung (2) für Bewegungen
mit konstanter Beschleunigung ohne Anfangsgeschwindigkeit:
, so erhält man die
Ortsgleichung (2) für Bewegungen
mit konstanter Beschleunigung ohne Anfangsgeschwindigkeit: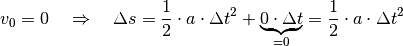
Man kann sich eine beschleunigte Bewegung mit Anfangsgeschwindigkeit also als zwei Prozesse vorstellen, die gleichzeitig ablaufen, ohne sich gegenseitig zu beeinflussen (einmal die Bewegung mit der konstanten Anfangsgeschwindigkeit und einmal die Bewegung mit der konstanten Beschleunigung ohne Anfangsgeschwindigkeit). Beide Teilprozesse können somit getrennt voneinander betrachtet und ihre Effekte addiert werden.
Den konkreten Ort 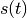 eines Objekts erhält man schließlich, indem man
bei der Bewegung dessen anfängliche Entfernung vom Koordinatenursprung
eines Objekts erhält man schließlich, indem man
bei der Bewegung dessen anfängliche Entfernung vom Koordinatenursprung
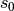 mit berücksichtigt:
mit berücksichtigt:
(5)¶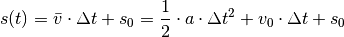
Diese Formel genügt in Kombination mit der Formel 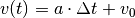 bereits, um den Ort sowie die Geschwindigkeit eines Objekts zu jedem
beliebigen Zeitpunkt angeben zu können, sofern die Startwerte bekannt sind und
die Beschleunigung konstant ist.[2]
bereits, um den Ort sowie die Geschwindigkeit eines Objekts zu jedem
beliebigen Zeitpunkt angeben zu können, sofern die Startwerte bekannt sind und
die Beschleunigung konstant ist.[2]
Die Bremsformel¶
Insbesondere für Bremsvorgänge gibt es eine weitere nützliche Formel, die sich
aus der obigen Gleichung (4)
herleiten lässt.[3] Mit einer Anfangsgeschwindigkeit 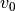 gilt für den
Zusammenhang zwischen
gilt für den
Zusammenhang zwischen  ,
,  und
und 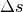 :
:
(6)¶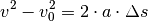
Diese Gleichung wird häufig „Bremsformel“ genannt; im Fall 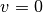 lässt
sich damit der Bremsweg
lässt
sich damit der Bremsweg 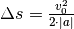 bei
bekannter Anfangsgeschwindigkeit und Beschleunigung unmittelbar berechnen.
Die „Bremsformel“ lässt sich allerdings auch allgemein auf Bewegungen mit
konstanter Beschleunigung anwenden und erleichtert insbesondere dann das
Rechnen, wenn in der Aufgabenstellung keine Zeitangabe enthalten ist.
bei
bekannter Anfangsgeschwindigkeit und Beschleunigung unmittelbar berechnen.
Die „Bremsformel“ lässt sich allerdings auch allgemein auf Bewegungen mit
konstanter Beschleunigung anwenden und erleichtert insbesondere dann das
Rechnen, wenn in der Aufgabenstellung keine Zeitangabe enthalten ist.
Reaktionszeit und Anhalteweg
Um die gesamte Strecke zu berechnen, die ein Fahrzeug zum Anhalten benötigt, muss neben dem Bremsweg auch die Wegstrecke berücksichtigt werden, die der Fahrer während der Reaktionszeit zurücklegt. Es gilt also:
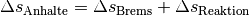
Während der Reaktionszeit, die oftmals vereinfacht als „Schrecksekunde“
angenommen wird, bewegt sich das Fahrzeug mit der konstanten Geschwindigkeit
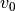 weiter. Es ergibt sich somit mit
weiter. Es ergibt sich somit mit ![t_{\mathrm{Reaktion}}
\stackrel{\wedge}= \unit[1]{s}](../../_images/math/a43b29d14b1a6897c3aba2c15097ff8043e610c0.png) :
:
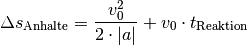
Der Bremsweg (und somit auch der Anhalteweg) nimmt bei der gleichen Bremsbeschleunigung quadratisch mit der Geschwindigkeit zu; aus diesem Grund sind in Ortschaften sowie an unübersichtlichen Stellen Geschwindigkeitsbegrenzungen für die Verkehrssicherheit wichtig.
Beschleunigungen und Kräfte
Beschleunigungen treten allgemein dann auf, wenn eine resultierende Kraft 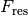 auf einen Gegenstand einwirkt;
für die Beschleunigung gilt dabei
auf einen Gegenstand einwirkt;
für die Beschleunigung gilt dabei 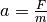 , wobei
, wobei 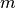 für
die Masse des Gegenstands steht. Kennt man also die auf einen Gegenstand
einwirkenden Kräfte, so kann mittels der obigen Formeln auch dessen Bewegung
vorhergesagt werden; umgekehrt können aus berechneten oder gemessenen
Beschleunigungswerten auch die entsprechenden Kräfte abgeschätzt werden.
für
die Masse des Gegenstands steht. Kennt man also die auf einen Gegenstand
einwirkenden Kräfte, so kann mittels der obigen Formeln auch dessen Bewegung
vorhergesagt werden; umgekehrt können aus berechneten oder gemessenen
Beschleunigungswerten auch die entsprechenden Kräfte abgeschätzt werden.
Anmerkungen:
| [1] | Eine andere, gleichwertige Überlegung ist, dass die Fläche zwischen der
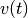 -Linie und der -Linie und der 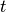 -Achse ein Dreieck darstellt. Dieses
Dreieck entspricht genau der Hälfte des Rechtecks, das man erhält, wenn man -Achse ein Dreieck darstellt. Dieses
Dreieck entspricht genau der Hälfte des Rechtecks, das man erhält, wenn man
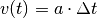 mit mit 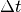 multipliziert. In
beiden Fällen sind die berechneten Flächen identisch. multipliziert. In
beiden Fällen sind die berechneten Flächen identisch. |
| [2] | Bei nicht konstanten Beschleunigungen müsste der Prozess in Teilabschnitte mit jeweils konstanten (Durchschnitts-)Beschleunigungen zerlegt werden. Die ist meist mit erheblich mehr Rechenaufwand verbunden und wird kaum ohne Hilfe von Computern berechnet. |
| [3] | Die Bremsformel (6) lässt sich durch folgende Umformungen auf die ursprünglichen Gleichungen (1) und (2) zurückführen:
|
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.