Bernoulli-Experimente¶
Als „Bernoulli-Experiment (benannt nach Jakob Bernoulli) bezeichnet man ein
Zufallsexperiment mit nur zwei möglichen Ergebnissen. Meist verwendet man dabei
als Ergebnismenge  , wobei
, wobei
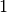 als Symbol für das Eintreten des Ereignisses („Treffer“) und
als Symbol für das Eintreten des Ereignisses („Treffer“) und 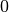 als Symbol für das Nichteintreten des Ereignisses („Niete“) benutzt wird.
Zusätzlich ist es üblich, mit
als Symbol für das Nichteintreten des Ereignisses („Niete“) benutzt wird.
Zusätzlich ist es üblich, mit 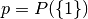 die Wahrscheinlichkeit für
einen Treffer und mit
die Wahrscheinlichkeit für
einen Treffer und mit 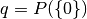 die Wahrscheinlichkeit für eine
Niete zu bezeichnen.
die Wahrscheinlichkeit für eine
Niete zu bezeichnen.
Wird ein Bernoulli-Experiment mehrfach durchgeführt, wobei sich die einzelnen Versuchen nicht beeinflussen und die Trefferwahrscheinlichkeiten bei allen Versuchen gleich groß sind, so spricht man von einer Bernoulli-Kette. Eine solche Bernoulli-Kette lässt sich ebenfalls durch einen Ergebnisbaum veranschaulichen.
Betrachtet man ein Ereignis mit genau 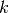 Treffern, so lassen sich mittels
des Ergebnisbaums folgende Gesetzmäßigkeiten herleiten:
Treffern, so lassen sich mittels
des Ergebnisbaums folgende Gesetzmäßigkeiten herleiten:
- Jeder einzelne Weg im Ereignisbaum, der über
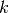 Einsen und
Einsen und  Nullen führt, setzt sich aus
Nullen führt, setzt sich aus 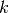 Teilstücken mit der Wahrscheinlichkeit
Teilstücken mit der Wahrscheinlichkeit
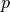 sowie
sowie  Teilstücken mit der Wahrscheinlichkeit
Teilstücken mit der Wahrscheinlichkeit
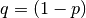 zusammen.
Nach der Multiplikationsregel für bedingte Wahrscheinlichkeiten ist somit die
Wahrscheinlichkeit für jeden Weg mit genau
zusammen.
Nach der Multiplikationsregel für bedingte Wahrscheinlichkeiten ist somit die
Wahrscheinlichkeit für jeden Weg mit genau 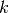 Treffern gleich
Treffern gleich
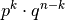 .
. - Um die Anzahl an Wegen mit genau
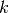 Einsen zu ermitteln, muss bestimmt
werden, auf wie viele verschiedene Arten es möglich ist,
Einsen zu ermitteln, muss bestimmt
werden, auf wie viele verschiedene Arten es möglich ist, 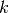 Einsen auf
Einsen auf
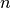 Stellen zu verteilen. Es handelt sich hierbei um Kombinationen ohne
Wiederholung, da jeder Weg nur einmal gezählt werden darf und die Reihenfolge,
in der die einzelnen Wege gezählt werden, ohne Bedeutung ist. Dies entspricht
dem klassischen „Lotto-Problem“, d.h. es gibt
Stellen zu verteilen. Es handelt sich hierbei um Kombinationen ohne
Wiederholung, da jeder Weg nur einmal gezählt werden darf und die Reihenfolge,
in der die einzelnen Wege gezählt werden, ohne Bedeutung ist. Dies entspricht
dem klassischen „Lotto-Problem“, d.h. es gibt 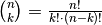 verschiedene Kombinationen.
verschiedene Kombinationen.
Aus beiden Eigenschaften ergibt sich folgende Wahrscheinlichkeit, dass bei einer
Bernoulli-Kette mit einer Länge 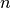 und einer Wahrscheinlichkeit
und einer Wahrscheinlichkeit
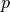 genau
genau 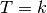 Treffer auftreten:
Treffer auftreten:
(1)¶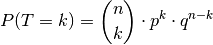
Diese Formel wird häufig als „Formel von Bernoulli“ bezeichnet.
Summenwahrscheinlichkeiten bei Bernoulli-Ketten
Bezeichnet man bei einer Bernoulli-Kette mit einer Länge 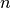 und einer
Trefferwahrscheinlichkeit
und einer
Trefferwahrscheinlichkeit 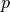 das Ereignis „genau
das Ereignis „genau 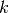 Treffer“ mit
Treffer“ mit
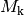 , so gilt:
, so gilt:
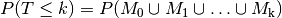
und
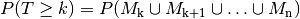
Alle Ereignisse 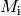 , die jeweils
, die jeweils 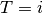 Treffer bedeuten,
sind paarweise stochastisch unabhängig; die einzelnen Wahrscheinlichkeiten
können also addiert werden.
Treffer bedeuten,
sind paarweise stochastisch unabhängig; die einzelnen Wahrscheinlichkeiten
können also addiert werden.
Für ein Bernoulli-Experiment mit einer Länge 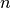 und einer
Trefferwahrscheinlichkeit
und einer
Trefferwahrscheinlichkeit 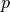 gelten somit folgende Regeln:
gelten somit folgende Regeln:
Für mindestens
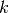 Treffer:
Treffer: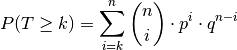
Für höchstens
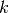 Treffer:
Treffer: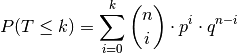
Für mindestens
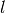 und höchstens
und höchstens 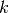 Treffer:
Treffer: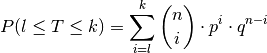
… to be continued …
