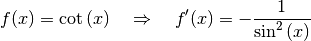Ableitungen von trigonometrischen Funktionen¶
Im Folgenden sollen die Ableitungen der trigonometrischen Funktionen 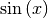 ,
, 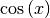 ,
,
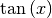 und
und 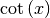 hergeleitet werden.
hergeleitet werden.
Ableitung der Sinusfunktion
Um eine Ableitungsregel für die Sinusfunktion 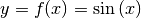 herzuleiten, geht man vom Differentialquotienten
herzuleiten, geht man vom Differentialquotienten 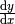 aus. Dieser lautet
für die Sinusfunktion:
aus. Dieser lautet
für die Sinusfunktion:
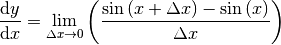
Mittels des Additionstheorems 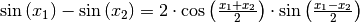 kann der Zählerterm folgendermaßen
umgeschrieben werden:
kann der Zählerterm folgendermaßen
umgeschrieben werden:
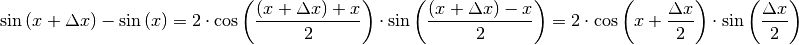
Damit kann der Differentialquotient in folgender Form geschrieben werden:
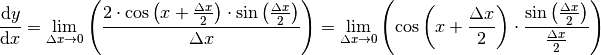
Im letzten Rechenschritt wurde der Faktor 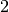 in Form eines Doppelbruchs
in den Nenner gezogen, um die Form auf der rechten Seite zu erhalten. Der
Differentialquotient ist als Grenzwert eines Produkts zweier Funktionen gemäß
den Rechenregeln für Grenzwerte gleich dem
Produkt der Grenzwerte beider Funktionen. Für den Grenzwert des ersten Faktors
gilt:
in Form eines Doppelbruchs
in den Nenner gezogen, um die Form auf der rechten Seite zu erhalten. Der
Differentialquotient ist als Grenzwert eines Produkts zweier Funktionen gemäß
den Rechenregeln für Grenzwerte gleich dem
Produkt der Grenzwerte beider Funktionen. Für den Grenzwert des ersten Faktors
gilt:
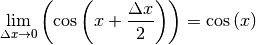
Der Grenzwert des zweiten Faktors kann zur besseren Lesbarkeit als 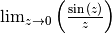 mit
mit 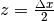 geschrieben werden. Um diesen Grenzwert für kleine Werte von
geschrieben werden. Um diesen Grenzwert für kleine Werte von  abzuschätzen, kann man die Sinusfunktion mit der Cosinus- und der
Tangensfunktion vergleichen. Dabei gilt mit
abzuschätzen, kann man die Sinusfunktion mit der Cosinus- und der
Tangensfunktion vergleichen. Dabei gilt mit 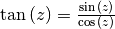 :
:
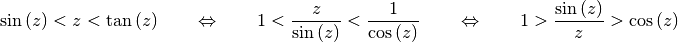
Im ersten Rechenschritt wurde durch 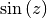 dividiert, im zweiten
wurden die Kehrwerte der Terme betrachtet, wobei sich die Ungleichheitszeichen
umkehren. Wegen
dividiert, im zweiten
wurden die Kehrwerte der Terme betrachtet, wobei sich die Ungleichheitszeichen
umkehren. Wegen 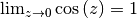 wird die Ungleichung zu
wird die Ungleichung zu
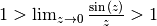 , also muss gelten:
, also muss gelten:
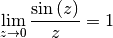
Für die Ableitung der Sinus-Funktion folgt damit:
(1)¶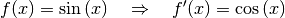
Die Ableitung der Sinus-Funktion ist also gleich der Cosinus-Funktion.
Ableitung der Cosinusfunktion
Die Ableitung der Cosinus-Funktion kann mit Hilfe der Ableitungsregel der
Sinusfunktion anhand des Zusammenhangs 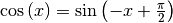 bestimmt werden; dabei wird wiederum die
Kettenregel verwendet. Mit
bestimmt werden; dabei wird wiederum die
Kettenregel verwendet. Mit 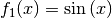 als
der äußeren und
als
der äußeren und 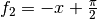 als der inneren Funktion gilt:
als der inneren Funktion gilt:
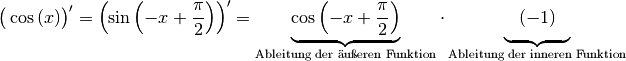
Da 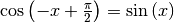 gilt, folgt für
die Ableitung der Cosinus-Funktion:
gilt, folgt für
die Ableitung der Cosinus-Funktion:
(2)¶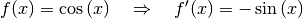
Die Ableitung der Cosinus-Funktion ist also gleich der negativen Sinusfunktion.
Ableitung der Tangens- und Cotangensfunktion
Die Ableitung der Tangensfunktion 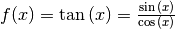 kann mit Hilfe der Ableitungsregeln der Sinus- und
Cosinusfunktion bestimmt werden; dabei wird wiederum die Quotientenregel verwendet:
kann mit Hilfe der Ableitungsregeln der Sinus- und
Cosinusfunktion bestimmt werden; dabei wird wiederum die Quotientenregel verwendet:
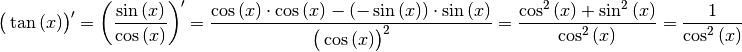
Für die Ableitung der Tangensfunktion gilt also:
(3)¶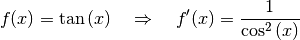
Für die Cotangensfunktion 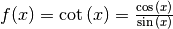 gilt entsprechend:
gilt entsprechend:
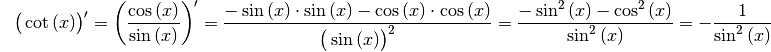
Für die Ableitung der Cotangensfunktion gilt also:
(4)¶