Strecken und Geraden¶
Jeder Punkt 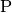 eines kartesischen Koordinatensystems kann
mittels seines Ortsvektors, also mittels seiner
eines kartesischen Koordinatensystems kann
mittels seines Ortsvektors, also mittels seiner 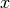 -,
-,
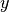 - und
- und  -Koordinaten eindeutig dargestellt werden.
-Koordinaten eindeutig dargestellt werden.
Betrachet man mehrere Punkte mit unterschiedlichen Ortsvektoren, so lassen sich auch die Strecken zwischen den einzelnen Punkten mittels (normaler) Vektoren darstellen. Die Vektorrechung kann somit unmittelbar auf die Beschreibung von Strecken und Geraden angewendet werden.
Strecken und Teilverhältnisse¶
Bezeichnet man die zu zwei Punkten 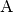 und
und 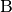 gehörenden Ortsvektoren mit
gehörenden Ortsvektoren mit 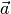 und
und 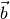 , so ist die
Verbindung zwischen diesen beiden Punkten durch den so genannten
„Verschiebungsvektor“
, so ist die
Verbindung zwischen diesen beiden Punkten durch den so genannten
„Verschiebungsvektor“ 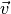 charakterisiert:
charakterisiert:
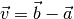
Die einzelnen Koordinaten des Verbindungsvektors erhält man, indem man die Koordinaten des Ausgangspunkts von den Koordinaten des Endpunkts subtrahiert:
(1)¶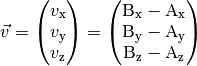
Im zweidimensionalen Fall entfällt die dritte Koordinate.
Mittels des Verschiebungsvektors 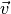 gelangt man vom Punkt
gelangt man vom Punkt
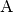 zum Punkt
zum Punkt 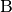 , indem man diesen zum
Ortsvektor des Punktes
, indem man diesen zum
Ortsvektor des Punktes 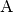 addiert:
addiert:
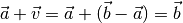
Eine Strecke lässt sich somit wahlweise durch die Angabe zweier Punkte
(beziehungsweise deren Ortsvektoren) oder auch durch Angabe eines Ortsvektors
sowie des Verschiebungsvektors 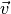 beider Punkte beschreiben:
beider Punkte beschreiben:
(2)¶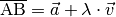
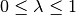 ist notwendig, da eine Strecke die Menge
aller Punkte zwischen den zwei Endpunkten darstellt; dies ist äquivalent dazu,
dass man zum Ausgangspunkt einen beliebigen Bruchteil (kleiner oder gleich
ist notwendig, da eine Strecke die Menge
aller Punkte zwischen den zwei Endpunkten darstellt; dies ist äquivalent dazu,
dass man zum Ausgangspunkt einen beliebigen Bruchteil (kleiner oder gleich
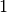 ) des Verschiebungsvektors hinzu addiert.
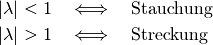
) des Verschiebungsvektors hinzu addiert.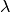 selbst wird „Linearfaktor“ genannt: Er gibt als reiner Zahlenwert („Skalar“)
an, um welchen Faktor der mit ihm multiplizierte Vektor skaliert, also
gestaucht beziehungsweise gestreckt wird. Ist der Wert von
selbst wird „Linearfaktor“ genannt: Er gibt als reiner Zahlenwert („Skalar“)
an, um welchen Faktor der mit ihm multiplizierte Vektor skaliert, also
gestaucht beziehungsweise gestreckt wird. Ist der Wert von 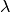 negativ, so wird die Richtung des mit ihm multiplizierten Vektors umgekehrt.
negativ, so wird die Richtung des mit ihm multiplizierten Vektors umgekehrt.Beispiel:
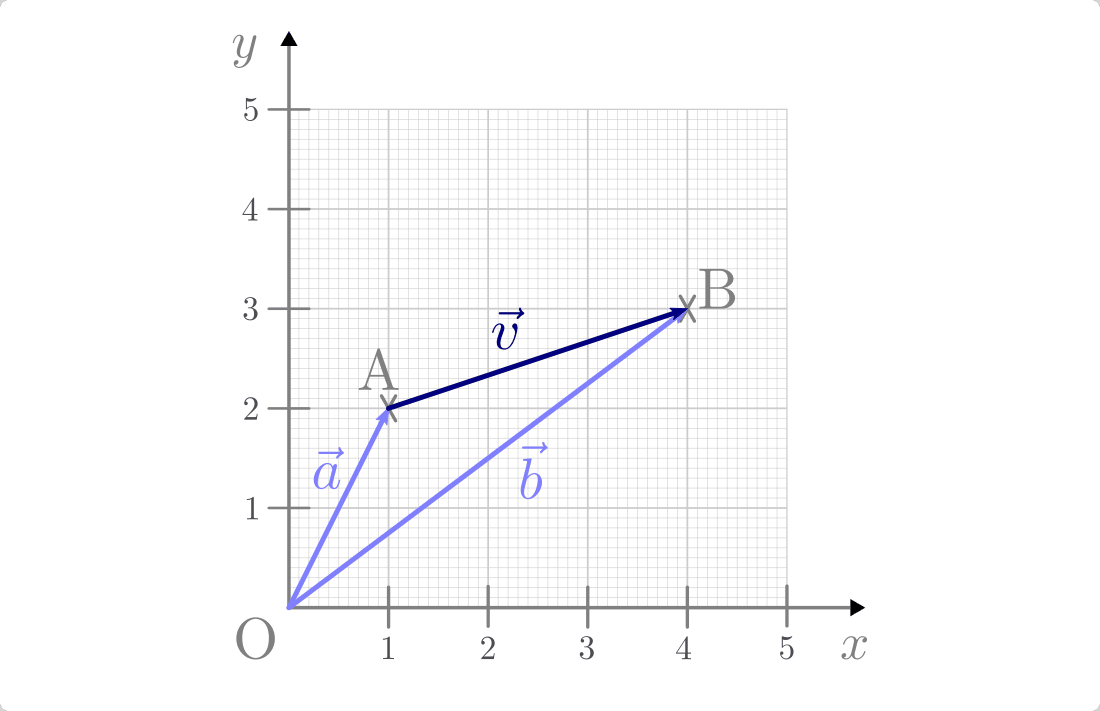
In der obigen Abbildung hat der Punkt
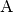 die Koordinaten
die Koordinaten
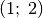 und der Punkt
und der Punkt 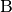 die Koordinaten
die Koordinaten
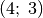 . Wie lässt sich die Strecke
. Wie lässt sich die Strecke 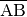 mittels zweier Vektoren darstellen?
mittels zweier Vektoren darstellen?Der Verschiebungsvektor
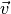 zwischen
zwischen 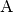 und
und
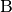 ergibt sich aus der Differenz der beiden Ortsvektoren:
ergibt sich aus der Differenz der beiden Ortsvektoren: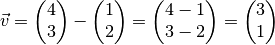
Mit dem Punkt
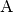 als Ausgangspunkt erhält man damit folgende
Darstellung der Verbindungslinie zwischen
als Ausgangspunkt erhält man damit folgende
Darstellung der Verbindungslinie zwischen 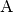 und
und  :
: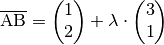
Auch hier muss wiederum
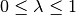 gelten.
gelten.
Das Teilverhältnis¶
Für die folgenden Überlegungen wird wiederum eine Strecke
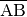 betrachtet, die durch einen Punkt auf ihr
liegenden Punkt
betrachtet, die durch einen Punkt auf ihr
liegenden Punkt 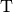 in zwei Abschnitte unterteilt wird.
in zwei Abschnitte unterteilt wird.
Das so genannte „Teilverhältnis“ 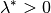 gibt dabei an, in
welchem Verhältnis
gibt dabei an, in
welchem Verhältnis 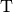 die Strecke
die Strecke 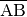 teilt:
teilt:
(3)¶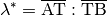
Der Wertebereich von 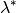 liegt zwischen Null und Unendlich:
liegt zwischen Null und Unendlich:
- Ist der Teilpunkt
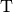 identisch mit dem Punkt
identisch mit dem Punkt
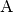 , so ist
, so ist 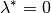 .
. - Halbiert der Teilpunkt
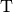 die Strecke
die Strecke
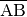 , so ist
, so ist 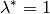 .
. - Nähert sich der Teilpunkt
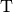 zunehmend dem Punkt
zunehmend dem Punkt
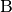 , so geht der Wert des Teilverhältnisses
, so geht der Wert des Teilverhältnisses 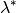 gegen Unendlich. Für
gegen Unendlich. Für 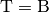 ist das
Teilverhältnis nicht definiert.
ist das
Teilverhältnis nicht definiert.
Kennt man die Koordinaten der Punkte 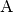 und
und 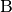 sowie das Teilverhältnisses
sowie das Teilverhältnisses 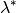 so ergeben sich folgende
Streckenlängen für
so ergeben sich folgende
Streckenlängen für  beziehungsweise
beziehungsweise
 :
:
(4)¶![\overline{\mathrm{AT}} &= \left|\frac{\lambda^{*}}{\lambda^{*}+1}\right|
\cdot \overline{\mathrm{AB}} \\[6pt]
\overline{\mathrm{TB}} &= \left|\frac{1}{\lambda^{*}+1}\right| \cdot
\overline{\mathrm{AB}}](../_images/math/a1e6960f49070881fe031c417e26bfc79808f2d1.png)
Beispiel:
Eine Strecke hat die Endpunkte
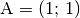 und
und
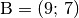 . Wie weit ist der Punkt
. Wie weit ist der Punkt 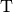 , der
die Strecke
, der
die Strecke 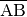 im Verhältnis
im Verhältnis 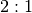 teilt,
von
teilt,
von 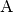 entfernt?
entfernt?Um zu bestimmen, wie weit der Punkt
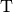 von
von 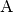 entfernt ist, muss die Länge der Strecke
entfernt ist, muss die Länge der Strecke  bestimmt werden. Dies ist mittels der obigen Formel möglich, wenn man zunächst
die Länge der Strecke
bestimmt werden. Dies ist mittels der obigen Formel möglich, wenn man zunächst
die Länge der Strecke 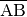 berechnet:
berechnet: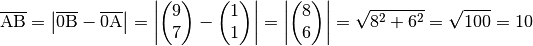
Mit dem Teilungsverhältnis
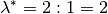 ergibt sich gemäß der
obigen Formel für die Länge der Strecke
ergibt sich gemäß der
obigen Formel für die Länge der Strecke  :
: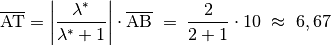
Der Teilpunkt
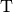 auf der Strecke
auf der Strecke
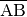 ist somit rund
ist somit rund 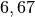 Längeneinheiten vom
Punkt
Längeneinheiten vom
Punkt 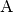 entfernt.
entfernt.
Koordinaten des Teilpunktes
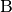 zum Teilpunkt
zum Teilpunkt
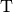 , indem man
, indem man 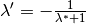 in die
Streckengleichung einsetzt:
in die
Streckengleichung einsetzt:Für den Zum Teilpunkt 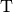 gehörenden Ortsvektor
gehörenden Ortsvektor
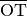 gilt somit:
gilt somit:
![\overrightarrow{\mathrm{OT}} = \vec{a} + \left(
\frac{\lambda^{*}}{\lambda^{*} + 1} \right) \cdot \vec{v} \\[4pt]
\overrightarrow{\mathrm{OT}} = \vec{b} - \left( \frac{1}{\lambda^{*} - 1}
\right) \cdot \vec{v}](../_images/math/c7377107b3191582e72c292b3275ad4d7a68a6c9.png)
Setzt man in die erste der beiden obigen Gleichungen 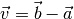 ein, so erhält man:
ein, so erhält man:
![\overrightarrow{\mathrm{OT}} &= \vec{a} + \left(
\frac{\lambda^{*}}{\lambda^{*} + 1} \right) \cdot \left( \vec{b} - \vec{a}
\right) \\[4pt]
&= \vec{a} + \left( \frac{\lambda^{*}}{\lambda^{*} +
1} \right) \cdot \vec{b} - \left( \frac{\lambda^{*}}{\lambda^{*} + 1}\right)
\cdot \vec{a}](../_images/math/ae0f1206ac807964b67ea74b32539573aed44564.png)
Um die rechte Seite der Gleichung weiter vereinfachen zu können, kann man
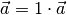 schreiben und
schreiben und 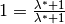 setzen; so erhalten alle Terme den gleichen
(Haupt-)Nenner und können somit zusammengefasst werden:
setzen; so erhalten alle Terme den gleichen
(Haupt-)Nenner und können somit zusammengefasst werden:
![\overrightarrow{\mathrm{OT}} &= \left( \frac{\lambda^{*} + 1}{\lambda^{*} + 1} \right) \cdot \vec{a} +
\left( \frac{\lambda^{*}}{\lambda^{*} + 1} \right) \cdot \vec{b} - \left(
\frac{\lambda^{*}}{\lambda^{*} + 1}\right) \cdot \vec{a} \\[4pt]
&= \left( \frac{1}{\lambda^{*} + 1} \right) \cdot \vec{a} + \left(
\frac{\lambda^{*}}{\lambda^{*} + 1} \right) \cdot \vec{b} \\[4pt]
&= \left( \frac{1}{\lambda^{*} + 1} \right) \cdot \left( \vec{a} +
\lambda^{*} \cdot \vec{b} \right)](../_images/math/0f4c943d8f78fc4aeded8fed29346eef2544ef17.png)
In der zweiten Zeile der obigen Gleichung wurde das Distributivgesetz für
Vektoren genutzt und die hintere Klammer
ausmultipliziert; in der mittleren Zeile wurde dann die Identität 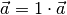 genutzt und
genutzt und 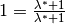 gesetzt, um die additiv beziehungsweise subtraktiv verknüpften Terme auf
einen Hauptnenner bringen zu können.
gesetzt, um die additiv beziehungsweise subtraktiv verknüpften Terme auf
einen Hauptnenner bringen zu können.
Für die Komponenten des Teilpunktes gilt somit:
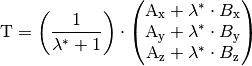
Für den Mittelpunkt 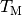 einer Strecke gilt insbesondere
einer Strecke gilt insbesondere
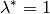 , und somit
, und somit
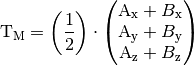
Geraden in einer Ebene¶
Eine Gerade  kann, ebenso wie eine Strecke, mittels eines Punktes
kann, ebenso wie eine Strecke, mittels eines Punktes
 beziehungsweise dessen Ortsvektors
beziehungsweise dessen Ortsvektors  und eines
„Richtungsvektors“
und eines
„Richtungsvektors“ 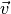 dargestellt werden:
dargestellt werden:
(5)¶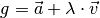
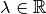 allerdings ein
beliebig großer, gegebenenfalls auch negativer Zahlenwert gewählt werden.
allerdings ein
beliebig großer, gegebenenfalls auch negativer Zahlenwert gewählt werden.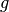 handelt es sich
vielmehr um die Menge aller Punkte, welche die zugehörige Gleichung erfüllen.
handelt es sich
vielmehr um die Menge aller Punkte, welche die zugehörige Gleichung erfüllen.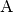 und
und 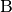 festgelegt werden, so so entspricht der Richtungsvektor
festgelegt werden, so so entspricht der Richtungsvektor 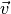 wiederum
dem Verschiebungsvektor (1) beider Punkte.
wiederum
dem Verschiebungsvektor (1) beider Punkte.… to be continued …
Anmerkungen:

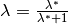 in die Streckengleichung
in die Streckengleichung