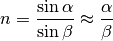Lichtbrechung¶
Trifft Licht auf die Grenzfläche zweier Stoffe, so wird es zum Teil reflektiert, zum Teil verändert es an der Grenze beider Stoffe seine Richtung. Senkrecht auftreffendes Licht ändert seine Richtung nicht.
Das Brechungsgesetz¶
Um das Brechungsgesetz zu formulieren, zeichnet man an der Stelle, an der das
Licht auftrifft, eine Gerade senkrecht zur Grenzfläche. Der Winkel zwischen
dieser Senkrechten und dem einfallenden Strahl wird Einfallswinkel
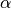 , der Winkel zwischen der Senkrechten und dem gebrochenen Strahl
Brechungswinkel
, der Winkel zwischen der Senkrechten und dem gebrochenen Strahl
Brechungswinkel 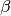 genannt.
genannt.
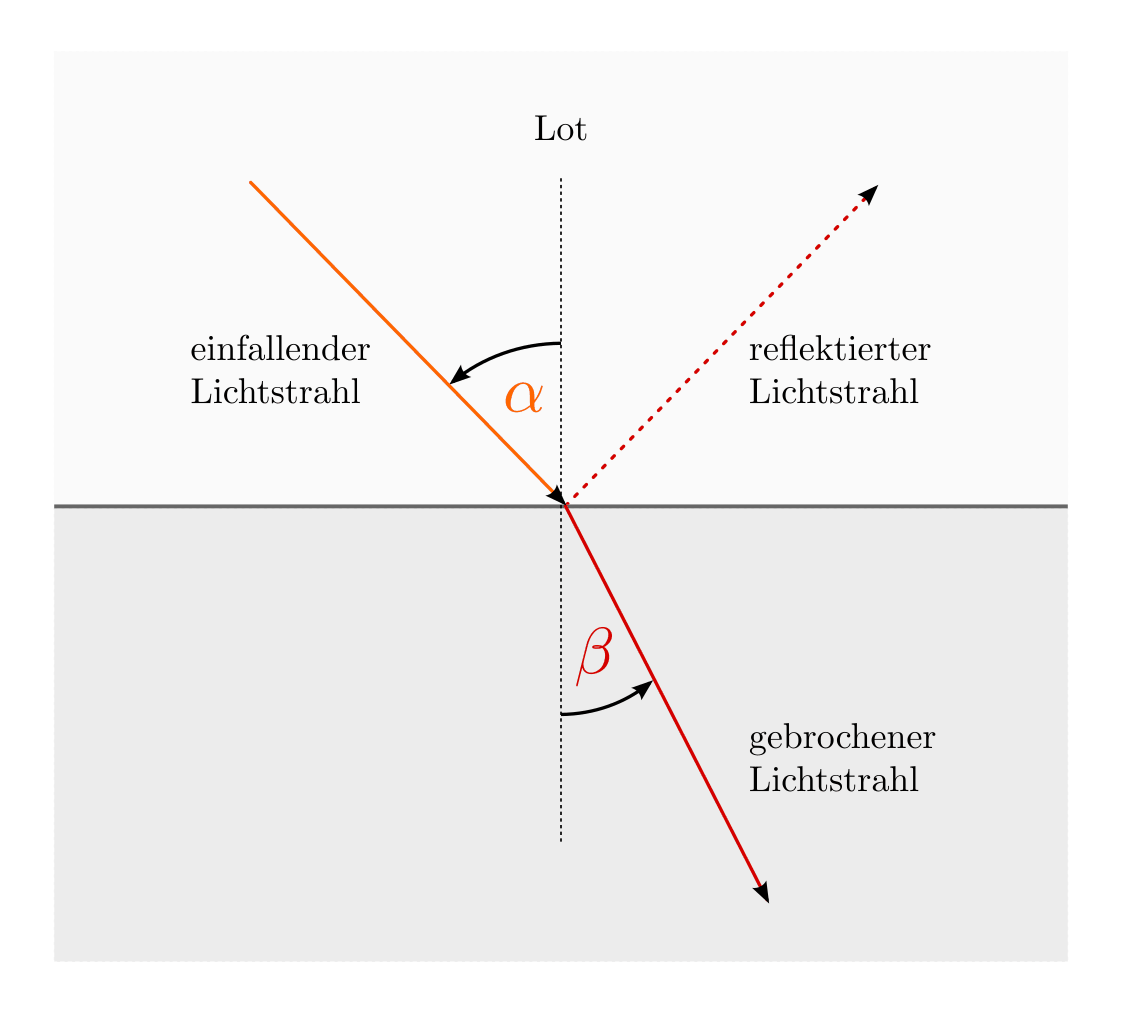
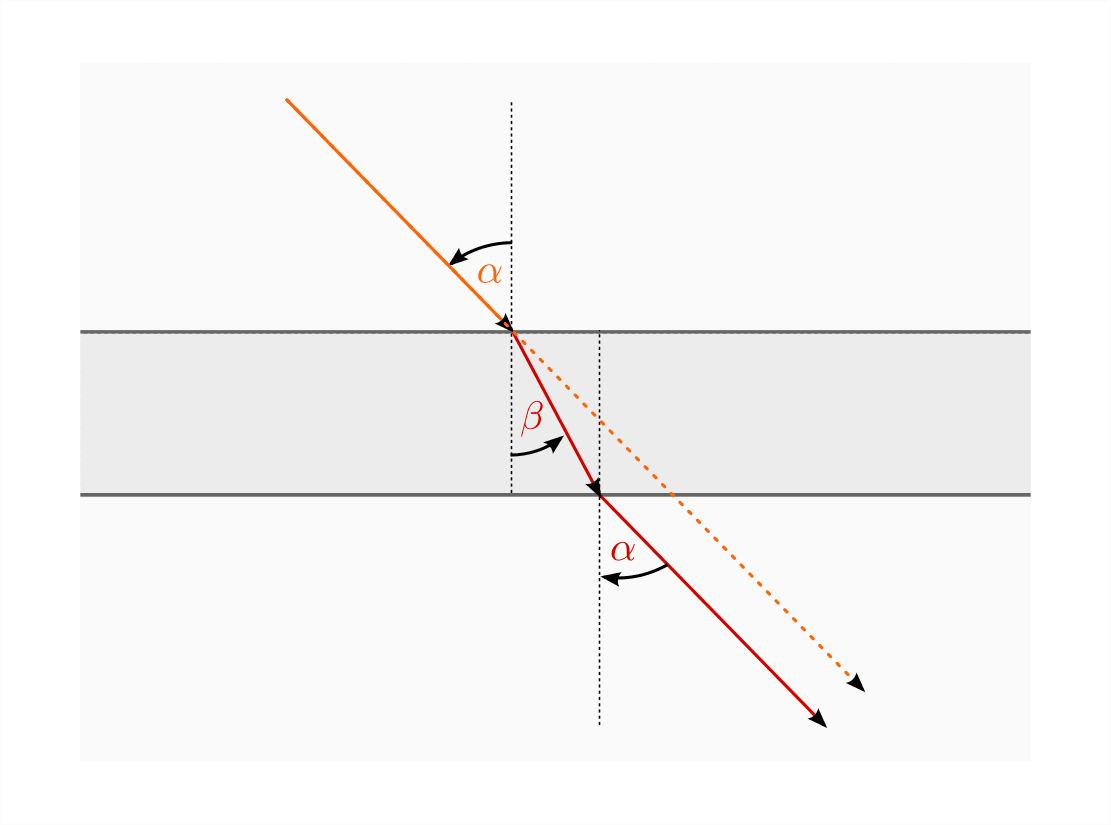
Lichtbrechung beim Übergang eines Lichtstrahls von einem optisch dünnen in ein optisch dickes Medium.
Brechzahl und Brechungsgesetz
Die Sinus-Werte der Einfallswinkel und Brechungswinkel, 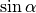 und
und 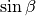 , stehen im gleichen Verhältnis zueinander wie die
Geschwindigkeiten
, stehen im gleichen Verhältnis zueinander wie die
Geschwindigkeiten 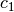 und
und 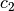 , die das Licht in den jeweiligen
Stoffen erreichen kann. Breitet sich das Licht zunächst in Luft bzw. Vakuum aus
und trifft auf ein transparentes Material, so ergibt das Verhältnis der
Winkelgrößen einen konstanten, vom Material abhängigen Wert, der als
(absolute) Brechzahl
, die das Licht in den jeweiligen
Stoffen erreichen kann. Breitet sich das Licht zunächst in Luft bzw. Vakuum aus
und trifft auf ein transparentes Material, so ergibt das Verhältnis der
Winkelgrößen einen konstanten, vom Material abhängigen Wert, der als
(absolute) Brechzahl 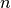 bezeichnet wird:
bezeichnet wird:
(1)¶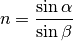
Die (absolute) Brechzahl 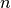 gegenüber dem Vakuum ist eine für jeden Stoff
charakteristische Materialeigenschaft.[1] Sie gibt gleichzeitig das
Verhältnis der Lichtgeschwindigkeit im Vakuum
gegenüber dem Vakuum ist eine für jeden Stoff
charakteristische Materialeigenschaft.[1] Sie gibt gleichzeitig das
Verhältnis der Lichtgeschwindigkeit im Vakuum ![(c_0 = \unit[3,0
\cdot 10^8]{\frac{m}{s}})](../_images/math/d683d0d0c90dec034ddeb54335b5566c35309850.png) zur die Lichtgeschwindigkeit
zur die Lichtgeschwindigkeit  im jeweiligen
Stoff an:
im jeweiligen
Stoff an:
(2)¶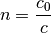
Für die Brechzahl von Vakuum gilt nach der obigen Formel 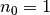 ,
für die Brechzahl von Luft in sehr guter Näherung ebenfalls.[2] In allen
optischen Medien breitet sich das Licht mit geringerer Geschwindigkeit aus, so
dass die (absoluten) Brechzahlen aller Materialien
,
für die Brechzahl von Luft in sehr guter Näherung ebenfalls.[2] In allen
optischen Medien breitet sich das Licht mit geringerer Geschwindigkeit aus, so
dass die (absoluten) Brechzahlen aller Materialien 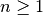 gilt.
gilt.
Die unterschiedlichen Brechzahlen verschiedener Materialien, die in vielen Lehrbüchern und in tabellarischer Form abgedruckt sind, können bei optischen Versuchen zur Materialbestimmung genutzt werden.
| Stoff | Brechzahl 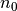 |
| Eis | 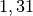 |
| Wasser | 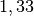 |
| Quarzglas | 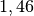 |
| Plexiglas | 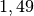 |
| Flintglas | 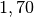 |
| Diamant | 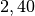 |
Tritt ein Lichtstrahl von einem Stoff mit der Brechzahl 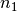 in einen
anderen Stoff mit einer höheren Brechzahl
in einen
anderen Stoff mit einer höheren Brechzahl 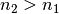 über, so wird er zur
Senkrechten hin gebrochen. In diesem Fall gibt die so genannte relative
Brechzahl
über, so wird er zur
Senkrechten hin gebrochen. In diesem Fall gibt die so genannte relative
Brechzahl 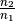 an, in welchem Verhältnis die Sinus-Werte
des Einfalls- und Brechungswinkels stehen:
an, in welchem Verhältnis die Sinus-Werte
des Einfalls- und Brechungswinkels stehen:
(3)¶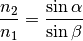
Beispiel:
Licht breitet sich in Glas oder Wasser langsamer aus als in Luft. Das Verhältnis der Lichtgeschwindigkeit in Luft
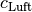 zu der in
Lichtgeschwindigkeit in Wasser
zu der in
Lichtgeschwindigkeit in Wasser 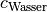 ist daher größer als
ist daher größer als
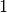 :
:![n_{\mathrm{Luft \rightarrow Wasser}} = \frac{c_{\mathrm{Luft}}}{c_{\mathrm{Wasser}}} =
\frac{\unit[300 000]{\frac{km}{s} } }{\unit[225 000]{\frac{km}{s} } } = 1,33](../_images/math/85875e78c57aa27140001ee30fc64eeefdb538cf.png)
Das bedeutet nichts anderes, als dass der Einfallswinkel
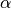 des
Lichts um den Faktor
des
Lichts um den Faktor 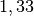 größer ist als der Brechungswinkel
größer ist als der Brechungswinkel
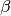 . Das Licht wird zur senkrechten Gerade hin gebrochen.
. Das Licht wird zur senkrechten Gerade hin gebrochen.
Die Totalreflexion
Tritt ein Lichtstrahl von einem optischen Medium mit hoher Brechzahl 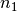 in einen anderen Stoff mit niedriger Brechzahl
in einen anderen Stoff mit niedriger Brechzahl 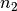 über, so wird
er von der Senkrechten weg gebrochen; der Brechungswinkel
über, so wird
er von der Senkrechten weg gebrochen; der Brechungswinkel 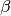 ist in
diesem Fall größer als der Einfallswinkel
ist in
diesem Fall größer als der Einfallswinkel 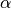 . Konkret gilt:
. Konkret gilt:
(4)¶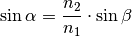
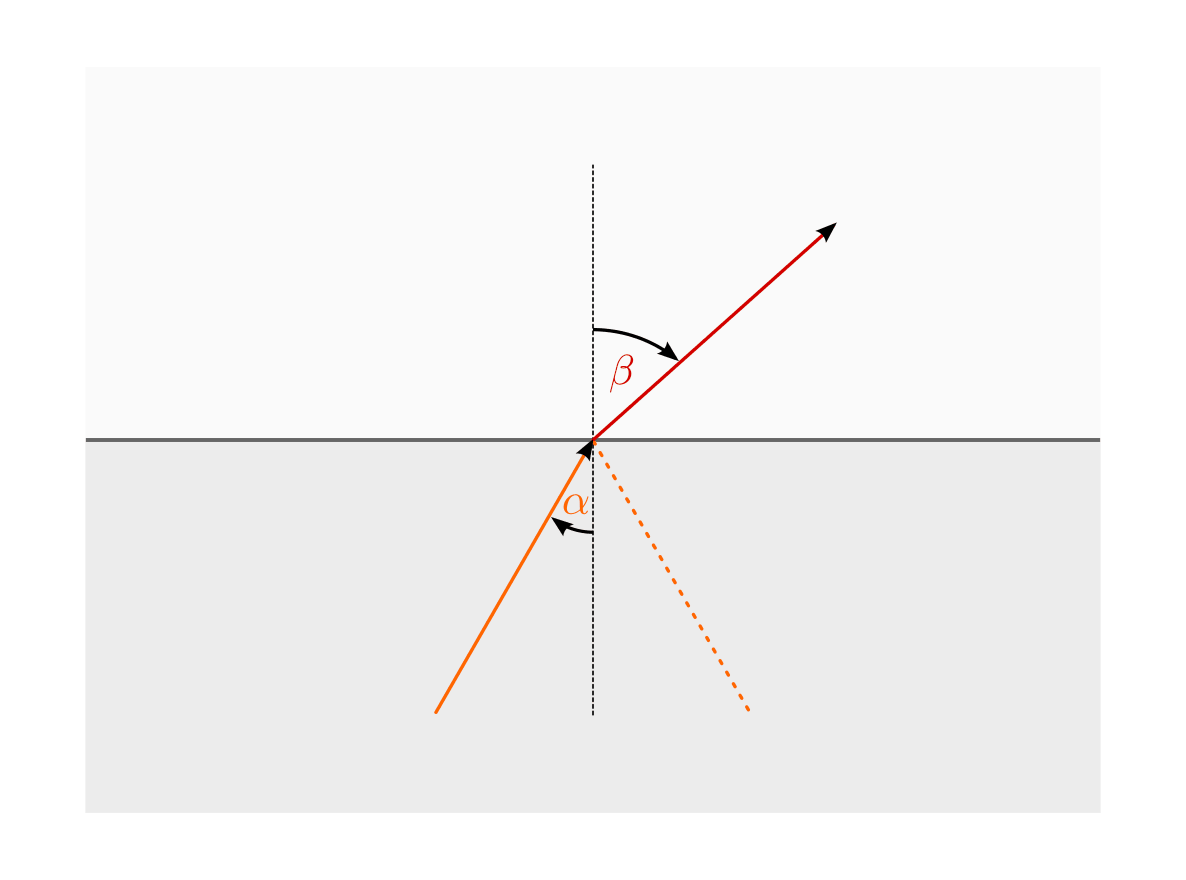
Lichtbrechung beim Übergang eines Lichtstrahls von einem optisch dicken in ein optisch dünnes Medium.
Bei einem bestimmten, von den beiden Materialien abhängigen Einfallswinkel
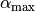 nimmt der Brechungswinkel
nimmt der Brechungswinkel 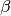 den Wert
den Wert
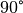 an. In diesem Fall kann der einfallende Lichtstrahl nicht mehr aus
dem optisch dichteren Medium in das optisch dünnere Medium übergehen, sondern
wird reflektiert beziehungsweise verläuft längs der Grenzfläche beider Medien.
Da hierbei
an. In diesem Fall kann der einfallende Lichtstrahl nicht mehr aus
dem optisch dichteren Medium in das optisch dünnere Medium übergehen, sondern
wird reflektiert beziehungsweise verläuft längs der Grenzfläche beider Medien.
Da hierbei 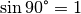 gilt, vereinfacht sich die obige
Gleichung (4) zu folgender Formel:
gilt, vereinfacht sich die obige
Gleichung (4) zu folgender Formel:
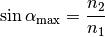
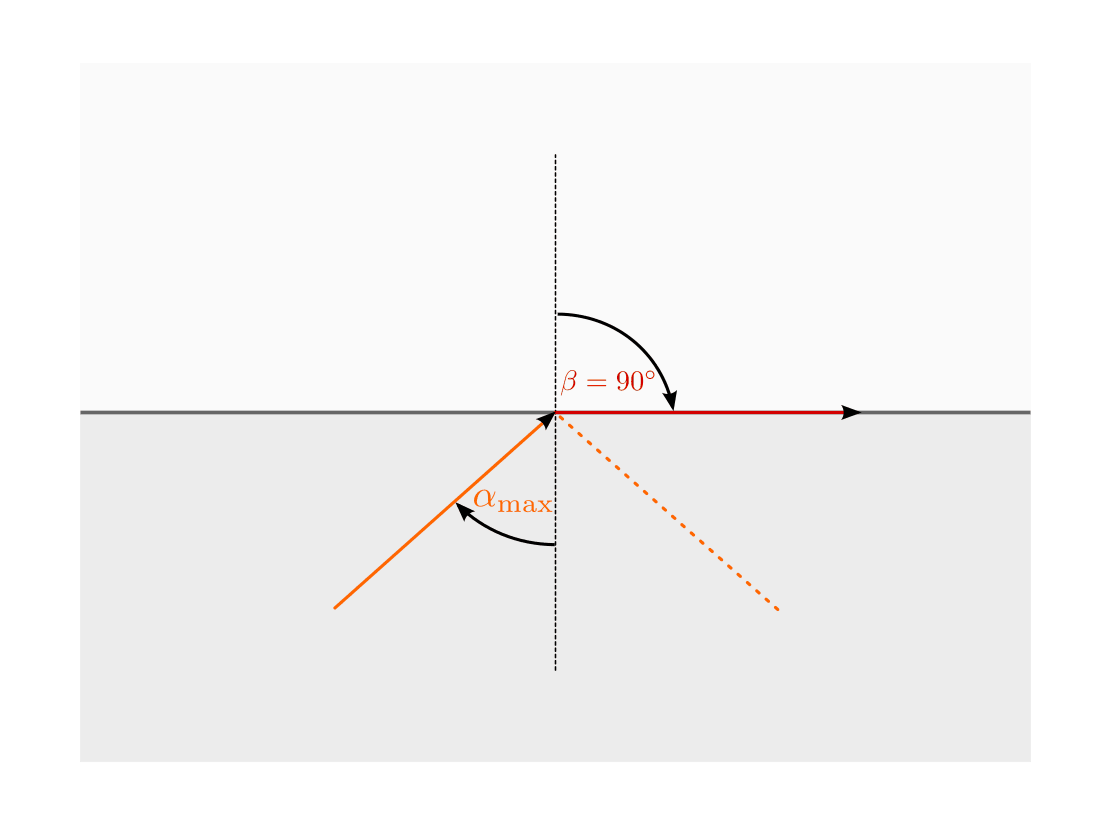
Totalreflexion beim Übergang eines Lichtstrahls von einem optisch dichten in ein optisch dünnes Medium.
Mit Hilfe eines Taschenrechners kann die Umkehrfunktion 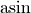 des
Sinus („Arcus-Sinus“) und somit der Grenzwinkel
des
Sinus („Arcus-Sinus“) und somit der Grenzwinkel 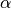 für das Auftreten
von Totalreflexion anhand der beiden Brechzahlen
für das Auftreten
von Totalreflexion anhand der beiden Brechzahlen 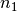 und
und
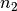 berechnet werden:[3]
berechnet werden:[3]
(5)¶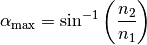
Hierbei ist zu beachten, dass bei der Totalreflexion 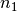 die Brechzahl
des optisch dichteren und
die Brechzahl
des optisch dichteren und 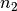 die Brechzahl des optisch dünneren Mediums
bezeichnet, also
die Brechzahl des optisch dünneren Mediums
bezeichnet, also 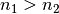 und somit
und somit 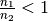 gilt.
Andernfalls kann keine Totalreflexion stattfinden.
gilt.
Andernfalls kann keine Totalreflexion stattfinden.
Beispiel:
- Für den Übergang eines Lichtstrahls von Wasser in Luft ist
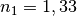 und
und 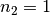 . Somit ergibt
. Somit ergibt 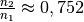 und
und
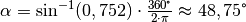 .
. - Für den Übergang eines Lichtstrahls von Quarzglas in Wasser ist
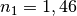 und
und 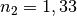 . Somit ergibt
. Somit ergibt 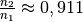 und
und 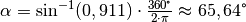 .
.
Je größer der Unterschied der Brechzahlen 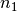 und
und 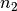 ist, desto
kleiner ist der Grenzwinkel
ist, desto
kleiner ist der Grenzwinkel 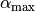 , ab dem Totalreflexion
auftritt. Ist der Einfallswinkel größer als der Grenzwinkel
, ab dem Totalreflexion
auftritt. Ist der Einfallswinkel größer als der Grenzwinkel 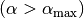 , so wird der Lichtstrahl an der Grenzfläche vollständig
gemäß dem Reflexionsgesetz zurückgeworfen. Diese
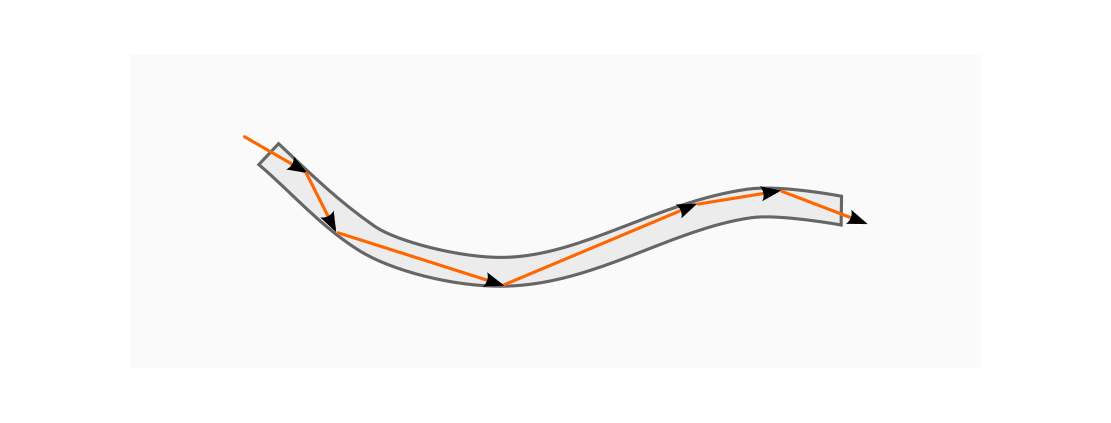
Eigenschaft wird zur Konstruktion von optischen Glasfaser- bzw. Kunstfaserkabeln
als so genannte „Lichtleiter“ genutzt.
, so wird der Lichtstrahl an der Grenzfläche vollständig
gemäß dem Reflexionsgesetz zurückgeworfen. Diese
Eigenschaft wird zur Konstruktion von optischen Glasfaser- bzw. Kunstfaserkabeln
als so genannte „Lichtleiter“ genutzt.
Damit der Einfallswinkel an der Längswand stets groß genug ist, muss ein
Lichtleiter möglichst dünn sein und darf nicht zu stark gebogen werden. Eine
einzelne Faser eines Lichtleiter-Bündels hat meist einen Durchmesser von etwa
![\unit[0,01]{mm}](../_images/math/d0dc41e49194320438c42db838092a1971906332.png) .
.
Doppelte Lichtbrechung an einer ebenen Platte
Beim Durchgang durch eine ebene Platte, beispielsweise eine Glasscheibe, wird ein Lichtstrahl zweimal gebrochen: Beim Eintritt wird der Strahl zur Senkrechten hin, beim Austritt von der Senkrechten weg gebrochen. Da die Brechzahlen und somit die Ablenkungen in beiden Fällen gleich sind, erfährt der Lichtstrahl insgesamt nur eine parallele Verschiebung. In vielen Fällen, insbesondere bei dünnen Scheiben, kann der Effekt vernachlässigt und der doppelt gebrochene Lichtstrahl durch einen einzelnen, geraden Lichtstrahl ersetzt werden.
Eine Totalreflexion kann in diesem Fall nicht
auftreten, da der Austrittswinkel des Lichtstrahls gleich dem Eintrittswinkel
ist und für diesen (von der Senkrechten aus gemessen) stets 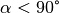 gilt.
gilt.
Doppelte Lichtbrechung an einem Prisma
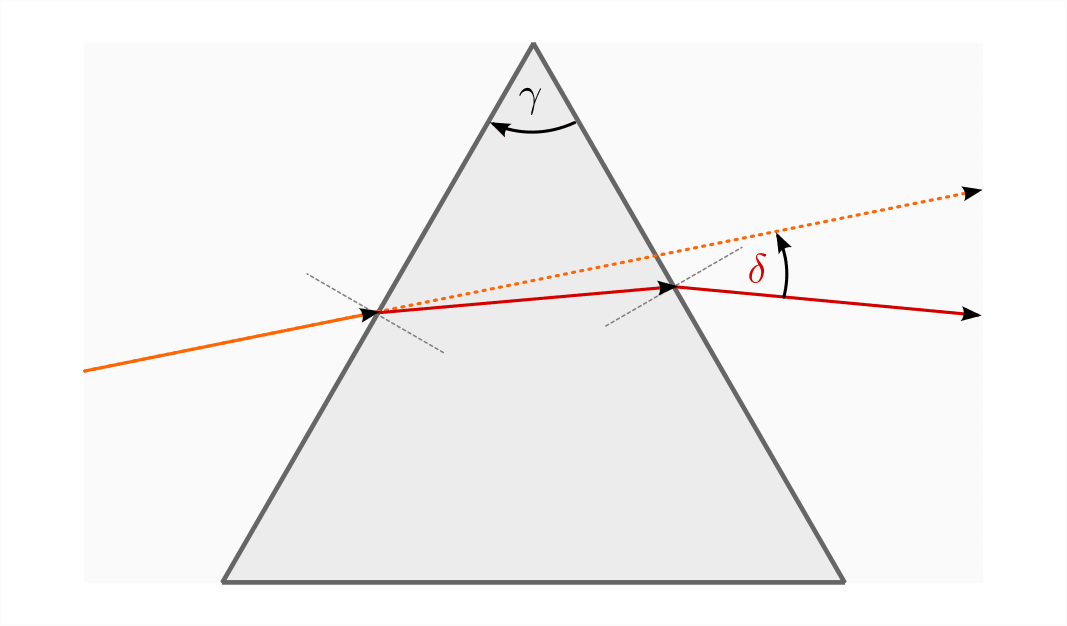
Fällt ein Lichtstrahl auf ein Prisma, so wird er ebenfalls zweimal gebrochen – einmal beim Eintritt in das Prisma (Übergang Luft -> Glas) und ein weiteres mal beim Austritt aus dem Prisma (Übergang Glas -> Luft). Da die beiden Grenzflächen gegeneinander geneigt sind, wird wird der Lichtstrahl insgesamt zum dickeren Ende des Prismas hin abgelenkt.
Umso größer der Keilwinkel 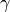 des Prismas ist (d.h. je stumpfer das
Prisma ist), desto stärker ist der Winkel
des Prismas ist (d.h. je stumpfer das
Prisma ist), desto stärker ist der Winkel 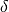 , um den der einfallende
Lichtstrahl abgelenkt wird.
, um den der einfallende
Lichtstrahl abgelenkt wird.
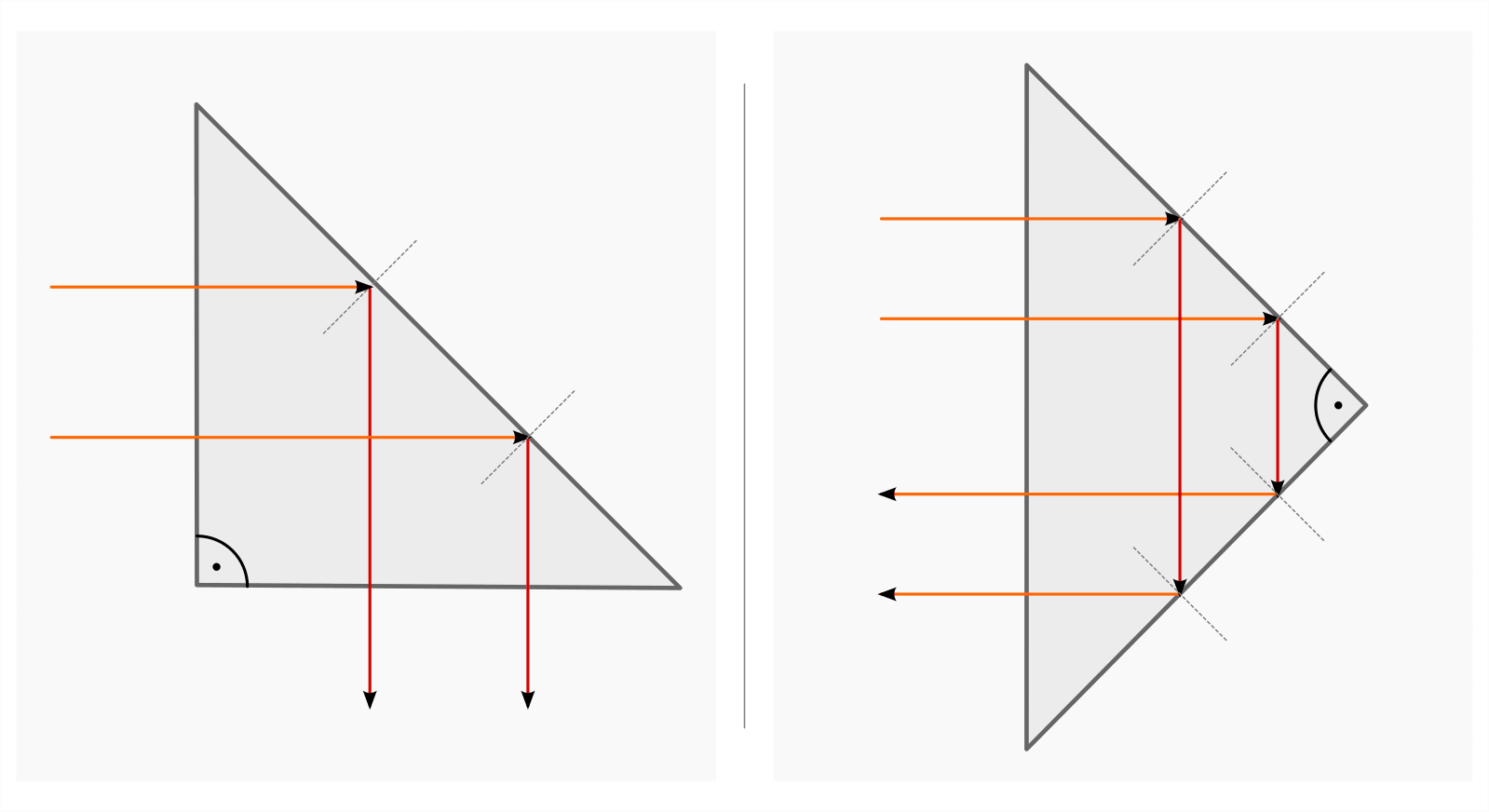
Bei sehr stumpfen Prismen ist sogar eine Totalreflexion des einfallenden Lichts
an dem Lichtstrahl gegenüber liegenden Fläche auftreten. Hierbei kann eine
Ablenkung des Lichts um 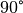 bzw.
bzw. 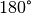 erreicht
werden. Derartige „Umkehrprismen“ werden beispielsweise in Fernrohre oder
Fotokameras eingebaut, um eine Umlenkung bzw. Vertauschung parallel
einfallender Strahlen zu erreichen.
erreicht
werden. Derartige „Umkehrprismen“ werden beispielsweise in Fernrohre oder
Fotokameras eingebaut, um eine Umlenkung bzw. Vertauschung parallel
einfallender Strahlen zu erreichen.
Optische Linsen¶
Geschliffene Gläser können einfallende Lichtstrahlen – je nach Bauform – bündeln oder zerstreuen. Solche glasartigen Körper, die meist kreisförmig sind und eine bestimmte Krümmung aufweisen, werden als „optische Linsen“ bezeichnet. Ein bekanntes Beispiel ist die Lupe, mit deren Hilfe man ein vergrößertes Bild eines Gegenstandes erhalten kann.
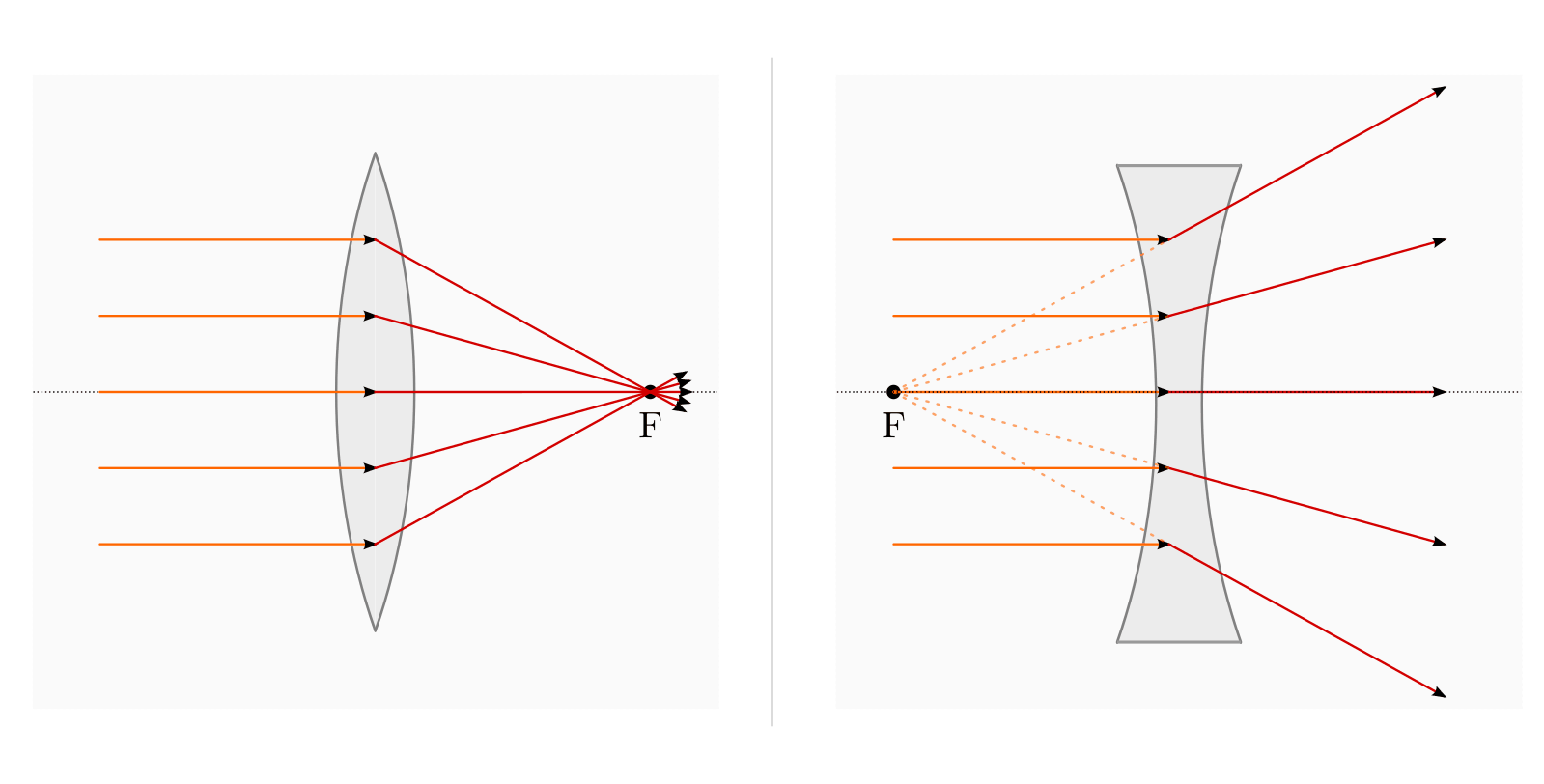
Sammellinse (linkes Bild) und Zerstreuungslinse (rechtes Bild) als typische Formen optischer Linsen.
Um die Bildentstehung an einer optischen Linse zu erklären, verwendet man (weitestgehend) die gleichen Begriffe wie bei der Beschreibung von gekrümmten Spiegeln:
Optische Achse:
Die Gerade, die durch die Mitte der Linse verläuft und senkrecht zur Linsenebene steht, heißt optische Achse.
Parallelstrahlen:
Alle Strahlen, die parallel zur optischen Achse auf eine optische Linse treffen, heißen Parallelstrahlen. Sie werden durch die Linse gesammelt beziehungsweise zerstreut und schneiden sich in einem gemeinsamen Punkt hinter bzw. vor der Linse. Dieser Punkt auf der optischen Achse wird Brennpunkt
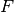 genannt.
genannt.Der Abstand zwischen Linsenmittelpunkt und einem Brennpunkt wird Brennweite
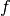 genannt. Die Brennweite einer optischen Linse ist umso größer,
desto flacher die Linse ist.
genannt. Die Brennweite einer optischen Linse ist umso größer,
desto flacher die Linse ist.
Brennpunktstrahlen:
Alle Strahlen, die durch einen Brennpunkt einer optischen Linse verlaufen, werden durch die Linse so gebrochen, dass sie hinter der Linse parallel zur optischen Achse verlaufen.
Mittelpunktstrahlen:
Strahlen, die durch den Linsenmittelpunkt verlaufen, werden beim Eintritt in das Linsenglas ebenso stark gebrochen wie beim Austritt. Mittelpunktstrahlen werden daher nur leicht parallel verschoben (bei dünnen Linsen kaum erkennbar). In guter Näherung durchlaufen Mittelpunktstrahlen die Linse somit unverändert.
Zeichnet man für einen beliebigen Gegenstandspunkt 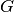 zwei oder drei der
oben genannten Strahlen ein, so erhält man den passenden Bildpunkt als
Schnittpunkt der Strahlen.
zwei oder drei der
oben genannten Strahlen ein, so erhält man den passenden Bildpunkt als
Schnittpunkt der Strahlen.
Bildentstehung an einer Sammellinse
Bei der Abbildung eines Gegenstandes durch eine Sammellinse hängen Lage und
Größe des Bildes von der Entfernung 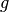 des Gegenstands zur Linse und von
deren Brennweite
des Gegenstands zur Linse und von
deren Brennweite 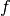 ab.
ab.
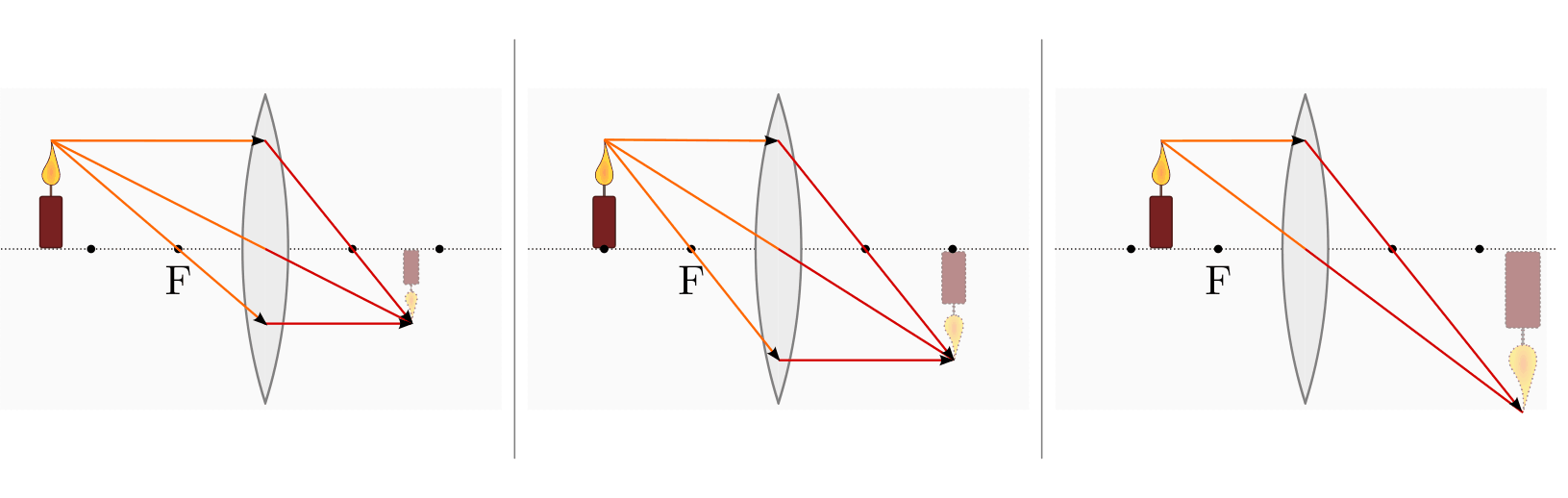
Nähert man einen Gegenstand einer Sammellinse aus weiter Entfernung, so entfernt sich auch das Bild von der Sammellinse. Sammellinsen erzeugen umgekehrte, seitenvertauschte Bilder von Gegenständen, wenn sich diese außerhalb der Brennweite befinden.
Zur Konstruktion des Bildes genügen wiederum die von einem Gegenstandspunkt ausgehenden Brennpunkt- und Parallelstrahlen, die durch die Sammellinse wiederum auf Parallel- bzw. Brennpunktstrahlen abgebildet werden. Der Schnittpunkt der gebrochenen Strahlen entspricht der Lage des Bildes.
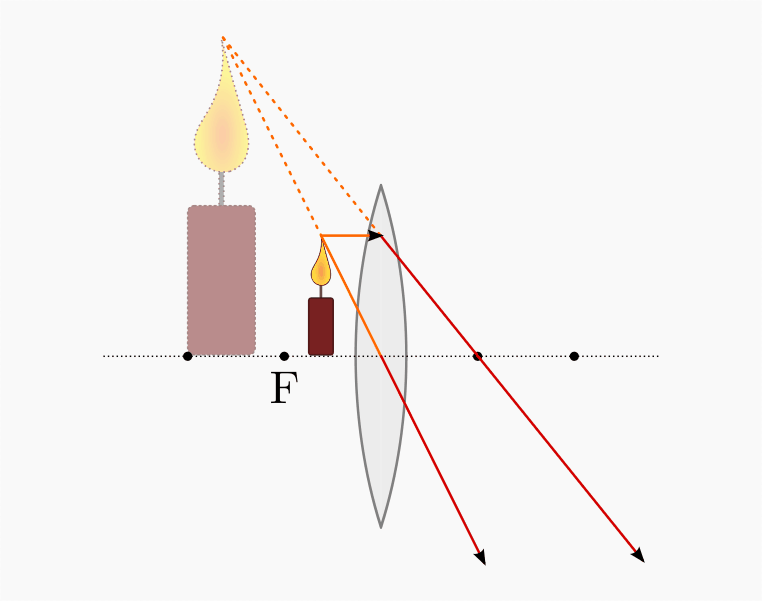
Nähert man einen Gegenstand vom Brennpunkt her einer Sammellinse, so nähert sich auch das Bild der Sammellinse. Sammellinsen erzeugen vergrößerte und aufrechte Bilder der Gegenstände, wenn sie sich innerhalb der Brennweite befinden (Lupeneffekt).
Zur Konstruktion des Bildes zeichnet man die einem Gegenstandspunkt ausgehenden Bildstrahlen hinter der Sammellinse weiter. Dabei ist zu beachten, dass Brennpunktstrahlen zu Parallelstrahlen werden und Mittelpunktstrahlen stets senkrecht auf die Linse treffen und diese somit ohne Lichtbrechung durchlaufen. Die Lage des Bildes entspricht dem Schnittpunkt der so verlängerten Parallel- bzw. Mittelpunktstrahlen hinter dem Gegenstand.
Aufgrund ihrer vergrößernden Wirkung werden flache Sammellinsen (mit einer großen Brennweite) unter anderem als Lupen und Objektive verwendet.
Bildentstehung an einer Zerstreuungslinse
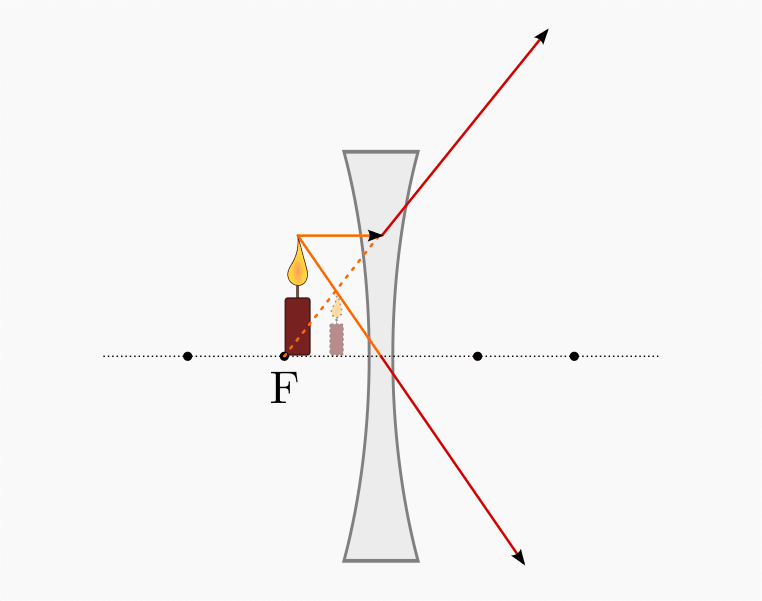
Eine Zerstreuungslinse erzeugt stets aufrechte, verkleinerte Bilder. Nähert man einen Gegenstand an die Linsenoberfläche an, so bewegt sich auch das Bild des Gegenstands auf die Linse zu und wird dabei größer; es bleibt jedoch stets kleiner als das Original.
Zur Konstruktion des Bildes zeichnet man zu einem Gegenstandspunkt wiederum einen Parallel- und einen Brennpunktstrahl ein. Der Parallelstrahl wird durch die Zerstreuungslinse so gebrochen, dass die nach hinten gerichtete Verlängerung des Strahls durch den Brennpunkt verläuft. Das (stets verkleinerte) Bild befindet sich am Schnittpunkt des so verlängerten Parallelstrahls mit dem Mittelpunktstrahl zwischen dem Gegenstand und der Linse.
Anmerkungen:
| [1] | Manchmal wird die Brechzahl auch Brechungsindex genannt. Für kleine Einfallswinkel
Für steilere Einfallswinkel muss hingegen stets mit dem Brechungsgesetz in der allgemeinen Form (3) gerechnet werden. |
| [2] | Transparente Materialien mit einem hoher Brechzahl werden oftmals als „optisch dicht“, Materialien mit einer niedrigeren Brechzahl entsprechend als „optisch dünn“ bezeichnet. |
| [3] | Exakt beträgt die Brechzahl laut Wikipedia (Brechungsindex) von Luft bei
Normalbedingungen 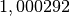 . Starke Temperatur- und
Feuchtigkeitsschwankungen können zu Abweichungen führen und optische Effekte
verursachen (beispielsweise Fata Morgana). . Starke Temperatur- und
Feuchtigkeitsschwankungen können zu Abweichungen führen und optische Effekte
verursachen (beispielsweise Fata Morgana). |
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.

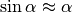 genutzt werden (sofern
genutzt werden (sofern