Lösungen zur Arithmetik¶
Grundrechenarten und Rechenregeln¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Grundrechenarten und Rechenregeln.
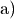 Durch Addition beziehungsweise Subtraktion können nur
gleichartige Terme zusammengefasst werden (beispielsweise ergibt
Durch Addition beziehungsweise Subtraktion können nur
gleichartige Terme zusammengefasst werden (beispielsweise ergibt 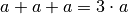 ,
, 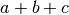 lässt sich hingegen nicht weiter
vereinfachen). Im konkreten Fall müssen zunächst die Klammern aufgelöst
werden:
lässt sich hingegen nicht weiter
vereinfachen). Im konkreten Fall müssen zunächst die Klammern aufgelöst
werden: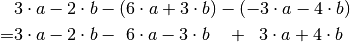
Hierbei wurde berücksichtigt, dass ein Minus-Zeichen vor einer Klammer das Vorzeichen aller Terme innerhalb der Klammer vertauscht. Nun können die einzelnen Vielfachen von
 - beziehungsweise
- beziehungsweise 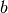 sortiert und
zusammengefasst werden. Man erhält damit
sortiert und
zusammengefasst werden. Man erhält damit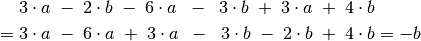
Das Sortieren der einzelnen Summanden ist optional und wird meist nicht explizit geschrieben; im obigen Beispiel wurden die Terme nur zwecks der besseren Übersichtlichkeit explizit sortiert.
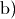 Um Terme miteinander zu multiplizieren, multipliziert man
einerseits die Koeffizienten (mit ihren Vorzeichen) sowie die Variablen
miteinander. Im konkreten Fall ergibt sich damit:
Um Terme miteinander zu multiplizieren, multipliziert man
einerseits die Koeffizienten (mit ihren Vorzeichen) sowie die Variablen
miteinander. Im konkreten Fall ergibt sich damit: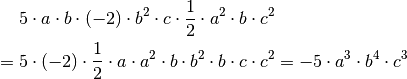
Ebenso wie bei der Multiplikation von Zahlen können somit auch Produkte von gleichartigen Variablen zu Potenzen zusammengefasst werden.
Bruchrechnung¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Bruchrechnung.
Bei der Angabe eines Definitionsbereichs muss sichergestellt werden, dass der Nenner eines Bruchterms nicht Null wird. Konkret muss also gelten:
![\begin{array}{>{\arraybackslash$}p{14cm}<{$} >{\arraybackslash$}p{1cm}<{$}}
\text{a) } \dfrac{5 \cdot a - 3}{4 \cdot a} \qquad \quad \;\;\,
\Rightarrow \; 4 \cdot a \ne 0 \;\,\quad \Longleftrightarrow \quad a
\ne 0 & \\[16pt]
\text{b) } \dfrac{2 \cdot a + 4 \cdot b}{b - 7} \qquad \;\;
\Rightarrow \; b - 7 \ne 0 \quad \Longleftrightarrow \quad b \ne 7 &
\\[16pt]
\text{c) } \dfrac{8}{(c + 3) \cdot (c - 2)} \;\;\; \Rightarrow \;
(c+3) \ne 0 \text{ und } (c-2) \ne 0 \quad \Longleftrightarrow \quad c
\ne -3 \; \wedge \; c \ne 2 & \\[18pt]
\text{d) } \dfrac{2 \cdot c \, + \, 5 \cdot d \, + \, 1}{3 \cdot
d\;\!^2 + 1} \; \Rightarrow \; d\;\!^2 > -1 \; \quad
\Longleftrightarrow \quad \text{ keine Einschränkung nötig!} &
\\[12pt]
\end{array}](../_images/math/525f6d3d9545f38d70a3ef7ab01cb6cbebeba751.png)
In Teilaufgabe
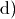 wurde die Tatsache genutzt, dass das Quadrat
einer Zahl stets positiv ist.
wurde die Tatsache genutzt, dass das Quadrat
einer Zahl stets positiv ist.
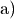 Die beiden Bruchterme haben den gleichen Nenner; folglich
lassen sich ihre Zähler unmittelbar zusammenfassen:
Die beiden Bruchterme haben den gleichen Nenner; folglich
lassen sich ihre Zähler unmittelbar zusammenfassen: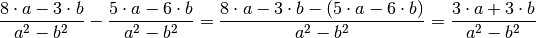
Im Zähler kann nun
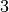 als gemeinsamer Faktor ausgeklammert werden; der
Nenner kann als binomische Formel geschrieben werden. Damit ergibt sich:
als gemeinsamer Faktor ausgeklammert werden; der
Nenner kann als binomische Formel geschrieben werden. Damit ergibt sich: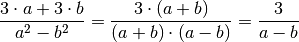
Im letzten Rechenschritt wurde der gemeinsame Faktor
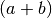 gekürzt.
gekürzt.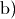 Bei dem Produkt der beiden Bruchterme kann der Faktor
Bei dem Produkt der beiden Bruchterme kann der Faktor
 gekürzt werden; ebenso kann der verbleibende Zählerterm
gekürzt werden; ebenso kann der verbleibende Zählerterm
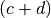 gegen das Quadrat dieses Terms im Nenner gekürzt werden. Damit
ergibt sich:
gegen das Quadrat dieses Terms im Nenner gekürzt werden. Damit
ergibt sich: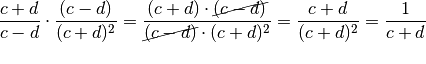
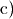 Dividieren heißt mit dem Kehrbruch multiplizieren. Damit
ergibt sich:
Dividieren heißt mit dem Kehrbruch multiplizieren. Damit
ergibt sich: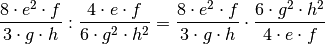
Dieses Produkt enthält sowohl im Zähler wie auch im Nenner ausschließlich Produkte; die einzelnen Faktoren können somit folgendermaßen gekürzt werden:
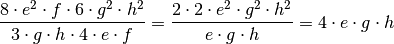
Potenzen, Wurzeln und Logarithmen¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Potenzen, Wurzeln und Logarithmen.
 Die Wurzel kann folgendermaßen umgestellt werden:
Die Wurzel kann folgendermaßen umgestellt werden:![\sqrt[2]{16}^3 = 16^{\frac{3}{2}} = (\sqrt[2]{16})^3 = 4^3 = 64](../_images/math/962ff5ddf66411e086830164dd5602d88442b553.png)
 Beim Quadrieren eines Produkts werden alle Faktoren einzeln
quadriert, es gilt also
Beim Quadrieren eines Produkts werden alle Faktoren einzeln
quadriert, es gilt also 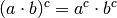 . Man erhält
damit:
. Man erhält
damit: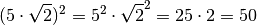
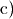 In der Darstellung als allgemeine Potenz ergibt sich für
die Wurzel:
In der Darstellung als allgemeine Potenz ergibt sich für
die Wurzel:![(\sqrt[2]{7})^4 = 7^{\frac{4}{2}} = 7^2 = 49](../_images/math/c64b78673a1127e95b3b21d62e292f7755232246.png)
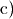 Auch in diesem Fall ist eine Darstellung der Wurzel als
allgemeine Potenz hilfreich. Mit dem Zusammenhang
Auch in diesem Fall ist eine Darstellung der Wurzel als
allgemeine Potenz hilfreich. Mit dem Zusammenhang 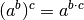 ergibt sich:
ergibt sich:![\sqrt[4]{a^8 \cdot b^4}^3 = (a^8 \cdot b^4)^{\frac{3}{4}} = a ^{8 \cdot
\frac{3}{4}} \cdot b^{4 \cdot \frac{3}{4}} = a^6 \cdot b^3 \\[12pt]](../_images/math/adcccff1fa0d87a44537abbb69637aadc1b74b0b.png)
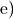 Der Term lässt sich vereinfachen, indem man die einzelnen
Wurzeln schrittweise „zusammenzieht“:
Der Term lässt sich vereinfachen, indem man die einzelnen
Wurzeln schrittweise „zusammenzieht“:![\sqrt[3]{7 \cdot \sqrt{7 \cdot \sqrt[3]{7}}} = \sqrt[3]{7 \cdot
\sqrt{\sqrt[3]{7^3 \cdot 7}}} = \sqrt[3]{7 \cdot \sqrt[6]{7^4}} =
\sqrt[3]{7 \cdot \sqrt[3]{7^2}} = \sqrt[3]{\sqrt[3]{7^3 \cdot 7^2}} =
\sqrt[9]{7^5}](../_images/math/d310c148c6b18c384d19a981cbadd3e6862ff39c.png)
Im ersten Schritt wurde für der Faktor
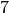 durch den gleichwertigen
Ausdruck
durch den gleichwertigen
Ausdruck ![\sqrt[3]{7^3}](../_images/math/924dfd5ec06cb138e3089ab72f83670a6ea6d9f1.png) ersetzt und damit das Produkt der Wurzeln
ersetzt und damit das Produkt der Wurzeln
![\sqrt[3]{7^3} \cdot \sqrt[3]{7}](../_images/math/7d9892df2ea5252aef629fb74ed54a55ac03e1a9.png) zu einer Wurzel
zu einer Wurzel ![\sqrt[3]{7^3
\cdot 7}](../_images/math/678c346ccb68ff08e75ec2cc106664df66549cac.png) zusammengefasst. Dadurch konnte die Quadrat- und die innere
Kubikwurzel als eine einzige Wurzel geschrieben werden. Ein ähnliches Vorgehen
wurde dann nochmals angewendet.
zusammengefasst. Dadurch konnte die Quadrat- und die innere
Kubikwurzel als eine einzige Wurzel geschrieben werden. Ein ähnliches Vorgehen
wurde dann nochmals angewendet.Eine alternative, vielleicht übersichtlichere Schreibweise erhält man, wenn man die einzelnen Wurzeln als allgemeine Potenzen darstellt:
![\sqrt[3]{7 \cdot \sqrt{7 \cdot \sqrt[3]{7}}} = \left( 7 \cdot \left( 7
\cdot 7^{\frac{1}{3}} \right)^{\frac{1}{2}} \right)^{\frac{1}{3}} = \left(
7 \cdot \left( 7^{\frac{4}{3}} \right)^{\frac{1}{2}} \right)^{\frac{1}{3}}
= \left( 7 \cdot 7^{\frac{2}{3}} \right)^{\frac{1}{3}} = \left(
7^{\frac{5}{3}} \right)^{\frac{1}{3}} = 7^{\frac{5}{9}} \\
{\color{white}...}](../_images/math/ac0c408d5d1eac31d3186759ed0d171fe2187d66.png)
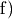 Zunächst kann man das Minus im Exponenten beseitigen, indem
man Zähler und Nenner vertauscht:
Zunächst kann man das Minus im Exponenten beseitigen, indem
man Zähler und Nenner vertauscht:![\left( \dfrac{\sqrt[3]{3}}{\sqrt[2]{6}} \right)^{-6} = \left(
\dfrac{\sqrt[2]{6}}{\sqrt[3]{3}} \right)^6](../_images/math/a81db7ccd65d13e433dc6c1d1cf93aba2e0e987e.png)
Für eine weitere Vereinfachung ist es empfehlenswert, die Wurzeln als allgemeine Potenzen darzustellen und den Zusammenhang
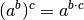 zu nutzen:
zu nutzen:![\left( \dfrac{\sqrt[2]{6}}{\sqrt[3]{3}} \right)^6 = \left(
\frac{6^{\frac{1}{2}}}{ 3^{\frac{1}{3}}} \right)^6 = \frac{6^{\frac{1}{2}
\cdot 6}}{ 3 ^{\frac{1}{3} \cdot 6}} = \frac{6^3}{3^2} = 24](../_images/math/efd527d5faa80df965aeae9bb94e2cfc3113a641.png)
