Eigenschaften von Gleichungen¶
Eine Gleichung entspricht einer Aussageform, bei der zwei
Terme 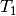 und
und 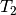 durch die Gleichheits-Relation
durch die Gleichheits-Relation
 miteinander verbunden sind:
miteinander verbunden sind:
(1)¶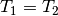
Als Aussageform ist eine Variablengleichung weder wahr noch falsch. Belegt man
allerdings die Variablen mit zulässigen Werten, so nehmen die einzelnen Terme
bestimmte Werte an – die Gleichung wird hierbei zu einer wahren oder falschen
Aussage.[1] Ergibt sich eine wahre Aussage, so wird die Gleichung durch die
eingesetzten Zahlen erfüllt. Diese Zahlen werden als Lösungen der Gleichung
bezeichnet, die Gesamtheit aller Lösungen wird Lösungsmenge 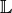 genannt.
genannt.
Im einfachsten Fall entsprechen die beiden Terme 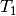 und
und 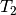 zwei einzelnen Elementen
zwei einzelnen Elementen 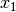 und
und 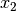 einer Menge
einer Menge
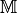 . Diese können entweder gleich
. Diese können entweder gleich 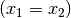 oder
ungleich
oder
ungleich 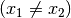 sein. Im ersten Fall stehen die Variablen
sein. Im ersten Fall stehen die Variablen
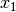 und
und 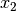 für das selbe Objekt.
für das selbe Objekt.
Lösbarkeit von Gleichungen¶
Ob eine Gleichung lösbar ist, hängt von der Gleichung selbst sowie von dem
vorgegebenen Variablenbereich („Definitionsmenge“ 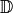 ) ab.
) ab.
- Ist die Lösungsmenge leer
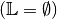 , so ist die
Gleichung bezüglich
, so ist die
Gleichung bezüglich 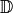 unerfüllbar.
unerfüllbar. - Ist die Lösungsmenge gleich der Definitionsmenge
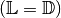 , so ist die Gleichung bzgl.
, so ist die Gleichung bzgl. 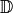 stets erfüllt
(„allgemeingültig“).
stets erfüllt
(„allgemeingültig“). - Grundsätzlich ist die Lösungsmenge eine Teilmenge der Definitionsmenge
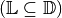 .
.
Allgemeingültige Gleichungen (auch „Identitäten“ genannt) werden oftmals als
Rechenregeln verwendet, da sie unabhängig vom Wert der Variablen stets wahr sind
und somit zur Vereinfachung einzelner Terme genutzt werden können. Gilt nämlich
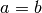 , so kann in jeder Aussage nach Belieben
, so kann in jeder Aussage nach Belieben  durch
durch 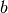 ersetzt werden (Ersetzbarkeits-Theorem von Leibniz).
ersetzt werden (Ersetzbarkeits-Theorem von Leibniz).
Ebenfalls können nach diesem Prinzip auch zwei Terme, die jeweils mit einem
dritten übereinstimmen, gleichgesetzt werden. Gilt nämlich 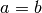 und
und
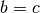 , so folgt aus der Äquivalenz der
Gleichheitsrelation automatisch auch
, so folgt aus der Äquivalenz der
Gleichheitsrelation automatisch auch  :
:
(2)¶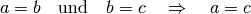
Bei algebraischen Aufgaben muss die Lösungsmenge einer Gleichung meist erst bestimmt werden. Als Unterscheidung zu den stets wahren Identitäten werden derartige Gleichungen, deren Lösungsmenge erst gefunden werden muss, auch „Bestimmungsgleichungen“ genannt.
Beispiele:
Folgende Gleichung ist für jede reelle Zahl
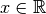 unerfüllbar:
unerfüllbar: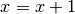
Für die Lösungsmenge gilt somit
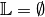 .
.Folgende Gleichung ist für jede reelle Zahl
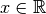 allgemeingültig:
allgemeingültig: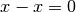
Für die Lösungsmenge gilt somit
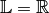 .
.Folgende Gleichung liefert nicht für jedes
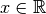 eine wahre Aussage:
eine wahre Aussage: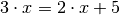
Die Lösungsmenge ist somit eine Teilmenge des Definitionsbereichs. Konkret gilt
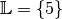 .
.
Ist die Lösungsmenge einer Gleichung nicht unmittelbar erkennbar, so kann diese durch entsprechende Umformungen in eine einfacher zu lösende Form gebracht werden.
Äquivalentes Umformen von Gleichungen¶
Manchmal lässt sich die Lösungsmenge einer Gleichung durch Einsetzen von konkreten Werten in die Variablen („Probieren“) ermitteln. Im Allgemeinen jedoch muss man eine Gleichung durch schrittweises Umformen lösen. Wesentlich hierfür ist in diesem Zusammenhang die Äquivalenz von Gleichungen.
Eine Gleichung heißt äquivalent (gleichwertig) zu einer anderen Gleichung, wenn
beide die gleiche Lösungsmenge 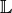 bei gleicher Definitionsmenge
bei gleicher Definitionsmenge
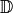 besitzen. Eine Umformung, durch die eine Gleichung in eine zu
ihr äquivalente Gleichung übergeht, heißt äquivalente Umformung. Beispielsweise
dürfen aufgrund der Symmetrie der Gleichheits-Relation stets die linke und die
rechte Seite einer Gleichung vertauscht werden:
besitzen. Eine Umformung, durch die eine Gleichung in eine zu
ihr äquivalente Gleichung übergeht, heißt äquivalente Umformung. Beispielsweise
dürfen aufgrund der Symmetrie der Gleichheits-Relation stets die linke und die
rechte Seite einer Gleichung vertauscht werden:
(3)¶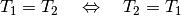
Termumformungen, die sich nur auf eine Seite einer Gleichung auswirken, beispielsweise Zusammenfassen und Ausmultiplizieren beziehungsweise Ausklammern von Summentermen sowie Kürzen und Erweitern von Bruchtermen, dürfen ebenso jederzeit vorgenommen werden.
Addiert oder subtrahiert man auf beiden Seiten einen beliebigen Term 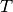 ,
so ist die neue Gleichung äquivalent zur ursprünglichen. Der Wahrheitswert einer
Gleichung bleibt auch unverändert, wenn beiden Seiten mit einem Term
,
so ist die neue Gleichung äquivalent zur ursprünglichen. Der Wahrheitswert einer
Gleichung bleibt auch unverändert, wenn beiden Seiten mit einem Term 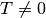 multipliziert oder durch einen solchen dividiert werden. Somit gilt:[2]
multipliziert oder durch einen solchen dividiert werden. Somit gilt:[2]
(4)¶
Während eine Addition oder Subtraktion eines beliebigen Terms auf beiden Seiten
der Gleichung jederzeit problemlos möglich ist, ist bei der Multiplikation einer
Gleichung mit einem Term beziehungsweise der Division durch einen Term 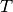 stets Vorsicht geboten. Wird hierbei die Bedingung
stets Vorsicht geboten. Wird hierbei die Bedingung 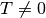 nicht
beachtet, so können in der neuen Gleichung zusätzliche Lösungen hinzukommen
beziehungsweise ursprünglich gültige Lösung verschwinden.
nicht
beachtet, so können in der neuen Gleichung zusätzliche Lösungen hinzukommen
beziehungsweise ursprünglich gültige Lösung verschwinden.
Beispiele:
Die Gleichung
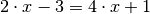 hat, wie man durch
Einsetzen überprüfen kann, die Lösungsmenge
hat, wie man durch
Einsetzen überprüfen kann, die Lösungsmenge 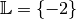 .
Multipliziert man beide Seiten mit
.
Multipliziert man beide Seiten mit 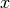 , so erhält man folgende
Gleichung:
, so erhält man folgende
Gleichung: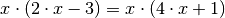
Die neue Gleichung hat neben der ursprünglichen Lösung
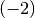 auch
die Lösung
auch
die Lösung 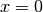 ; die Lösungsmenge der neuen Gleichung ist also
; die Lösungsmenge der neuen Gleichung ist also
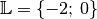 . Somit ist die neue Gleichung
nicht äquivalent zur ursprünglichen Gleichung.
. Somit ist die neue Gleichung
nicht äquivalent zur ursprünglichen Gleichung.Die Gleichung
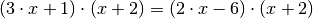 hat, wie man durch Einsetzen überprüfen kann, die Lösungsmenge
hat, wie man durch Einsetzen überprüfen kann, die Lösungsmenge
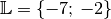 . Teilt man beide Seiten der Gleichung
durch den Term
. Teilt man beide Seiten der Gleichung
durch den Term 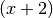 , so erhält man folgende Gleichung:
, so erhält man folgende Gleichung: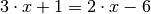
Die neue Gleichung hat die Lösungsmenge
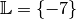 ; bei der
Division ist die zweite ursprüngliche Lösung
; bei der
Division ist die zweite ursprüngliche Lösung 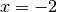 entfallen. Somit
ist die neue Gleichung nicht äquivalent zur ursprünglichen Gleichung.
entfallen. Somit
ist die neue Gleichung nicht äquivalent zur ursprünglichen Gleichung.
Die äquivalenten Umformungs-Verfahren von Gleichungen beziehen sich auf die Anwendung der vier grundlegenden Rechenoperationen (Addition, Subtraktion, Multiplikation und Division). Werden weitere Rechenoperationen (beispielsweise Potenzieren, Wurzelziehen oder Logarithmieren) angewendet, sind oft zusätzliche Überlegungen nötig.
Eine Kontrolle der Lösungsmenge kann durch Einsetzen der Elemente in die Ausgangsgleichung („Probe“) erfolgen. Bei einer Probe ist jede Gleichungsseite getrennt auszurechnen, es dürfen also keine Gleichungsumformungen vorgenommen werden.
Anmerkungen:
| [1] | Tritt eine Variable in einem Term beziehungsweise in einer Gleichung mehrfach auf, so muss sie beim Ersetzen durch einen konkreten Wert an jeder Stelle durch ein und den selben Wert ersetzt werden. In Termen oder Gleichungen mit mehreren Variablen können unterschiedliche Variablen mit beliebigen (gleichen oder verschiedenen) Werten belegt werden. |
| [2] | 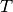 ist eine Zahl oder ein Term, der für alle Elemente des
Definitionsbereichs der Ausgangsgleichung ist eine Zahl oder ein Term, der für alle Elemente des
Definitionsbereichs der Ausgangsgleichung 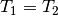 definiert sein
muss. definiert sein
muss. |

![T_1 = T_2 \quad &\Leftrightarrow \quad T_1 + T = T_2 + T \\[2pt]
T_1 = T_2 \quad &\Leftrightarrow \quad T_1 - T = T_2 - T \\[2pt]
%\phantom{\qquad (T \ne 0) T + + T}
T_1 = T_2 \quad &\Leftrightarrow \quad T_1 \, \cdot \; T = T_2 \, \cdot
\; T \qquad (T \ne 0)\\[2pt]
T_1 = T_2 \quad &\Leftrightarrow \quad T_1 \, : \, T = T_2 \, : \, T
\qquad (T \ne 0)](../../_images/math/d61918769ca8958e698f7b262de1b5aa50784a76.png)