Reihen- und Parallelschaltungen¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Reihen- und Parallelschaltungen.
Reihen- und Parallelschaltungen von Stromquellen
Bei einer Reihenschaltung von
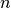 Stromquellen addieren sich die Werte
der Spannungen
Stromquellen addieren sich die Werte
der Spannungen 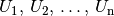 zu einer
Gesamtspannung
zu einer
Gesamtspannung 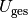 . Wenn drei Batterien mit einer
Spannung von je
. Wenn drei Batterien mit einer
Spannung von je ![\unit[1,5]{V}](../_images/math/cd0d3af24b03bcdd8aad5e9a0a694d1c1ff551d7.png) in Reihe geschaltet werden, ergibt sich
somit folgende Gesamt-Spannung:
in Reihe geschaltet werden, ergibt sich
somit folgende Gesamt-Spannung:![U_{\mathrm{ges}} &= U_1 + U_2 + U_3 = \unit[1,5]{V} + \unit[1,5]{V} +
\unit[1,5]{V} = \unit[4,5]{V}](../_images/math/64ec44abc173879877dbdc7ba41f4d0c46771170.png)
Bei einer Parallelschaltung von (gleichartigen) Stromquellen ist die Gesamtspannung gleich der Spannung einer einzelnen Stromquelle.[1] Eine Parallelschaltung zweier
![\unit[1,5]{V}](../_images/math/cd0d3af24b03bcdd8aad5e9a0a694d1c1ff551d7.png) -Batterien liefert somit eine
Gesamt-Spannung von ebenfalls
-Batterien liefert somit eine
Gesamt-Spannung von ebenfalls ![\unit[1,5]{V}](../_images/math/cd0d3af24b03bcdd8aad5e9a0a694d1c1ff551d7.png) .
.
Reihen- und Parallelschaltungen von Widerständen
Bei einer Reihenschaltung von Widerständen treten keine Verzweigungen auf; in jeden Netzwerk-Knoten fließt somit gleich viel Strom hinein, wie aus ihm auch wieder hinausfließt. Es gilt somit
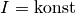 an allen Stellen in
der Schaltung.
an allen Stellen in
der Schaltung.Eine Reihenschaltung bildet zudem gemeinsam mit der Spannungsquelle eine Masche. Innerhalb dieser Masche ergeben alle Spannungen in Summe Null. Nach dem Ohmschen Gesetz gilt:
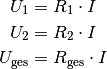
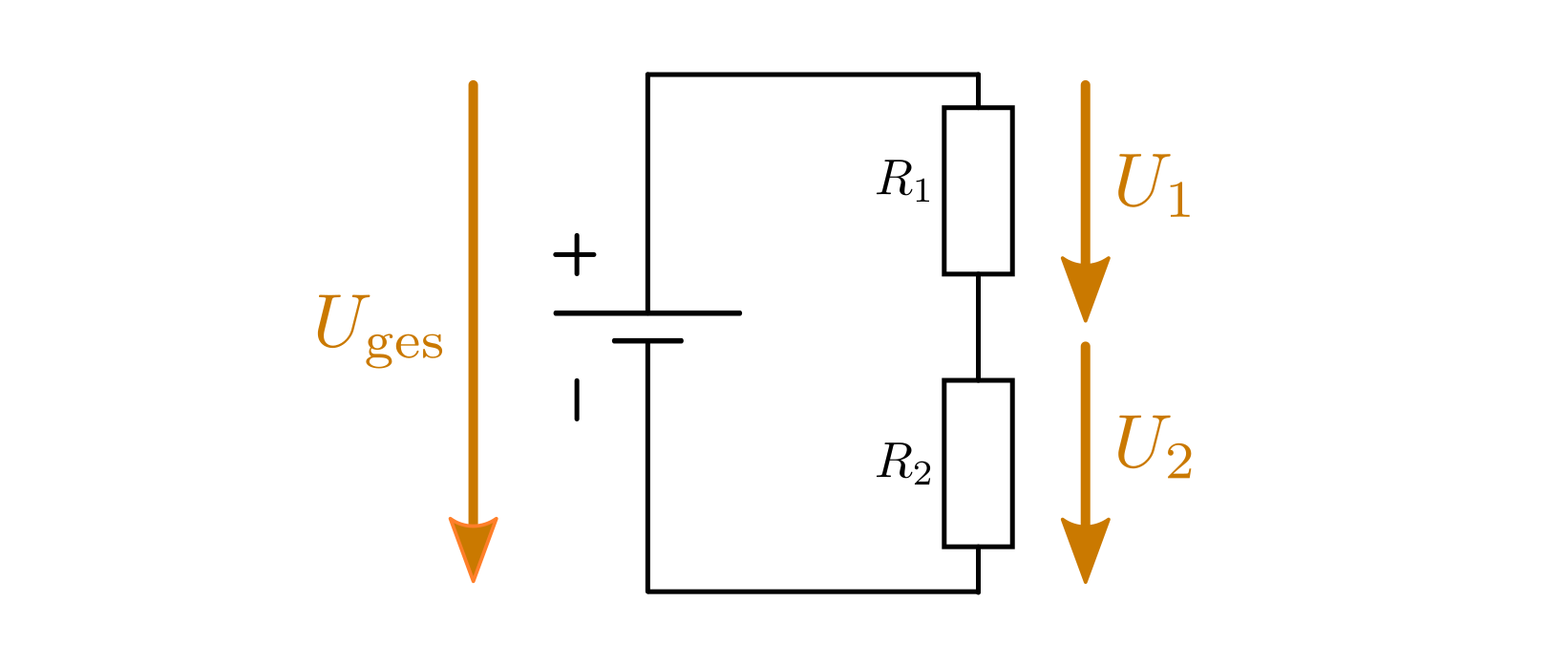
SVG: Netzwerk-Knoten (Loesung)Aus der Maschenregel ergibt sich:
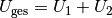
Setzt man die aus dem Ohmschen Gesetz resultierenden Ausdrücke in diese Gleichung ein, so erhält man:
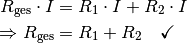
Die Formel
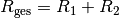 für die Reihenschaltung zweier
Widerstände folgt somit unmittelbar aus dem Ohmschen Gesetz sowie der
Kirchhoffschen Maschenregel.
für die Reihenschaltung zweier
Widerstände folgt somit unmittelbar aus dem Ohmschen Gesetz sowie der
Kirchhoffschen Maschenregel.
In einer Parallelschaltung ist die Gesamt-Stromstärke
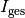 gleich der Summe der (Teil-)Stromstärken
gleich der Summe der (Teil-)Stromstärken 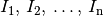 . Betragen die Stromstärken
. Betragen die Stromstärken 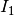 und
und 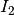 in zwei
Stromzweigen
in zwei
Stromzweigen ![\unit[1,8]{A}](../_images/math/c72ea2dc51d44dba311c753c0d426e0b8b592e08.png) bzw.
bzw. ![\unit[2,2]{A}](../_images/math/d5c0950bdc5742671ea40cebf41a75afddb599b4.png) , so ergibt sich
damit folgende Gesamt-Stromstärke:
, so ergibt sich
damit folgende Gesamt-Stromstärke:![I_{\mathrm{ges}} = I_1 + I_2
= \unit[1,8]{A} + \unit[2,2]{A} = \unit[4,0]{A}](../_images/math/01bec08971aafa41c4f869243425cb6ce0d9a4ce.png)
Die Gesamt-Stromstärke beträgt somit
![I_{\mathrm{ges}} = \unit[4,0]{A}](../_images/math/f720c3c4116565666b0401b43f6ef440b5819969.png) .
.
Bei einer Reihenschaltung ist der Gesamtwiderstand
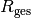 gleich der Summe der einzelnen Widerstandswerte; für eine Reihenschaltung
zweier Widerstände
gleich der Summe der einzelnen Widerstandswerte; für eine Reihenschaltung
zweier Widerstände ![R_1 = \unit[100]{\Omega }](../_images/math/765718886c822c300c5a329d7d8965dc29065630.png) und
und ![R_2 =
\unit[50]{\Omega }](../_images/math/9131a934f765a0aacf3e303cee3b44c01ee9553f.png) gilt somit:
gilt somit:![R_{\mathrm{ges}} = R_1 + R_2 = \unit[100]{\Omega } + \unit[50]{\Omega } =
\unit[150]{\Omega }](../_images/math/71448c8e0312e13006bbaaabd572427e2e50fb1b.png)
Durch Einsetzen des Werts der anliegenden Spannung
![U_{\mathrm{ges}} =
\unit[9]{V}](../_images/math/4c8269fc46a04ee7c7148bea9711f761cb78d75f.png) und des Gesamtwiderstandes
und des Gesamtwiderstandes ![R_{\mathrm{Ges}} =
\unit[150]{\Omega}](../_images/math/4e71cf8fc29fa74be607df17268154ca7ece8a76.png) in das Ohmsche Gesetz
in das Ohmsche Gesetz 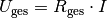 folgt damit für die fließende Stromstärke
folgt damit für die fließende Stromstärke 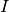 :
: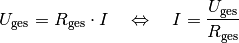
![I = \frac{U_{\mathrm{ges}}}{R_{\mathrm{ges}}} =
\frac{\unit[9]{V}}{\unit[150]{\Omega}} = \unit[0,06]{A} = \unit[60]{mA}](../_images/math/8a6cd52dc4c8f5b1fdd94534f44baa6cf4967365.png)
Die Stromstärke beträgt somit
![I = \unit[60]{mA}](../_images/math/7e37bf18d01eb9b10efdb9593365e66dd33571f1.png) (an allen Stellen
der Reihenschaltung). Wiederum mit Hilfe des Ohmschen Gesetzes können damit
die beiden Teilspannungen
(an allen Stellen
der Reihenschaltung). Wiederum mit Hilfe des Ohmschen Gesetzes können damit
die beiden Teilspannungen 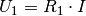 und
und 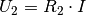 an den beiden Widerständen berechnet werden:
an den beiden Widerständen berechnet werden:![U_1 &= R_1 \cdot I = \unit[100]{\Omega} \cdot \unit[0,06]{A} = \unit[6]{V}
\\[6pt]
U_2 &= R_1 \cdot I = \unit[50]{\Omega} \cdot \unit[0,06]{A} = \unit[3]{V}](../_images/math/337902fa63a375e37b9d5a8c34e2c3eacc05a2a7.png)
Die beiden Teilspannungen
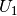 und
und 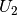 betragen somit
betragen somit
![\unit[6]{V}](../_images/math/96456f72a188a973330fe6e04ec5db948076876c.png) bzw.
bzw. ![\unit[3]{V}](../_images/math/bbb363d2c6e80babe898c73e95016fba9d64e015.png) . In der Summe ergeben sie die
Gesamtspannung
. In der Summe ergeben sie die
Gesamtspannung ![U_{\mathrm{ges}} = \unit[9]{V}](../_images/math/b9e5cd20159ad9c1edd1ac66b4ba20df5fd58ab1.png) , zueinander stehen sie
im gleichen Verhältnis wie die Werte
, zueinander stehen sie
im gleichen Verhältnis wie die Werte 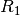 und
und 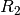 der
Widerstände
der
Widerstände 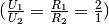 .
.
Bei einer Parallelschaltung ist der Kehrwert des Gesamtwiderstands
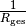 gleich der Summe der Kehrwerte der
einzelnen Widerstandswerte; für eine Reihenschaltung zweier Widerstände
gleich der Summe der Kehrwerte der
einzelnen Widerstandswerte; für eine Reihenschaltung zweier Widerstände
![R_1 = \unit[100]{\Omega }](../_images/math/765718886c822c300c5a329d7d8965dc29065630.png) und
und ![R_2 = \unit[50]{\Omega }](../_images/math/a752085645cb717fce54b71371860f7b6febbf4f.png) gilt
somit:
gilt
somit:![\frac{1}{R_{\mathrm{ges}}} = \frac{1}{R_1} + \frac{1}{R_2} =
\frac{1}{\unit[100]{\Omega }} + \frac{1}{\unit[50]{\Omega }} =
\unit[\frac{3}{100} ]{\frac{1}{\Omega }}](../_images/math/9c9cf70ccbf4501b810c0f21debabfbcba68ac48.png)
![\Rightarrow R_{\mathrm{ges}} = \unit[\frac{100}{3}]{\Omega } \approx
\unit[33,3]{\Omega }](../_images/math/1216fcede87d2152d8466144f4b0ba87d2f847a8.png)
Durch Einsetzen des Werts der anliegenden Spannung
![U = \unit[9]{V}](../_images/math/3ee4ddce6280e2707c96845d95a394815f2bbcfc.png) und des Gesamtwiderstandes
und des Gesamtwiderstandes ![R_{\mathrm{Ges}} = \unit[33,3]{\Omega }](../_images/math/b22aad8098dabe9295e52246f444b1b6e57eea05.png) in
das Ohmsche Gesetz
in
das Ohmsche Gesetz 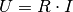 folgt damit für die im
unverzweigten Teil fließende Stromstärke
folgt damit für die im
unverzweigten Teil fließende Stromstärke 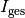 :
: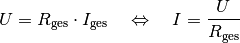
![I_{\mathrm{ges}} = \frac{U}{R_{\mathrm{ges}}} =
\frac{\unit[9]{V}}{\unit[33,3]{\Omega }} = \unit[0,27]{A} =
\unit[270]{mA}](../_images/math/8d3c22715cbd262b5e429786af227b4d45b516bc.png)
Die Stromstärke beträgt im unverzweigten Teil der Schaltung somit
![I =
\unit[270]{mA}](../_images/math/0d01640276f473b918ebf627e0804b6ccf6259b7.png) .
.
Bei einer Parallelschaltung lässt sich der Kehrwert des Gesamtwiderstands
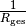 als Summe der Kehrwerte der einzelnen
Widerstandswerte berechnen:
als Summe der Kehrwerte der einzelnen
Widerstandswerte berechnen:![\frac{1}{R_{\mathrm{ges}}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} =
\frac{1}{\unit[100]{\Omega }} + \frac{1}{\unit[470]{\Omega }} +
\frac{1}{\unit[1\,000]{\Omega }} \approx \unit[0,013]{\frac{1}{\Omega } }](../_images/math/f68eff3f36b1efa238acdd1ddbda20153098a3ef.png)
![\Rightarrow R_{\mathrm{ges}} \approx \unit[76,2]{\Omega }](../_images/math/374e9373038412d5f4d74c0f5ae5f04601cce14f.png)
Die Spannung
![U= \unit[9]{V}](../_images/math/d51b6cce6cb884904bf0d19a3943aebdd2ab8d5c.png) bleibt an allen Stellen der
Parallelschaltung unverändert. Die Gesamt-Stromstärke
bleibt an allen Stellen der
Parallelschaltung unverändert. Die Gesamt-Stromstärke 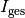 sowie die Stromstärken
sowie die Stromstärken 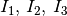 durch die Widerstände
durch die Widerstände
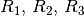 lassen sich mit Hilfe des Ohmschen Gesetzes
berechnen:
lassen sich mit Hilfe des Ohmschen Gesetzes
berechnen:![I_{\mathrm{ges}} = \frac{U}{R_{\mathrm{ges}}} &=
\frac{\unit[9]{V}}{\unit[76,2]{\Omega}} =~ \unit[0,12]{A} \\[6pt]
I_1 = \frac{U}{R_1} &= \frac{\unit[9]{V}}{\unit[100]{\Omega}} =~
\unit[0,09]{A} \\[4pt]
I_2 = \frac{U}{R_2} &= \frac{\unit[9]{V}}{\unit[470]{\Omega}} =~
\unit[0,02]{A} \\[4pt]
I_3 = \frac{U}{R_3} &= \frac{\unit[9]{V}}{\unit[1\,000]{\Omega}} =~
\unit[0,01]{A}](../_images/math/ed31bfb18cfb3910157f968b4ec3f0717b0f3d1a.png)
Bei einer Reihenschaltung lässt sich der Gesamtwiderstand
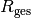 als Summe der einzelnen Widerstandswerte berechnen:
als Summe der einzelnen Widerstandswerte berechnen:![R_{\mathrm{ges}} = R_1 + R_2 + R_3 = \unit[100]{\Omega } +
\unit[470]{\Omega} + \unit[1\,000]{\Omega} = \unit[1\,570]{\Omega}](../_images/math/b4f18246f9ebde7092925a8d3464700136da1c77.png)
Durch Einsetzen der anliegenden Spannung
![U_{\mathrm{ges}} = \unit[9]{V}](../_images/math/b9e5cd20159ad9c1edd1ac66b4ba20df5fd58ab1.png) und des Gesamtwiderstands
und des Gesamtwiderstands ![R_{\mathrm{ges}} = \unit[1\,570]{\Omega}](../_images/math/d3e35bd0f37e7e584ba80d90ba5e5117f143d07d.png) in
das Ohmsche Gesetz folgt:
in
das Ohmsche Gesetz folgt: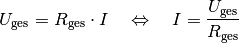
![I_{\mathrm{ges}} = \frac{U}{R_{\mathrm{ges}}} =
\frac{\unit[9]{V}}{\unit[1570]{\Omega}} \approx \unit[0,0057]{A} =
\unit[5,7]{mA}](../_images/math/458dfc526bddc1cfb14be39e19dd99b0c9178fc4.png)
Auch die an den einzelnen Widerständen anliegenden Spannungen lassen sich mit Hilfe des Ohmschen Gesetzes berechnen, wenn für die Stromstärke
![I = I_{\mathrm{ges}} \approx \unit[0,0057]{A}](../_images/math/f916c2844760f85655e141420032d6d181a597e4.png) eingesetzt wird:
eingesetzt wird:![U_1 &= R_1 \cdot I \approx \unit[100]{\Omega} \cdot
\unit[0,0057]{A} \approx \unit[0,6]{V} \\[4pt]
U_2 &= R_2 \cdot I \approx \unit[470]{\Omega} \cdot
\unit[0,0057]{A} = \unit[2,7]{V} \\[4pt]
U_3 &= R_3 \cdot I \approx \unit[1\,000]{\Omega} \cdot
\unit[0,0057]{A} = \unit[5,7]{V}](../_images/math/680d6537899ebfd71ca49a9e47ca62d47c881494.png)
Die Summe der drei Teilspannungen entspricht (von Rundungsfehlern abgesehen) wieder der Gesamtspannung
![(U_{\mathrm{ges}} = U_1 + U_2 + U_3 =
\unit[9]{V})](../_images/math/29e3068dac40f0eb8d6c36ff3d6bc6c1baeef1ca.png) .
.
Die Parallelschaltung der beiden Widerstände
![R_1 = \unit[470]{\Omega}](../_images/math/26eba7af3f3d79f8e6da3a57bab7e9e63c5c0d24.png) und
und ![R_2 = \unit[220]{\Omega}](../_images/math/754bdd90adbbb7e05c8969b2832f4393b562b6fa.png) wirkt nach außen wie ein einzelner
„Ersatzwiderstand“
wirkt nach außen wie ein einzelner
„Ersatzwiderstand“ 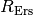 mit folgendem Wert:
mit folgendem Wert:![\frac{1}{R_{\mathrm{Ers}}} = \frac{1}{R_1 } + \frac{1}{R2} =
\unit[1]{\unit[470]{\Omega }} + \unit[1]{\unit[220]{\Omega}} \approx
\unit[0,0067]{\frac{1}{\Omega}}](../_images/math/aa4c69f4fc970c45ee13cb16fa4913fc37b63bec.png)
![\Rightarrow R_{\mathrm{Ers}} \approx \unit[150]{\Omega }](../_images/math/5f3bc0905b8e5f9d03410fce7f771fc48618db70.png)
Der gesamte Stromkreis kann damit als eine Reihenschaltung des Ersatzwiderstands
![R_{\mathrm{Ers}} \approx \unit[150]{\Omega}](../_images/math/6930dcdda06b8097bdc22b62c1824eda65c44187.png) und des Widerstands
und des Widerstands ![R_3 = \unit[560]{\Omega}](../_images/math/0a48ff941ee0ed7ffcb1051d4d5c40c81c6b79f7.png) aufgefasst
werden. Für den Gesamtwiderstand
aufgefasst
werden. Für den Gesamtwiderstand 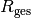 folgt:
folgt:![R_{\mathrm{ges}} = R_{\mathrm{Ers}} + R_3 \approx \unit[150]{\Omega } +
\unit[560]{\Omega} = \unit[710]{\Omega}](../_images/math/d1263d97a89d06ef982db1d73232e29caae57ee2.png)
Mit dem Ohmschen Gesetz lässt sich in Folge die Stromstärke
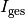 im unverzweigten Teil des Stromkreises
im unverzweigten Teil des Stromkreises ![(U_{\mathrm{ges}} =
\unit[9]{V},\, R_{\mathrm{ges}} \approx \unit[710]{\Omega})](../_images/math/411b86e4590116128bbe2ccecd0e5dabcf9b5a8f.png) bestimmen:
bestimmen: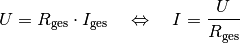
![I_{\mathrm{ges}} = \frac{U_{\mathrm{ges}}}{R_{\mathrm{ges}}} \approx
\frac{\unit[9]{V}}{\unit[710]{\Omega}} \approx \unit[0,013]{A} =
\unit[13]{mA}](../_images/math/2dd5b4e1f205f3110ea3c104950967d52899896d.png)
Mit
![I = I_{\mathrm{ges}} \approx \unit[0,013]{A}](../_images/math/8daa75c292d99e37326d034a03e60e13cce897a4.png) lassen sich die an
den Widerständen
lassen sich die an
den Widerständen 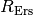 und
und 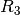 anliegenden
Spannungen
anliegenden
Spannungen 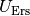 bzw.
bzw. 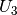 bestimmen:
bestimmen:![U_{\mathrm{Ers}} &= R_{\mathrm{Ers}} \cdot I \approx \unit[150]{\Omega} \cdot
\unit[0,013]{A} \approx \unit[1,9]{V} \\[6pt]
U_3 &= R_3 \cdot I \approx \unit[560]{\Omega} \cdot
\unit[0,013]{A} \approx \unit[7,1]{V}](../_images/math/9492383631a02e37bf10c30d97f3719983db8d80.png)
Die Spannung
![U_{\mathrm{Ers}} \approx \unit[1,9]{V}](../_images/math/e449b02eb6b99679dd7c421798c59ea145e121ae.png) liegt an beiden
parallelen Widerständen
liegt an beiden
parallelen Widerständen 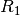 und
und 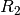 an. Für
die Stromstärken
an. Für
die Stromstärken 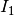 und
und 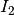 in diesen
beiden Stromzweigen ergibt sich somit:
in diesen
beiden Stromzweigen ergibt sich somit:![I_1 = \frac{U_{\mathrm{Ers}}}{R_1} \approx
\frac{\unit[1,9]{V}}{\unit[470]{\Omega}} \approx \unit[0,004]{A} \\[6pt]
I_1 = \frac{U_{\mathrm{Ers}}}{R_2} \approx
\frac{\unit[1,9]{V}}{\unit[220]{\Omega}} \approx \unit[0,009]{A}](../_images/math/fc9035776df4078f4181f010057795ef7276cb86.png)
Die Summe der beiden Stromstärken ist wiederum gleich der Stromstärke
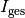 im unverzweigten Stromkreis.
im unverzweigten Stromkreis.
Anmerkungen:
| [1] | Durch eine Parallelschaltung mehrerer Batterien oder Akkus kann allerdings deren gespeicherte Energiemenge und damit die „Haltbarkeit“ der Stromquelle vergrößert werden. |
