Lösungen zur Linearen Algebra und analytischen Geometrie¶
Determinanten¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Determinanten.
Um die Determinante mittels der Regel von Sarrus zu bestimmen, schreibt man die erste und zweite Spalte noch einmal hinter die dritte Spalte. Dann berechnet man zunächst die Produkte der Zahlen in jeder Hauptdiagonalen (von links oben nach rechts unten) und bildet ihren Summenwert:
![& \begin{matrix}
1 & &3 & & \!\!\!\!-2 & & 1 & & 3\\
& \searrow & & \searrow & & \searrow \\
\!\!\!\!-1 & & \!\!\!\!-5 & & 4 & & \!\!\!\!-1 & & \!\!\!\!-5 \\
& & & \searrow & & \searrow & & \searrow \\
0 & & 7 & & \!\!\!\!-2 & & 0 & &7
\end{matrix} \\[6pt]
& = 10 + 0 + 14 = 24](../_images/math/0c8a37d1c099c7aa699e63743887a8d2ab91242f.png)
Anschließend bildet man die Summe der Produkte der in den Nebendiagonalen stehenden Zahlen (links unten nach rechts oben):
![& \begin{matrix}
1 & &3 & & \!\!\!\!-2 & & 1 & & 3\\
& & & \nearrow & & \nearrow & & \nearrow \\
\!\!\!\!-1 & & \!\!\!\!-5 & & 4 & & \!\!\!\!-1 & & \!\!\!\!-5 \\
& \nearrow & & \nearrow & & \nearrow \\
0 & & 7 & & \!\!\!\!-2 & & 0 & &7
\end{matrix} \\[6pt]
& = 0 + 28 + 6 = 34](../_images/math/db54fea7c87e92b42e96406593a3da63d7ae5093.png)
Schließlich subtrahiert man beide Werte voneinander; das Ergebnis lautet somit
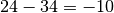 .
.
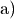 Zunächst kann man anhand der Koeffizienten-Determinate prüfen, ob das
Gleichungssystem eindeutig lösbar ist:
Zunächst kann man anhand der Koeffizienten-Determinate prüfen, ob das
Gleichungssystem eindeutig lösbar ist: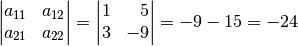
Der Wert der Determinante ist ungleich Null, das Gleichungssystem ist somit eindeutig lösbar.
Zur Bestimmung der Unbekannten
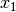 bildet man eine zweite
Determinante, wobei die Koeffizienten von
bildet man eine zweite
Determinante, wobei die Koeffizienten von 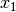 (die erste Spalte) durch
die Werte auf der rechten Gleichungsseite ersetzt werden:
(die erste Spalte) durch
die Werte auf der rechten Gleichungsseite ersetzt werden: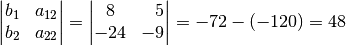
Dividiert man den Wert dieser Determinante durch den Wert der Koeffizienten-Determinate, so erhält man als Wert für
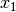 :
: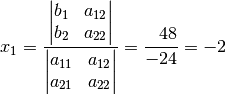
Zur Bestimmung der Unbekannten
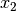 kann man entsprechend eine weitere
Determinante bilden, bei der nun die Koeffizienten von
kann man entsprechend eine weitere
Determinante bilden, bei der nun die Koeffizienten von 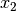 (die zweite
Spalte) durch die Werte auf der rechten Gleichungsseite ersetzt werden:
(die zweite
Spalte) durch die Werte auf der rechten Gleichungsseite ersetzt werden: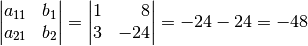
Dividiert man den Wert dieser Determinante durch den Wert der Koeffizienten-Determinate, so erhält man als Wert für
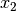 :
: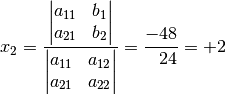
Das Gleichungssystem hat somit die Lösung
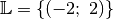 .
.
 Zunächst kann man wiederum anhand der
Koeffizienten-Determinate prüfen, ob das Gleichungssystem eindeutig lösbar
ist. Nach der Regel von Sarrus erhält man:
Zunächst kann man wiederum anhand der
Koeffizienten-Determinate prüfen, ob das Gleichungssystem eindeutig lösbar
ist. Nach der Regel von Sarrus erhält man: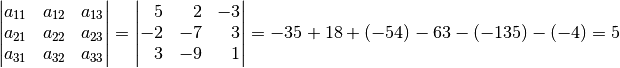
Der Wert der Determinante ist ungleich Null, das Gleichungssystem ist somit eindeutig lösbar.
Zur Bestimmung der Unbekannten
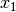 bildet man erneut eine
Determinante, wobei die Koeffizienten von
bildet man erneut eine
Determinante, wobei die Koeffizienten von 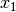 (die erste Spalte) durch
die Werte auf der rechten Gleichungsseite ersetzt werden:
(die erste Spalte) durch
die Werte auf der rechten Gleichungsseite ersetzt werden: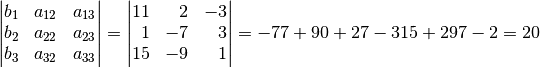
Dividiert man den Wert dieser Determinante durch den Wert der Koeffizienten-Determinate, so erhält man als Wert für
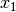 :
: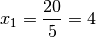
Zur Bestimmung der Unbekannten
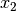 geht man wiederum von der
ursprünglichen Determinante aus, ersetzt allerdings die Koeffizienten von
geht man wiederum von der
ursprünglichen Determinante aus, ersetzt allerdings die Koeffizienten von
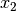 (die zweite Spalte) durch die Werte auf der rechten
Gleichungsseite:
(die zweite Spalte) durch die Werte auf der rechten
Gleichungsseite: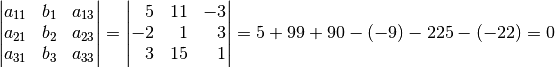
Der Wert dieser Determinante ist Null; somit ergibt auch eine Division durch den Wert
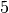 der Koeffizienten-Determinante den Wert
der Koeffizienten-Determinante den Wert 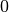 :
: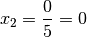
Zur Bestimmung der Unbekannten
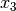 geht man erneut von der
ursprünglichen Determinante aus, ersetzt allerdings die Koeffizienten von
geht man erneut von der
ursprünglichen Determinante aus, ersetzt allerdings die Koeffizienten von
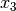 (die zweite Spalte) durch die Werte auf der rechten
Gleichungsseite:
(die zweite Spalte) durch die Werte auf der rechten
Gleichungsseite: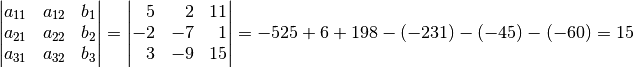
Dividiert man den Wert dieser Determinante durch den Wert der Koeffizienten-Determinate, so erhält man als Wert für
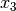 :
: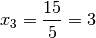
Das Gleichungssystem hat somit die Lösung
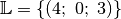 .
.
