Lösungen zur Wärmelehre¶
Temperatur und Wärme¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Temperatur und Wärme.
Um eine Temperatur von Grad Celsius in Grad Fahrenheit umzurechnen, muss man den Temperaturwert in die entsprechende Umrechnungsgleichung einsetzen:
![\text{Temperatur in \textdegree F} &= (\text{Temperatur in \textdegree
C} \cdot 1,8) + 32 \\[4pt]](../_images/math/2eb833b372185ba3aac1786a38492608b55d8f01.png)
Mit
![T_{\mathrm{C}} = \unit[20]{\degree C }](../_images/math/096d33352f97dc9f8a2bb6184c7be23157dd8f75.png) gilt somit:
gilt somit:![T_{\mathrm{F}} = (T_{\mathrm{C}} \cdot 1,8) + 32 = \unit[((20 \cdot 1,8) +
32)]{\degree F} = \unit[68]{\degree F}](../_images/math/aff12d2982a97aa5497659b27d1426c91add3660.png)
Eine Temperatur von
![\unit[20]{\degree C }](../_images/math/7f8eee4581c2aeafbdf974efe4cdfb5386b449bc.png) entspricht somit einer
Temperatur von
entspricht somit einer
Temperatur von ![\unit[68]{\degree F}](../_images/math/3e2926e25f39912bc2b4f125e0d114fb63c51be5.png) .
.
Um eine in Grad Celsius angegebene Temperatur in Kelvin umzurechnen, muss lediglich
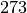 zum Temperaturwert hinzu addiert werden:
zum Temperaturwert hinzu addiert werden:![\text{Temperatur in K} &= \text{Temperatur in \textdegree C} + 273
\\[4pt]](../_images/math/5c9cd637147afe159578270a42c890ea1269a820.png)
Mit
![T_{\mathrm{C}} = \unit[40]{\degree C }](../_images/math/963bf8155a7185989820c8051c9dd7fd91446b48.png) folgt somit:
folgt somit:![T = T_{\mathrm{C}} + 273 = \unit[40 + 273]{K} = \unit[313]{K}](../_images/math/5ec5c8b3663e0ae80ddb78eb378d4847ecf36fe0.png)
Zur Umrechnung von Grad Celsius in Grad Fahrenheit muss der gegebene Temperaturwert in die passende Umrechnungs-Gleichung eingesetzt werden:
![\text{Temperatur in \textdegree F} &= (\text{Temperatur in \textdegree
C} \cdot 1,8) + 32 \\[4pt]](../_images/math/2eb833b372185ba3aac1786a38492608b55d8f01.png)
Eingesetzt ergibt sich:
![T_{\mathrm{F}} = (T_{\mathrm{C}} \cdot 1,8) + 32 = \unit[((40 \cdot 1,8) +
32)]{\degree F} = \unit[104]{\degree F}](../_images/math/3f92c8d45b9c60ac5c1ccbcade5d6cbcc87f3939.png)
Eine Temperatur von
![\unit[40]{\degree C }](../_images/math/f9f9e17747bf61c4e7be83f10610ef20619e45b5.png) entspricht somit einer
Temperatur von
entspricht somit einer
Temperatur von ![\unit[313]{K}](../_images/math/828c7e7bba0c74e06fc0cda6ca741b577de48462.png) bzw. von
bzw. von ![\unit[68]{\degree F}](../_images/math/3e2926e25f39912bc2b4f125e0d114fb63c51be5.png) .
.
Wärmekapazität und Phasenübergänge¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Wärmekapazität und Phasenübergänge.
Um
![m=\unit[5]{kg}](../_images/math/b56202c4a99d73bb2a5100908738b7d73c2acf9c.png) Eis mit einer Schmelzwärme von
Eis mit einer Schmelzwärme von ![q_{\mathrm{s}} =
\unit[334]{kJ/kg}](../_images/math/13ae2e3d63d75a412948580a817af31683793086.png) und einer Temperatur von
und einer Temperatur von ![T = \unit[0]{\degree C}](../_images/math/41d1613be30a3ba5847fcf9d83ce0447425058f3.png) zu
schmelzen, muss eine Wärmemenge
zu
schmelzen, muss eine Wärmemenge 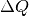 zugeführt werden, die der
Schmelzwärme dieser Eismenge entspricht:
zugeführt werden, die der
Schmelzwärme dieser Eismenge entspricht:![Q = m \cdot q_{\mathrm{s}} = \unit[5]{kg} \cdot \unit[334]{\frac{kJ}{kg}} =
\unit[1670]{kJ}](../_images/math/1cfba743f76486e43db33fb031be2c99d2bc3b60.png)
Mit dieser Wärmemenge würden sich
![m=\unit[5]{kg}](../_images/math/b56202c4a99d73bb2a5100908738b7d73c2acf9c.png) Wasser mit einer
spezifischen Wärmemenge von
Wasser mit einer
spezifischen Wärmemenge von ![c=\unit[4,2]{\frac{kJ}{kg \cdot K}}](../_images/math/15cabccffc0087175e51c8dfcf13f796e9dd6f24.png) und
einer Temperatur von
und
einer Temperatur von ![T_1 = \unit[0]{\degree C}](../_images/math/11640d5d2437f8cb33aad9c3718c6bf765182ffc.png) um folgende
Temperaturdifferenz
um folgende
Temperaturdifferenz  erwärmen:
erwärmen:![Q = m \cdot c \cdot \Delta T \quad \Longleftrightarrow \quad \Delta T =
\frac{Q}{m \cdot c} = \frac{\unit[1670]{kJ}}{\unit[5]{kg} \cdot
\unit[4,2]{\frac{kJ}{kg \cdot K}}} \approx \unit[79,5]{\degree C}](../_images/math/16d0d73ef4bd4038423fe62d0b28375c8eb0b059.png)
Mit der zum Schmelzen von Eis nötigen Wärmemenge könnte die gleiche Masse an Wasser somit auf knapp
![\unit[80]{\degree C}](../_images/math/4ede412709dca0ea0c217910ffe72b1582073727.png) erhitzt werden.
erhitzt werden.
Für die zum Erwärmen nötige Energiemenge für
![m = \rho \cdot V =
\unit[1,0]{\frac{kg}{dm^3}} \cdot \unit[3,0]{dm^3} = \unit[3,0]{kg}](../_images/math/d81f049cacb68d37e66cc100dfe53e454cee6f2d.png) Wasser
gilt:
Wasser
gilt:![\Delta Q = m \cdot c \cdot \Delta T = \unit[3,0]{kg} \cdot
\unit[4,2]{\frac{kJ}{kg \cdot K}} \cdot \unit[80]{K} \approx \unit[1008]{kJ}](../_images/math/e2ff8b540af26a36fda5b3615bdeb767b1334cc9.png)
Beträgt die Heizleistung
![P=\unit[2,0 \cdot 10^3]{W}](../_images/math/66588bb2dba6810fbca6a46fac19bd9be84fdc2b.png) , so ist folgende
Zeit für das Erwärmen nötig:
, so ist folgende
Zeit für das Erwärmen nötig:![P = \frac{\Delta E}{\Delta t} \quad \Longleftrightarrow \quad \Delta t =
\frac{\Delta E}{P} = \frac{\unit[1008 \cdot 10^{3}]{J}}{\unit[2,0 \cdot 10^3]{W}}
\approx \unit[504]{s} \approx \unit[8,4]{min}](../_images/math/5b3d03b1c5d80a9524e1ba23ba87c72ffc6e57a9.png)
Zur Erwärmung sind somit (von Wärmeverlusten abgesehen) rund
![\unit[8,4]{min}](../_images/math/4bdfdeef9e5bf799912e4d740071a6084a68730f.png) nötig.
nötig.
Ausbreitung von Wärme¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Ausbreitung von Wärme.
Der Wärmestrom
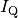 durch das einfach verglaste Fenster kann
direkt mit Hilfe der Wärmeleitungs-Formel berechnet werden. Mit
durch das einfach verglaste Fenster kann
direkt mit Hilfe der Wärmeleitungs-Formel berechnet werden. Mit ![A =
\unit[2]{m^2}](../_images/math/756a1adfe6a910a41f0ff708dec98c1d357ce81b.png) ,
, ![\lambda = \unit[1]{\frac{W}{m \cdot K}}](../_images/math/b7a7958a7087b07a77b4a4dae021b283a5ecb7bb.png) ,
, ![l =
\unit[4]{mm}](../_images/math/328a6bfdb140db5ee174cc9a23462705aeacffde.png) und
und ![\Delta T = \unit[20]{\degree C} -
\unit[5]{\degree C}= \unit[15]{K}](../_images/math/d573b181e21258c40ae5160f830c7d7e99ae49a3.png) folgt:
folgt:![I_{\mathrm{Q}} &= j_{\mathrm{Q}} \cdot A = \frac{\lambda \cdot A}{l} \cdot
\Delta T \\ &= \frac{\unit[1]{\frac{W}{m \cdot K}} \cdot \unit[1,0]{m^2}}{\unit[0,004]{m}} \cdot
\unit[15]{K} = \unit[3\,750]{W}](../_images/math/8fa7a946bf5dcbd6703814b4c883396d7c964d3d.png)
Der Wärmestrom ist mit
![\unit[3\,750]{Watt}](../_images/math/82e1f1470085d29692a44c3be244f0d296f34540.png) sehr hoch. Man würde eine
ebenso hohe Heizleistung benötigen, um den Wärmeverlust zu kompensieren,
andernfalls würde die Temperatur im Zimmer absinken.
sehr hoch. Man würde eine
ebenso hohe Heizleistung benötigen, um den Wärmeverlust zu kompensieren,
andernfalls würde die Temperatur im Zimmer absinken.
Bei einem Wärmestrom durch ein doppelt verglastes Fenster sind die einzelnen Wärmewiderstände in Reihe geschaltet; es addieren sich somit die einzelnen Wärmewiderstände. Alle Widerstände haben die gleiche Querschnittsfläche
![A_1 = A_2 = A3 = \unit[2]{m^2}](../_images/math/a8b7ab8c431400dd2de4724b01e44020e52e16f7.png) , zudem sind die Schichtdicken
, zudem sind die Schichtdicken
![l_1 = l_3 = \unit[4]{mm}](../_images/math/2bc3eb21b3532befa65d779e996f1a768809f3bd.png) sowie die Wärmeleitfähigkeiten
sowie die Wärmeleitfähigkeiten
![\lambda_1 = \lambda_3 = \unit[1]{\frac{W}{m \cdot K}}](../_images/math/5c0ac91b3fb55bc343e011fc01809b27d8839d38.png) der beiden
Glassscheiben identisch. Mit der Schichtdicke
der beiden
Glassscheiben identisch. Mit der Schichtdicke ![l_2 = \unit[1]{cm}](../_images/math/d077c17359e8c745c20e3359691ea17e8398b277.png) des
Luftspalts und dessen Wärmeleitfähigkeit
des
Luftspalts und dessen Wärmeleitfähigkeit ![\lambda_2 =
\unit[0,025]{\frac{W}{m \cdot K}}](../_images/math/991b0581d00ce6c8d07f4ee0df707e6fd3162b4b.png) folgt für den Gesamtwiderstand:
folgt für den Gesamtwiderstand:![R_{\mathrm{ges}} &= R_1 + R_2 + R_3 = 2 \cdot R_1 + R_2 \\ &= 2 \cdot
\left( \frac{l_1}{\lambda_1 \cdot A_1}\right) + \frac{l_2}{\lambda_2 \cdot
A_2} \\
&= 2 \cdot \left( \frac{\unit[0,004]{m}}{\unit[1]{\frac{W}{m \cdot K}}
\cdot \unit[2]{m^2}}\right) +\frac{\unit[0,01]{m}}{\unit[0,025]{\frac{W}{m
\cdot K}} \cdot \unit[2]{m^2}} = \unit[0,204]{\frac{K}{W}}](../_images/math/8328a0236a51f8de196021291b20573716ece266.png)
Für den Wärmestrom gilt damit:
![I_{\mathrm{Q,RS}} = \frac{\Delta T}{R_{\mathrm{ges}}} =
\frac{\unit[15]{K}}{\unit[0,204]{\frac{K}{W}}} \approx \unit[73,5]{W}](../_images/math/2cc6081e2cfe9181244112ef47642ec5eb1bbfb9.png)
Obwohl das Fenster eine doppelt so große Fläche
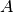 hat wie das einfach
verglaste Fenster im letzten Beispiel, ist der Wärmestrom in diesem Fall
erheblich geringer. Aus diesem Grund werden inzwischen fast nur noch doppelt
(oder sogar dreifach) verglaste Fenster in Häuser eingebaut.
hat wie das einfach
verglaste Fenster im letzten Beispiel, ist der Wärmestrom in diesem Fall
erheblich geringer. Aus diesem Grund werden inzwischen fast nur noch doppelt
(oder sogar dreifach) verglaste Fenster in Häuser eingebaut.
Bei einer Verdopplung der Temperatur ergibt sich folgendes Verhältnis der Strahlungsleistungen:
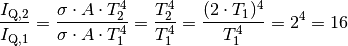
Bei einer Verdopplung der Temperatur steigt die Strahlungsleistung somit um das
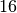 -fache an.
-fache an.Erhöht man die Temperatur eines Wärmestrahlers von
![T_1 =
\unit[10]{\degree C}](../_images/math/e2914534a0f9f65f7483d52aced10cfb764745b9.png) auf
auf ![T_2 = \unit[40]{\degree C}](../_images/math/c3b80d5897c9327bf6cf024140185df97c05a039.png) , so folgt für
das Verhältnis der Strahlungsleistungen:
, so folgt für
das Verhältnis der Strahlungsleistungen:![\frac{I_{\mathrm{Q,2}}}{I_{\mathrm{Q,1}}} = \frac{\sigma \cdot A \cdot
T_2^4}{\sigma \cdot A \cdot T_1^4} = \frac{T_2^4}{T_1^4} =
\frac{(\unit[(273+40)]{K})^4}{(\unit[(273+10)]{K})^4} \approx 1,5](../_images/math/d6aacdc574e73ac5f28f4e79764221bdc268c18d.png)
Bei einer Erhöhung von
![\unit[10]{\degree C}](../_images/math/4a31ca78b8545be3309cc8a125648306158e1d61.png) auf
auf
![\unit[40]{\degree }](../_images/math/c7bae175e0012258945680a655fdc8d4c0361080.png) steigt die Strahlungsleistung auf das
steigt die Strahlungsleistung auf das
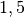 -fache, also um
-fache, also um 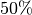 an. Entscheidend ist hierbei, dass mit
absoluten Temperaturwerten gerechnet wird und eine vierfache
Celsius-Temperatur somit nicht einer vierfachen Kelvin-Temperatur entspricht.
an. Entscheidend ist hierbei, dass mit
absoluten Temperaturwerten gerechnet wird und eine vierfache
Celsius-Temperatur somit nicht einer vierfachen Kelvin-Temperatur entspricht.
Ausdehnung bei Erwärmung¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Ausdehnung bei Erwärmung.
Durch die Erwärmung dehnt sich das Metall-Lineal und damit auch seine Mess-Skala leicht aus. Mit dem erhitzten Lineal gemessene Werte sind somit aufgrund der gestreckten Skala geringfügig zu klein.
Beispiel:
Angenommen, das Lineal bestünde aus Eisen; damit würde es sich um
![\alpha_{\mathrm{Fe}} = \unit[0,0121]{mm}](../_images/math/db2ace3d8a10b0abf6d5624a987d359c4b64f062.png) je Meter Ausgangslänge und je
Kelvin Temperaturerhöhung ausdehnen. Ist das Lineal beispielsweise
je Meter Ausgangslänge und je
Kelvin Temperaturerhöhung ausdehnen. Ist das Lineal beispielsweise ![l
= \unit[50]{cm} = \unit[0,5]{m}](../_images/math/bbe9610ae403fb5399e51e089b3a00ca1d3edfd7.png) lang und heizt sich um
lang und heizt sich um ![\Delta T =
\unit[50]{K}](../_images/math/078f7e4fb79b4dc8196afcc92d070d4d88f2c456.png) auf, so dehnt es sich um folgende Länge aus:
auf, so dehnt es sich um folgende Länge aus:![\Delta l = \alpha \cdot l \cdot \Delta T = \unit[0,0121]{\frac{mm}{m
\cdot K} } \cdot \unit[0,5]{m} \cdot \unit[50]{K} = \unit[0,30]{mm}](../_images/math/b731d6346bf556010e45d058c649d37a203b26a5.png)
Das Lineal dehnt sich in diesem Beispiel somit trotz heftiger Erwärmung um nur
![\unit[0,3]{mm}](../_images/math/5d46bf42053079ff46953aee30f0936ab5f22514.png) weit aus. Da Messwerte niemals
weit aus. Da Messwerte niemals 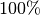 -ig
korrekt abgelesen werden können, ist die Ausdehnung durch Erwärmung in
diesem Fall nicht von Bedeutung. Auch das erhitzte Lineal kann somit weiter
zur Längenmessung verwendet werden.
-ig
korrekt abgelesen werden können, ist die Ausdehnung durch Erwärmung in
diesem Fall nicht von Bedeutung. Auch das erhitzte Lineal kann somit weiter
zur Längenmessung verwendet werden.
Aluminium hat den größeren Längen-Ausdehnungskoeffizient als Stahl
![(\unit[0,024]{\frac{mm}{m \cdot K} } > \unit[0,010]{\frac{mm}{m
\cdot K} })](../_images/math/56c32f884ea4ea11bf6ac18c15b760cde6338a8c.png) ; es dehnt sich somit bei Erwärmung stärker aus als Stahl. Soll
sich der Bimetall-Streifen nach oben verbiegen, muss somit sich das Aluminium
unten beziehungsweise der Chrom-Stahl oben befinden.
; es dehnt sich somit bei Erwärmung stärker aus als Stahl. Soll
sich der Bimetall-Streifen nach oben verbiegen, muss somit sich das Aluminium
unten beziehungsweise der Chrom-Stahl oben befinden.
Der Längen-Ausdehnungskoeffizient von Kupfer beträgt
![(\alpha
_{\mathrm{Cu}} = \unit[0,0168]{\frac{mm}{m \cdot K} })](../_images/math/e46832ce1ad03f433f6b01160d04c7bc6c34cbc1.png) . Durch die Erwärmung um
. Durch die Erwärmung um
![\Delta T = \unit[50]{K}](../_images/math/75cf2cbf3a7529550dfcd381bcbb971394acea4a.png) dehnt sich der
dehnt sich der ![\unit[120]{m}](../_images/math/710027aaa2f9afd55ef2f78ab38a51529e0e3ea0.png) lange
Draht somit um folgenden Betrag aus:
lange
Draht somit um folgenden Betrag aus:![\Delta l = \alpha \cdot l \cdot \Delta t = \unit[0,0168]{\frac{mm}{m
\cdot K} } \cdot \unit[120]{m} \cdot \unit[50]{K} = \unit[100,8]{mm} =
\unit[10,08]{cm}](../_images/math/45e345ad4e76dedd491e6b9d2669ea44b5e28769.png)
Der Kupfer-Draht dehnt sich somit um rund
![\unit[10]{cm}](../_images/math/b701ff2810b220d0bf62d25e7472401474b6e0ff.png) aus. Seine
neue Länge beträgt damit
aus. Seine
neue Länge beträgt damit ![l + \Delta l \approx \unit[120,1]{m}](../_images/math/3b6b05a92f5b28b3fd9587baac860696fcf489a2.png) .
.
Die Längenschwankung Brücke kann anhand der Temperaturunterschiede
![(T_2
-T_1 = \unit[(-15 - 15)]{K} = \unit[-30]{K}](../_images/math/c495af19459c72a032b9cf2387e83e222afc9ae9.png) im Winter beziehungsweise
im Winter beziehungsweise
![(T_3 - T_1 = \unit[(+40 - 15)]{K} = \unit[+25]{K}](../_images/math/50f08ab95f7d1be4ed0e6acf89375c2acc4b21b2.png) im Sommer
berechnet werden:
im Sommer
berechnet werden:![l_2 &= l_1 \cdot (1 + \alpha \cdot (T_2-T_1) = \unit[300]{m} \cdot (1 +
\unit[12 \cdot 10^{-6}]{\frac{1}{K}} \cdot \unit[(-30)]{K}) \approx
\unit[299,892]{m} \\[4pt]
l_3 &= l_1 \cdot (1 + \alpha \cdot (T_3-T_1) = \unit[300]{m} \cdot (1 +
\unit[12 \cdot 10^{-6}]{\frac{1}{K}} \cdot \unit[(+25)]{K}) \approx
\unit[300,09]{m} \\[4pt]](../_images/math/229dac254dc39bccc37a98a0caf01a5575715966.png)
Die Längenschwankung der Brücke zwischen sommererlichen und winterlichen Temperaturen beträgt somit
![l_3 - l_2 \approx \unit[19,8]{cm}](../_images/math/0c17b2fb0821e1126e022ee6795618ca33d98c52.png)
Für den Stahltank als Festkörper gilt
![\gamma \approx 3 \cdot \alpha =
\unit[35,4 \cdot 10^{-6}]{\frac{1}{K}}](../_images/math/db2db07a5b8611a9bd86a1bc335aed49aa1c6594.png) . Damit dehnt sich der Tank bei der
Temperaturerhöhung um
. Damit dehnt sich der Tank bei der
Temperaturerhöhung um ![\Delta T = \unit[35]{K}](../_images/math/b57d0ea1a2c050bf7df71fe882cef9ca6e259951.png) auf folgendes Volumen
aus:
auf folgendes Volumen
aus:![V_{\mathrm{neu}} = V_0 \cdot (1 + \gamma_{\mathrm{Stahl}} \cdot \Delta T)
= \unit[50]{l} \cdot (1 + \unit[35,4 \cdot 10^{-6}]{\frac{1}{K}} \cdot
\unit[35]{K} \approx \unit[50,06]{l}](../_images/math/d5d1777c68176e1cc25bc34b46caec120919cd84.png)
Ein ebenso großes Ausgangsvolumen an Benzin dehnt sich hingegen bei gleicher Temperaturdifferenz auf folgendes Volumen aus:
![V_{\mathrm{neu}} = V_0 \cdot (1 + \gamma_{\mathrm{Benzin}} \cdot \Delta T)
= \unit[50]{l} \cdot (1 + \unit[1,06 \cdot 10^{-3}]{\frac{1}{K}} \cdot
\unit[35]{K} \approx \unit[51,86]{l}](../_images/math/37b9c4d100a87e4ea614187a91144824da71bc6a.png)
Das Benzin dehnt sich folglich wesentlich stärker aus als der Tank. Bei einem randvoll gefüllten Tank besteht somit die Gefahr, dass er sich bei Erwärmung verformt oder reißt; Tankbehälter sollten somit nie komplett gefüllt werden, oder ersatzweise (beispielsweise bei Heizungsanlagen) mit einem Überlauf-Gefäß ausgestattet sein.
Eine Besonderheit („Anomalie“) des Wassers liegt darin, dass es sich beim Erwärmen von
![\unit[0]{\degree C }](../_images/math/e5d0d91bddea192b9039d5bf324be1816553890b.png) bis zu einer Temperatur von
bis zu einer Temperatur von
![\unit[4]{\degree C}](../_images/math/eed4ef41d7331125df384be9e18fd591c56a1acf.png) zunächst zusammenzieht; erst ab einer höheren
Temperatur
zunächst zusammenzieht; erst ab einer höheren
Temperatur ![T > \unit[4]{\degree C}](../_images/math/b63b51f8ea63425cdfadcb791f0802c64de7991e.png) dehnt es sich wieder aus. Wasser hat
somit bei
dehnt es sich wieder aus. Wasser hat
somit bei ![\unit[4]{\degree C }](../_images/math/048c9ce4b16235a92b57cd2e2399948832f85dfc.png) seine höchste Dichte.
seine höchste Dichte.Eine zweite Besonderheit des Wassers liegt darin, dass es sich beim Erstarren nicht zusammenzieht, sondern etwa um
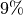 seines Volumens
ausdehnt. Eis hat somit eine geringere Dichte als Wasser und kann daher auf
Wasser schwimmen.
seines Volumens
ausdehnt. Eis hat somit eine geringere Dichte als Wasser und kann daher auf
Wasser schwimmen.
Jedes Gas füllt stets den ganzen Raum aus, der ihm zur Verfügung gestellt wird. Möchte man ein Gasvolumen komprimieren, so muss gegen das Gas Arbeit verrichtet werden. Diese Arbeit wird im Gas in Form von innerer Energie gespeichert: Es erhöht sich damit (theoretisch) der Druck oder die Temperatur des Gases oder (in der Praxis) beide Größen zusammen.
Beim Zusammendrücken einer Luftpumpe erwärmt sich diese zum einen aufgrund der Reibung des Kolbens am Gehäuse der Luftpumpe, zum anderen wird stets ein Teil der zugeführten Kompressionsarbeit in Wärme-Energie umgewandelt.[1]
Nach dem Modell eines idealen Gases kann das Eigenvolumen der Gasteilchen gegenüber dem Volumen, das diese anhand ihrer Bewegung einnehmen, völlig vernachlässigt werden (die Teilchen selbst haben quasi kein Eigenvolumen).
Wird ein (ideales) Gas abgekühlt, so nimmt die Geschwindigkeit der Gasteilchen ab. Da sie damit weniger Platz beanspruchen, sinkt dementsprechend auch der Gasdruck (bei gleich bleibendem Volumen) bzw. das Volumen (bei gleich bleibendem Druck).[2] Bei einer Abkühlung hin zum absoluten Temperatur-Nullpunkt
![(\unit[-273]{K} \text{ bzw. }
\unit[0]{K})](../_images/math/47143b52b22282132d6b223bff9573a26fd3981b.png) würde die Eigenbewegung der Gasteilchen zum Stillstand kommen
und sich somit auch das Volumen des idealen Gases auf null reduzieren.
würde die Eigenbewegung der Gasteilchen zum Stillstand kommen
und sich somit auch das Volumen des idealen Gases auf null reduzieren.Die Teilchen realer Gase haben ein endliches Eigenvolumen, zudem wirken (sehr schwache) Kräfte zwischen den einzelnen Gasteilchen. Reale Gase kondensieren deshalb, bevor sie den absoluten Temperatur-Nullpunkt erreichen.[3]
Nach der Zustandsgleichung eines idealen Gases ist der Quotient
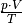 eines bestimmten Gasvolumens stets konstant.
Das gesuchte Volumen
eines bestimmten Gasvolumens stets konstant.
Das gesuchte Volumen 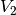 nach der angegebenen
Zustandsänderung kann durch Auflösung der Zustandsgleichung aus den
übrigen fünf Größen berechnet werden:
nach der angegebenen
Zustandsänderung kann durch Auflösung der Zustandsgleichung aus den
übrigen fünf Größen berechnet werden:
Setzt man die gegebenen Werte ein
![(p_1 = \unit[1]{bar},\; T_1 =
\unit[300]{K},\; V_1 = \unit[30]{cm^3},\; p_2 = \unit[4]{bar},\; T_2 =
\unit[500]{K})](../_images/math/98493de06b108b3d7661ed455d709c7ffe0214f2.png) , so erhält man:
, so erhält man:![V_2 = \frac{p_1 \cdot V_1 \cdot T_2 }{T _1 \cdot p_2 } =
\frac{\unit[1]{bar} \cdot \unit[30]{cm^3} \cdot
\unit[500]{K}}{\unit[300]{K} \cdot \unit[4]{bar}} = \unit[12,5]{cm^3}](../_images/math/bd9984ae06870c8ef0c259c289bab719bac944fd.png)
Das neue Volumen beträgt somit
![\unit[12,5]{cm^3}](../_images/math/05b0d2305c7e9df1d06eef26425cd7d0650a55d2.png) .
.
Bleibt der Druck
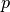 während der Zustandsänderung eines Gases
konstant, vereinfacht sich die Zustandsgleichung für ideale Gase
folgendermaßen:
während der Zustandsänderung eines Gases
konstant, vereinfacht sich die Zustandsgleichung für ideale Gase
folgendermaßen: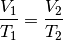
Somit kann durch Einsetzen der gegebenen Größen
![(V_1 =
\unit[20]{m^2} \times \unit[2,5]{m} = \unit[50]{m^3},\, T_1 =
\unit[12]{\degree C } = \unit[285]{K} ,\, T_2 = \unit[20]{\degree C} =
\unit[293]{K})](../_images/math/2cc4015d5da577cebac76e71070f19b14c7fba87.png) das Volumen der erwärmten Luft
das Volumen der erwärmten Luft 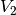 berechnet
werden:
berechnet
werden: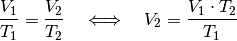
![V_2 = \frac{V_1 \cdot T_2}{T_1} = \frac{\unit[50]{m^3} \cdot
\unit[293]{K}}{\unit[285]{K}} \approx \unit[51,4]{m^3}](../_images/math/299c05714d1894c52b9d69a4841d1e9cf36f73e0.png)
Bei gleichem Druck würde sich die Luft somit auf ein Volumen von
![\unit[51,4]{m^3}](../_images/math/d9b594eab7773838384aec3c633e0c9db0576339.png) ausdehnen. Da das Volumen des Raum jedoch nur
ausdehnen. Da das Volumen des Raum jedoch nur
![\unit[50]{m^3}](../_images/math/5e65e2e6c9ccaaa1af4a693bdf1f1e14ab808fac.png) beträgt, müssen bei der höheren Temperatur
beträgt, müssen bei der höheren Temperatur
![\Delta V = V_2 - V_1 = \unit[1,4]{m^3}](../_images/math/a4fa89915856699edf42f3887772fcbeb2237f4d.png) Luft aus dem Raum entweichen.
Luft aus dem Raum entweichen.
Der Behälter enthält
![V_1=\unit[500]{l}](../_images/math/cfaee65d4b634d69c76ad76abce110feaf1cadd0.png) Luft bei einem Überdruck von
Luft bei einem Überdruck von
![\unit[3 \cdot 10^5]{Pa}](../_images/math/4f1e9b1a59443bd6e1b5f825fb83fd4b9377437f.png) , der absolute Luftdruck im Behälter beträgt
somit
, der absolute Luftdruck im Behälter beträgt
somit ![\unit[4 \cdot 10^5]{Pa}](../_images/math/1091f71d12a2011946c6348e34bf8b4d6d31ea0a.png) . Als Ergebnis sollen
. Als Ergebnis sollen
![V_2=\unit[500]{l}](../_images/math/2df0ac6d120da704a61becf418f29ad667878154.png) bei einem Überdruck von
bei einem Überdruck von ![\unit[8 \cdot
10^5]{Pa}](../_images/math/d9b31ee3fa10b1758723ed8995a124e9c4b645d0.png) , also einem absoluten Druck von
, also einem absoluten Druck von ![p_2 = \unit[9 \cdot
10^5]{Pa}](../_images/math/78f56f3c2bfe5f6cdcb00c3b928aa6324964a329.png) vorliegen. Dafür müsste bei dem anfänglichen Druck
vorliegen. Dafür müsste bei dem anfänglichen Druck
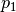 folgendes Volumen
folgendes Volumen 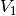 vorliegen:
vorliegen:![p_1 \cdot V_1 = p_2 \cdot V_2 \quad \Longleftrightarrow \quad V_1 =
\frac{p_2}{p_1}\cdot V_2 \\[5pt]
V_1 = \frac{\unit[9 \cdot 10^5]{Pa}}{\unit[4 \cdot 10^5]{Pa}} \cdot
\unit[500]{l} = \unit[1125]{l}](../_images/math/bb602d7529ccbca3080fffcd02c6fa314becf7fb.png)
Tatsächlich sind allerdings nur
![\unit[500]{l}](../_images/math/a100690f6d9b08424c28a4a4bb8239a38023732e.png) bei diesem Druck im
Behälter enthalten. Es müssen also
bei diesem Druck im
Behälter enthalten. Es müssen also ![V_1^{*} = \unit[625]{l}](../_images/math/4b1eb6cc1dc6d3807f1ce3d853198f0f34794d10.png) zusätzlich bei einem Druck von
zusätzlich bei einem Druck von 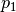 im Behälter enthalten sein. Dazu
ist folgende Luftmenge bei Normaldruck
im Behälter enthalten sein. Dazu
ist folgende Luftmenge bei Normaldruck 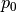 nötig:
nötig:![p_0 \cdot V_0 = p_1 \cdot V_1 ^{*} \quad \Longleftrightarrow \quad V_0 =
\frac{p_1}{p_0} \cdot V_1 ^{*} \\[5pt]
V_0 = \frac{\unit[4 \cdot 10^5]{Pa}}{\unit[1 \cdot 10^5]{Pa}} \cdot
\unit[625]{l} = \unit[2500]{l}](../_images/math/fe403728810a32465f35993077f1ca1f72ea1731.png)
Es ist somit eine zusätzliche Luftmenge von
![\unit[2500]{l}](../_images/math/844c4bdc7511ccbc546fec36d69dde0a0ed95d6e.png) bei
Normaldruck nötig.
bei
Normaldruck nötig.
Allgemeine Gasgleichung¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Allgemeine Gasgleichung.
Nach der allgemeinen Gasgleichung gilt:
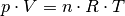
Unter Normalbedingungen gilt für den Druck
![p=\unit[1,0 \cdot
10^{5}]{Pa}](../_images/math/5cd5fe5108cca9c79a334ee0a79c070b8a5b15db.png) und für die Temperatur
und für die Temperatur ![T=\unit[0]{\degree C} =
\unit[273,15]{K}](../_images/math/95b48721e771aceef6189b2a8ef79eaf347bf937.png) . Somit ergibt sich für die im Volumen
. Somit ergibt sich für die im Volumen
![V=\unit[1,0]{l}](../_images/math/9156f9dced6787ec25d065ba99ee4f261a76da22.png) enthaltene Luft folgende Stoffmenge
enthaltene Luft folgende Stoffmenge 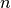 :
:![n = \frac{p \cdot V}{R \cdot T} = \frac{\unit[1,0 \cdot 10^{5}]{Pa} \cdot
\unit[1,0 \cdot 10^{-3}]{m^3}}{\unit[8,31]{\frac{J}{mol \cdot K}} \cdot
\unit[273,15]{K}} \approx \unit[0,044]{mol}](../_images/math/7d8abf3764cdb7db975a3b2f795770a254c822af.png)
Die Einheit ergibt sich, wenn man
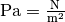 und
und
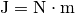 setzt:
setzt: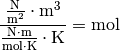
Für die Anzahl
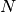 an Teilchen ergibt sich aufgrund der Beziehung
an Teilchen ergibt sich aufgrund der Beziehung
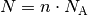 :
:![N = n \cdot N_{\mathrm{A}} = \unit[0,044]{mol} \cdot \unit[6,022 \cdot
10^{23}]{\frac{1}{mol}} \approx 2,7 \cdot 10^{22}](../_images/math/2b25fdf21e81508f210941735185e0da30bf2b35.png)
In einem Luft sind somit rund
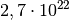 Teilchen enthalten.
Teilchen enthalten.
Nach der allgemeinen Gasgleichung gilt:
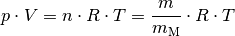
Diese Gleichung kann nach
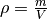 aufgelöst werden:
aufgelöst werden: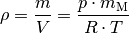
Die molare Masse für Luft beträgt
![m_{\mathrm{M}} \approx
\unit[29]{\frac{g}{mol}}](../_images/math/d90fb60a691cb8208c868c5d52fe405c7ea8fc02.png) . Mit
. Mit ![T = \unit[(273+20)]{K}](../_images/math/9e2faf0c396149bfa0379ed8ead80203eac9797a.png) und
und ![p =
\unit[1 \cdot 10 ^{-10}]{Pa}](../_images/math/202c263a53dc0f5771b385ed314b6e784192150a.png) folgt:
folgt:![\rho = \frac{\unit[1 \cdot 10 ^{-10}]{Pa} \cdot
\unit[29]{\frac{g}{mol}}}{\unit[8,31]{\frac{J}{mol \cdot K}} \cdot
\unit[(273+20)]{K}} \approx \unit[1,19 \cdot 10 ^{-12}]{\frac{g}{m^3}}](../_images/math/2c57fbfad398fa661b8fc76273d69297d3028ec6.png)
Die Einheit ergibt sich, wenn man
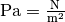 und
und
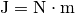 setzt. Die resultierende Dichte der Luft
im Laborvakuum ist also, verglichen mit der normalen Luftdichte von rund
setzt. Die resultierende Dichte der Luft
im Laborvakuum ist also, verglichen mit der normalen Luftdichte von rund
![\unit[1,29]{\frac{kg}{m^3}}](../_images/math/7722e4d529b6496f0bda64f7f2e3aadae9bf43c5.png) , äußerst gering.
, äußerst gering.In einem Kubikzentimeter dieses Restgases befindet sich bei gleicher Dichte nur ein Millionstel dieser Masse, also
![\unit[1,19 \cdot 10 ^{-18}]{g}](../_images/math/a19585353186bccc804815acdef9decd9927f1ec.png) .
Anhand der molaren Masse
.
Anhand der molaren Masse ![m_{\mathrm{M}} = \unit[29]{\frac{g}{mol}}](../_images/math/f7be9860f55837f4830aeff2486e98efea6a38df.png) von
Luft folgt damit für die enthaltene Stoffmenge:
von
Luft folgt damit für die enthaltene Stoffmenge:![n = \frac{m}{m_{\mathrm{M}}} = \frac{\unit[1,19 \cdot 10
^{-18}]{g}}{\unit[29]{\frac{g}{mol}}} \approx \unit[4,11 \cdot 10
^{-20}]{mol}](../_images/math/032bafbcc54b5cf2c0f567b74c7a28bb5c7f3582.png)
In einem Mol sind
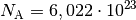 Teilchen
enthalten. Somit gilt für die Anzahl
Teilchen
enthalten. Somit gilt für die Anzahl 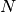 der je Kubikzentimeter im Gefäß
verbleibenden Teilchen:
der je Kubikzentimeter im Gefäß
verbleibenden Teilchen:![N = n \cdot N_{\mathrm{A}} = \unit[4,11 \cdot 10 ^{-20}]{mol} \cdot
\unit[6,022 \cdot 10 ^{23}]{\frac{1}{mol}} \approx 24,7 \cdot 10^3](../_images/math/21385d9ae1deca1ac3bd371f0fb5a5159f64bfd4.png)
In diesem „Laborvakuum“ sind also immer noch rund
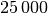 Luftteilchen
je Kubikzentimeter enthalten.
Luftteilchen
je Kubikzentimeter enthalten.
| [1] | Beim Aufpumpen eines Balles oder eines Fahrrad-Schlauches ist sich dieser Effekt gut spürbar, da in diesem Fall das Ventil erst öffnet, wenn der Luftdruck in der Pumpe höher ist als in der Umgebung (innerhalb des Balles bzw. des Schlauches). Eine ähnliche Wirkung lässt sich beobachten, wenn die Luftpumpe während des Pumpens mit einem Finger zugedrückt wird. |
| [2] | Beispielsweise zieht sich ein bei Zimmertemperatur aufgeblasener Luftballon zusammen, wenn man ihn in Eiswasser taucht. |
| [3] | Viele Gase – insbesondere Edelgase – lassen sich durch das Modell des
idealen Gases allerdings bis zu sehr tiefen Temperaturen sehr gut
beschreiben (unter Normaldruck siedet Sauerstoff beispielsweise bei
![\unit[-183]{\degree C}](../_images/math/bed9f06e7ec213661ca13aca38ba617398a769f7.png) , Helium erst bei , Helium erst bei ![\unit[-269]{\degree C
}](../_images/math/3605373b46cbe0e14ef732c522743757810890c7.png) ). ). |
