Dynamik¶
Mechanische Kräfte¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Mechanische Kräfte.
Bremst man beim Fahrradfahren abrupt mit der Vorderbremse, so ähnelt dies einer Fahrt gegen eine hohe Bordsteinkante: Der Fahrer, der Fahrrad-Rahmen sowie das ungebremste Hinterrad behalten aufgrund ihrer Massenträgtheit ihre ursprüngliche Bewegungsrichtung und (zunächst) auch ihre Geschwindigkeit bei.
Da der Weg nach vorne „blockiert“ ist, ähnelt die Situation eher einem (schwungvollen) Hebelarm, der sich um eine feste Drehachse bewegt: Durch die Trägheit seiner Masse wird der Fahrer im schlimmsten Fall über die Lenkstange katapultiert. Die Vorderbremse sollte daher stets mit Bedacht und möglichst nur als „Unterstützung“ der Hinterrad-Bremse eingesetzt werden..
Während des Bremsens spürt ein Fahrgast seine Trägheitskraft und drückt unbewusst nach hinten. Der plötzliche Wegfall der Trägheitskraft beim Anhalten wird jedoch nicht schnell genug bemerkt, und der Körper gibt rückwärts nach.
Da der Einkaufswagen starr ist, können Zug- und Druckkräfte an ihm keine Verformung, sondern lediglich eine Veränderung seiner Geschwindigkeit hervorrufen. Wird der Wagen exakt im rechten Winkel zu seiner Querachse geschoben oder gezogen, so liegen die Wirkungslinien der jeweiligen Kraft auf einer Linie. In diesem Fall wird der Wagen durch gleich große Zug- oder Druckkräfte in gleichem Maße beschleunigt.
Kraft und Gegenkraft haben immer die gleiche Wirkungslinie, aber unterschiedliche Richtungen. Sie treten an allen Stellen auf, an denen Kräfte übertragen werden.
In den drei abgebildeten Fällen wirken jeweils Gewichtskräfte, denen jweils eine Auflagekraft des Bodens oder eine Haltekraft (des Armes bzw. der Decke) entgegen wirken. Im mittleren Teil der Abbildung könnte für jedes im Regal stehende Buch ein eigener Kraftpfeil eingezeichnet werden. Die Wirkung der einzelnen Gewichtskräfte auf den Boden ist allerdings mit der im Schwerpunkt wirkenden Gesamtkraft identisch. Da sich die Gewichtskraft gleichmäßig auf zwei Punkte verteilt, sind dort die Längen (Beträge) der Kraft-Gegenkraft-Pfeile nur halb so groß.
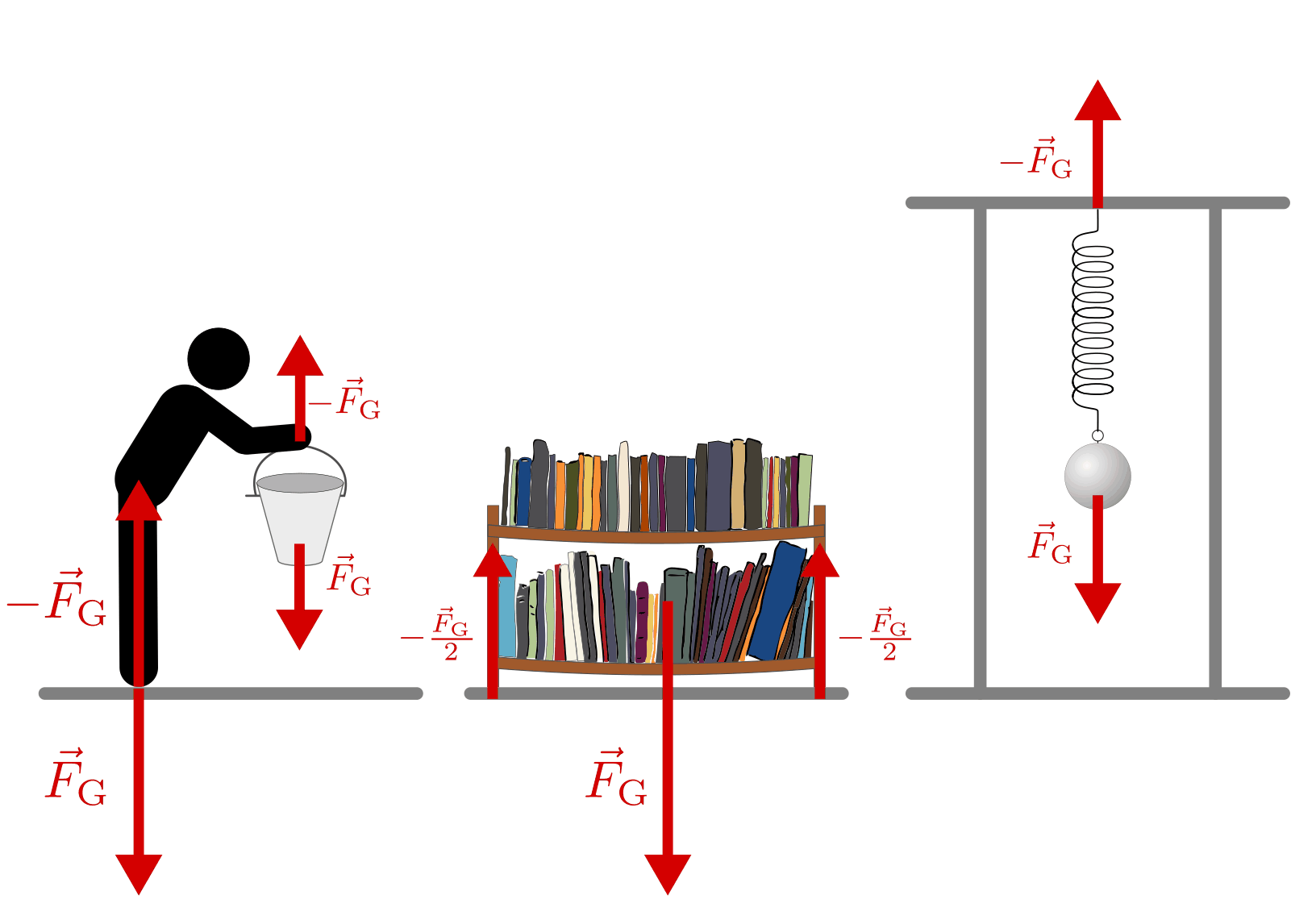
SVG: Kraft und Gegenkraft 1 (Lösung)Im rechten Teil der Abbildung müssten korrekterweise zwei Kraftpaare eingezeichnet werden: Einerseits zieht die Kugel mit ihrer Gewichtskraft an der Feder und dehnt diese dabei, gleichzeitig hält die Feder die Kugel und hindert sie am Herunterfallen. Andererseits ziehen Kugel und Feder gemeinsam an der Decke, die wiederum mit ihrer Haltekraft entgegenwirkt. Die obige Darstellung kann in der vereinfachten Form nur dann genutzt werden, wenn das Gewicht der Feder gegenüber dem Gewicht der Kugel vernachlässigt werden kann.
Zusammenwirken mehrerer Kräfte¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Zusammenwirken mehrerer Kräfte.
Die Gewichtskraft
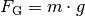 des Kindes
des Kindes ![(m =
\unit[30]{kg})](../../_images/math/7d705aae128fd7aa5df67f29822796c6c679139c.png) verteilt sich gleichmäßig auf beide Seilstücke. Somit gilt
für die Kraft
verteilt sich gleichmäßig auf beide Seilstücke. Somit gilt
für die Kraft 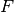 in jedem der beiden Seile:
in jedem der beiden Seile:![F = \frac{1}{2} \cdot F_{\mathrm{G}} = \frac{1}{2} \cdot \unit[30]{kg}
\cdot \unit[9,81]{\frac{N}{kg}} = \unit[147,15]{N}](../../_images/math/658c63fdcc53ec84581c2e2f63fd4f0dccbd98c4.png)
In beiden Seilen wirkt somit eine Zugkraft von rund
![\unit[147]{N}](../../_images/math/192b8e5b3cf744850eaeb8459bd03365fd04479d.png) .
.
Zeichnerisch findet man die Gesamtkraft
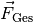 , indem
man ein Kräfteparallelogramm durch durch paralleles Verschiebung der beiden
Kraftpfeile konstruiert. Die gesuchte Gesamtkraft entspricht der Diagonalen
des Kräfteparallelogramms.
, indem
man ein Kräfteparallelogramm durch durch paralleles Verschiebung der beiden
Kraftpfeile konstruiert. Die gesuchte Gesamtkraft entspricht der Diagonalen
des Kräfteparallelogramms.(Es würde bereits genügen, nur einen Pfeil parallel an die Spitze des anderen zu verschieben. Durch Bildung eines Kräfteparallelogramms erhöht sich bei Zeichnungen von Hand allerdings die Genauigkeit.)
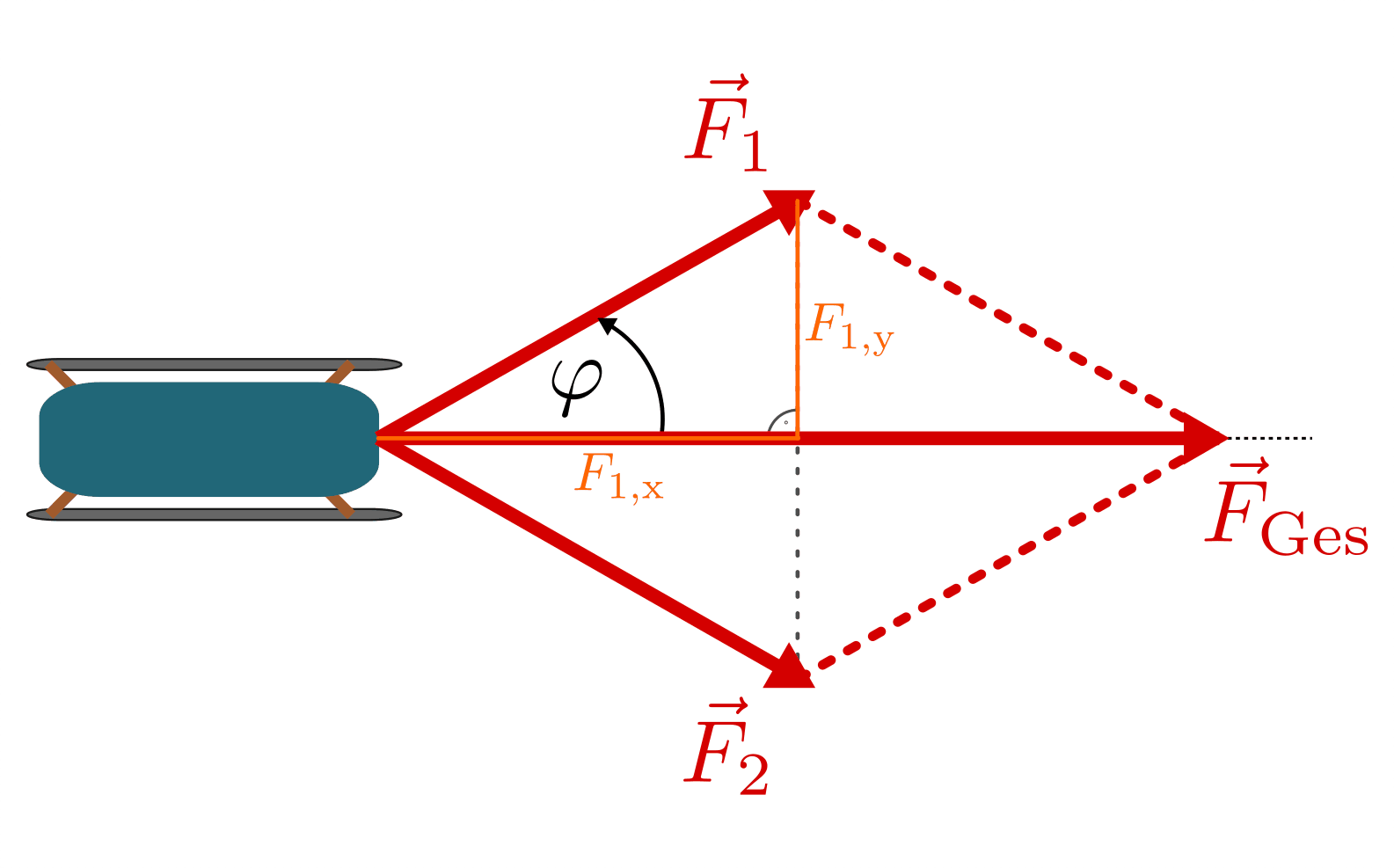
SVG: Kraftaddition Schlitten (Lösung)Rechnerisch lässt sich die Aufgabe lösen, indem man den Kräfte
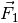 und
und 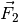 mit Hilfe der trigonometrischen
Funktionen
mit Hilfe der trigonometrischen
Funktionen 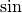 und
und  in jeweils eine
in jeweils eine 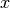 - und
eine
- und
eine 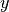 -Komponente aufteilt.
-Komponente aufteilt.Für die Kraft
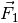 gilt:
gilt:![F_{\mathrm{1,x}} = \unit[40]{N} \cdot \cos{(30\degree)} \approx \unit[35]{N}\\
F_{\mathrm{1,y}} = \unit[40]{N} \cdot \sin{(30\degree)} \approx \unit[20]{N}\\](../../_images/math/666154d6e7e4786a17046ff5128f9e6561d61ebd.png)
Für die Kraft
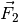 gilt:
gilt:![F_{\mathrm{2,x}} &= \unit[40]{N} \cdot \cos{(30\degree)} \approx \unit[35]{N}\\
_{\mathrm{2,y}} &= \unit[40]{N} \cdot \,\sin{(30\degree)} \approx \unit[-20]{N}\\](../../_images/math/0e3ec492d2493c0b53af2a4f7384e7512a554c88.png)
Das Minuszeichen der Kraftkomponente
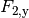 gibt an, dass die
Kraft entgegen der als positiv festgelegten
gibt an, dass die
Kraft entgegen der als positiv festgelegten 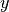 -Richtung verläuft. Um
beide Kräfte zu addieren, werden die
-Richtung verläuft. Um
beide Kräfte zu addieren, werden die 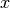 - und die
- und die
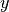 -Komponenten beider Kräfte addiert. Es ergibt sich:
-Komponenten beider Kräfte addiert. Es ergibt sich:![F_{\mathrm{1,x}} + F_{\mathrm{2,x}} = \unit[35]{N} &+ \unit[35]{N} =
\unit[70]{N} \\
F_{\mathrm{1,y}} + F_{\mathrm{2,y}} = \unit[20]{N} &- \unit[20]{N} =
\unit[0]{N} \\](../../_images/math/27e3ecb924262aa4084aea7c9015de3d54bdcdb5.png)
Die Gesamtkraft
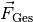 hat somit einen Betrag von
rund
hat somit einen Betrag von
rund ![\unit[70]{N}](../../_images/math/1913306ab3dcbfa6c033a08d4cd19235e0a0b3ca.png) und verläuft in die positive
und verläuft in die positive 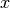 -Richtung.
-Richtung.
Bei einer Gleitreibungszahl von
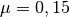 ergibt sich aus der
Gewichtskraft
ergibt sich aus der
Gewichtskraft ![F_{\mathrm{G}} = \unit[500]{N}](../../_images/math/359aca12771ea2968879f842eec7209311b5e5d4.png) folgende Reibungskraft
folgende Reibungskraft
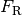 :
:![F_{\mathrm{R}} = \mu \cdot F_{\mathrm{G}} = 0,15 \cdot \unit[500]{N} = \unit[75]{N}](../../_images/math/7ceef18f2f901d37369840ecf069f448ec687b04.png)
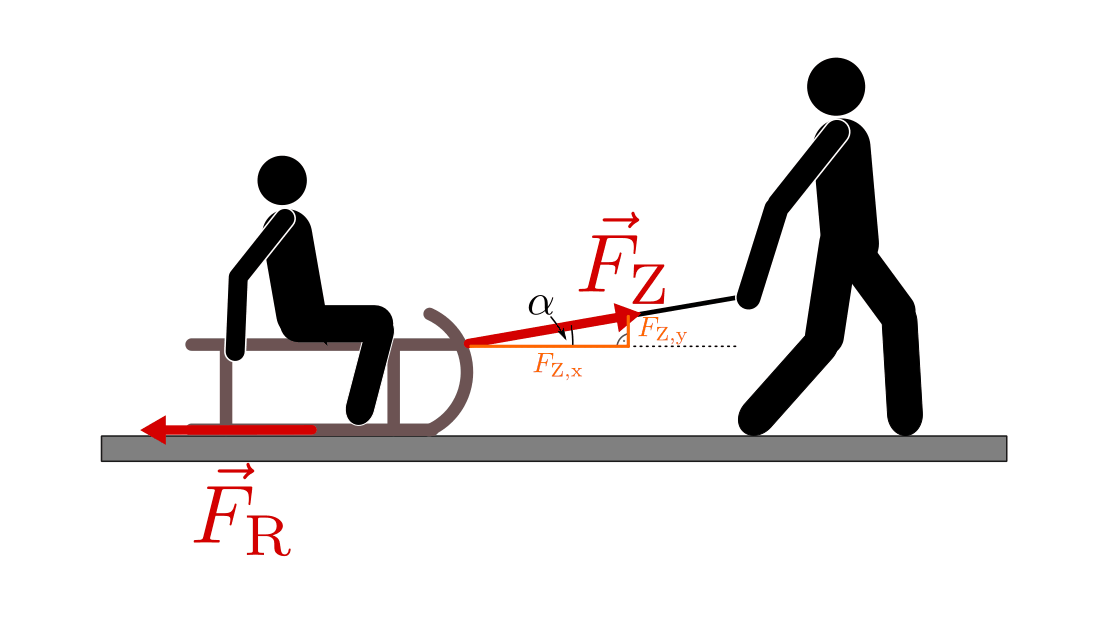
SVG: Kraftzerlegung beim Ziehen eines Schlittens (Lösung)Wird der Schlitten mit konstanter Geschwindigkeit gezogen, so muss diese Reibungskraft von der horizontalen Komponente der Zugkraft ausgeglichen werden. Für die horizontale bzw. vertikale Komponente der Zugkraft gilt:
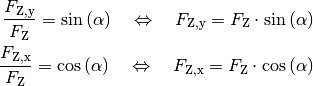
Für den Betrag der Zugkraft gilt somit
![F_{\mathrm{Z}} =
\frac{F_{\mathrm{Z,x}}}{\cos{(\alpha)}} = \frac{\unit[75]{N}}{\cos{(10
\degree)}} \approx \unit[76,2]{N}](../../_images/math/b69b810d547c35132b9af50b05dd1a08a59ec2a5.png) .
.
Wenn ein Kräfte-Gleichgewicht herrscht, so bilden die beteiligten Kräfte eine geschlossene Vektorkette; im Fall dreier Kräfte lassen sich die Vektoren zu einem Kräfte-Dreieck anordnen. Um die Winkel
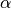 ,
, 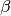 und
und 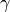 in diesem Dreieck zu bestimmen, kann der Cosinus-Satz genutzt werden. Hierbei gilt:
in diesem Dreieck zu bestimmen, kann der Cosinus-Satz genutzt werden. Hierbei gilt:![F_1^2 &= F_2^2 + F_3^2 - 2 \cdot F_2 \cdot F_3 \cdot \cos{(\alpha)} \quad
\Leftrightarrow \quad \alpha = \text{acos}\left( \frac{F_2^2 + F_3^2 -
F_1^2}{2 \cdot F_2 \cdot F_3}\right) \\[4pt]
F_2^2 &= F_3^2 + F_1^2 - 2 \cdot F_3 \cdot F_1 \cdot \cos{(\beta)} \quad
\Leftrightarrow \quad \beta = \text{acos}\left( \frac{F_3^2 + F_1^2 -
F_2^2}{2 \cdot F_3 \cdot F_1}\right) \\[4pt]
F_3^2 &= F_1^2 + F_2^2 - 2 \cdot F_1 \cdot F_2 \cdot \cos{(\gamma)} \quad
\Leftrightarrow \quad \gamma = \text{acos}\left( \frac{F_1^2 + F_2^2 -
F_3^2}{2 \cdot F_1 \cdot F_2}\right)](../../_images/math/1a66c60bc72d4d47391b1d26b8b6abbb6ebc7608.png)
Mit
![F_1 = \unit[50]{N}](../../_images/math/75ad86317c69d17efe00e86df6d643945dc9f54b.png) ,
, ![F_2 = \unit[70]{N}](../../_images/math/ebcf5e16a88de4414c5d857a741b84ee072765c0.png) und
und ![F_3 =
\unit[90]{N}](../../_images/math/dbc34878ad86068afe293d8e4112504ea61f7740.png) folgt:
folgt: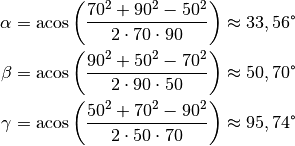
In Summe ergeben die obigen Winkel
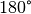 . Die Winkel zwischen
drei in einem Punkt wirkenden Kräften beträgt jedoch
. Die Winkel zwischen
drei in einem Punkt wirkenden Kräften beträgt jedoch 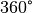 , die
„richtigen“ Winkel
, die
„richtigen“ Winkel 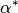 ,
, 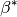 und
und 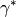 entsprechen also den zu den obigen Winkeln gehörenden Außenwinkeln. Sie
lassen sich berechnen, indem man für jeden Innenwinkel des Dreiecks die
Differenz zu
entsprechen also den zu den obigen Winkeln gehörenden Außenwinkeln. Sie
lassen sich berechnen, indem man für jeden Innenwinkel des Dreiecks die
Differenz zu 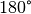 bildet:
bildet: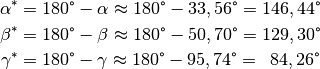
Für die Summe dieser Winkel gilt schließlich
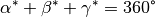 .
.
Da die Laterne symmetrisch aufgehängt ist, müssen die Kräfte
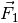 und
und 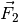 im linken und im rechten Seilstück
betragsmäßig gleich sein. Jedes der beiden Seilstücke muss somit in
vertikaler Richtung die Hälfte des Gewichtskraft
im linken und im rechten Seilstück
betragsmäßig gleich sein. Jedes der beiden Seilstücke muss somit in
vertikaler Richtung die Hälfte des Gewichtskraft ![F_{\mathrm{G}} =
\unit[50]{N}](../../_images/math/17933ad318141baa3e47e453d647a0761f8e4de9.png) der Lampe ausgleichen:
der Lampe ausgleichen:![F_{\mathrm{1,y}} &= F_{\mathrm{2,y}} \\
F_{\mathrm{1,y}} + F_{\mathrm{2,y}} &= \unit[50]{N}\\[8pt]
\Rightarrow F_{\mathrm{1,y}} = F_{\mathrm{2,y}} &= \unit[25]{N}](../../_images/math/1ff03d072878b874dde3e16cd223836119d86da6.png)
Die Größe der horizontalen Kraftkomponente kann graphisch mit Hilfe eines Kräfte-Parallelogramms oder rechnerisch mit Hilfe der trigonometrischen Funktionen anhand des Winkels
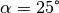 bestimmt werden.
bestimmt werden.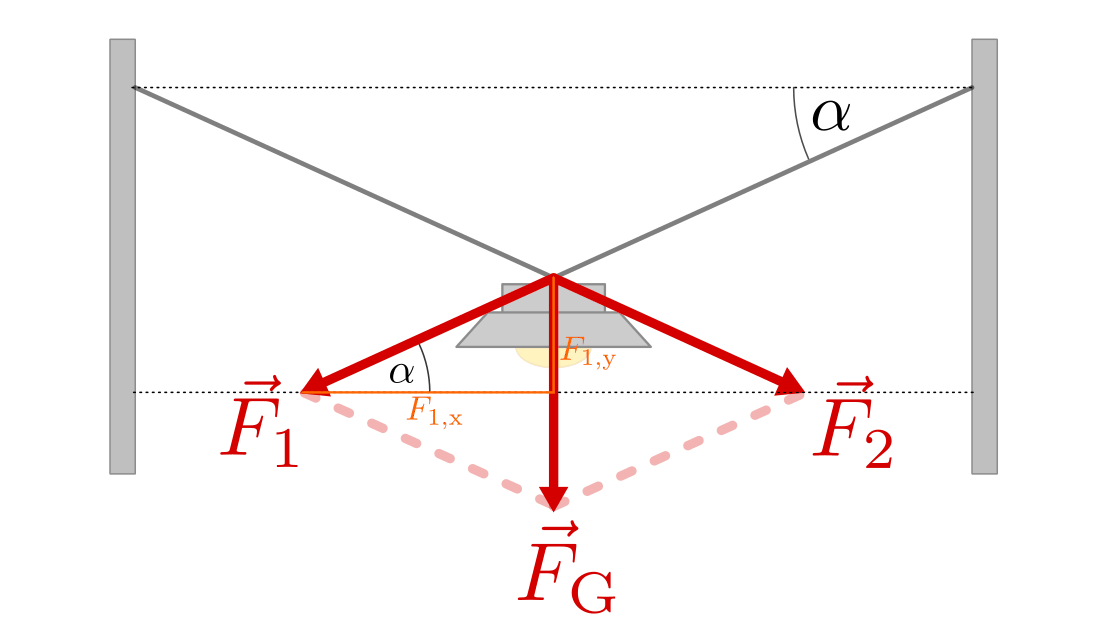
SVG: Kraftzerlegung am Beispiel einer Straßenlaterne (Lösung)Der Winkel zwischen
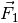 bzw.
bzw. 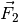 und der
Horizontalen ist ebenfalls gleich
und der
Horizontalen ist ebenfalls gleich 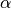 , da es sich um
Z-Winkel handelt.
Betrachtet man in der obigen Abbildung das orange hervorgehobene Dreieck, so
lässt sich die horizontale Komponente
, da es sich um
Z-Winkel handelt.
Betrachtet man in der obigen Abbildung das orange hervorgehobene Dreieck, so
lässt sich die horizontale Komponente 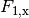 anhand der
folgenden Beziehung ausdrücken:
anhand der
folgenden Beziehung ausdrücken:![\frac{F_{\mathrm{1,y}}}{F_{\mathrm{1,x}}} = \tan{(\alpha)} \qquad
&\text{oder} \qquad \frac{F_{\mathrm{1,x}}}{F_{\mathrm{1,y}}} =
\cot{(\alpha)} \\[8pt]
\Rightarrow F_{\mathrm{1,x}} &= F_{\mathrm{1,y}} \cdot \text{cot}(\alpha)](../../_images/math/20c0787b9a79d5cc11aa10fc0688e95c26a20999.png)
Mit dem Cotangens-Wert
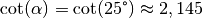 folgt somit
folgt somit ![F_{\mathrm{1,x}} \approx \unit[53,61]{N}](../../_images/math/90361fa2501b718fddd7fc555966b30677bd0a46.png) .
Der Kraftanteil
.
Der Kraftanteil 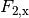 ist ebenso groß, zeigt aber in die
entgegengesetzte Richtung.
ist ebenso groß, zeigt aber in die
entgegengesetzte Richtung.
Mit
![h= \unit[1]{m}](../../_images/math/0a7f7d0ed857419165b27930ee761d872ea90152.png) ,
, ![l_1 = \unit[5]{m}](../../_images/math/ad4fcde2101dc4fba8958805ec1da03ff79005da.png) und
und ![l_2 =
\unit[10]{m}](../../_images/math/6193843f1db23946336be74da1071cf0ebeebb49.png) lassen sich die Größen der Winkel
lassen sich die Größen der Winkel 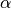 und
und
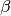 folgendermaßen berechnen:
folgendermaßen berechnen:![\tan{(\alpha)} = \frac{\unit[1]{m}}{\unit[10]{m}} \quad &\Leftrightarrow
\quad \alpha = \text{atan}\left(\frac{1}{10}\right) \approx \phantom{1}5,7
\degree \\[8pt]
\tan{(\beta)} = \frac{\unit[1]{m}}{\unit[5]{m}} \quad &\Leftrightarrow
\quad \beta = \text{atan}\left(\frac{1}{5}\right) \approx 11,3 \degree](../../_images/math/22f12a9f1a4ddbb4729b88fe6ec50cc5d53cfcb9.png)
Um die Beträge
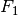 und
und 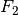 der zwei unbekannten Kräfte zu
berechnen, kann man ein Gleichungssystem der wirkenden Kräfte aufstellen.
Dabei lassen sich als Bedingungen nutzen, dass die vertikalen Anteile der
Kräfte in Summe die Gewichtskraft
der zwei unbekannten Kräfte zu
berechnen, kann man ein Gleichungssystem der wirkenden Kräfte aufstellen.
Dabei lassen sich als Bedingungen nutzen, dass die vertikalen Anteile der
Kräfte in Summe die Gewichtskraft ![F_{\mathrm{G}} = \unit[50]{N}](../../_images/math/83a4ffc3e9a705f7bd4d3c38811fcaee5cd15199.png) der Lampe
ausgleichen, und sich die horizontalen Anteile der Kräfte zu Null addieren. Es
muss also gelten:
der Lampe
ausgleichen, und sich die horizontalen Anteile der Kräfte zu Null addieren. Es
muss also gelten:![F_1 \cdot \sin{(\alpha)} + F_2 \cdot \sin{(\beta)} &= \unit[50]{N} \\
-F_1 \cdot \cos{(\alpha)} + F_2 \cdot \cos{(\beta)} &=
\unit[\phantom{5}0]{N} \\](../../_images/math/5b4e9d3ed92821f556b1394cd6b290342d52e8ce.png)
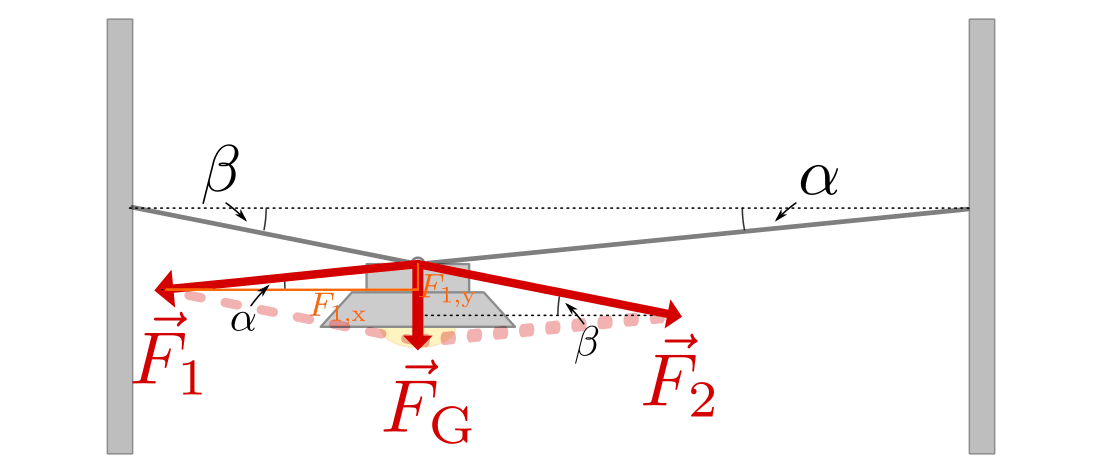
SVG: Asymmetrische Kraftzerlegung am Beispiel einer Straßenlaterne (Lösung)Um dieses Gleichungssystem zu lösen, kann beispielsweise die zweite Gleichung nach
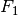 aufgelöst werden:
aufgelöst werden: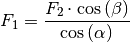
Dieser Ausdruck für
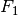 kann anschließend in die erste Gleichung
eingesetzt werden. Es folgt:
kann anschließend in die erste Gleichung
eingesetzt werden. Es folgt:![\frac{F_2 \cdot \cos{(\beta)}}{\cos{(\alpha)}} \cdot \sin{(\alpha)} + F_2
\cdot \sin{(\beta)} &= \unit[50]{N} \\[5pt]
F_2 \cdot \left( \frac{\cos{(\beta)}}{\cos{(\alpha)}} \cdot \sin{(\alpha)}
+ \sin{(\beta)}\right) &= \unit[50]{N} \\[10pt]](../../_images/math/55e485887bf06bf05126d8c89c778ebe937b48c0.png)
Man erhält damit als allgemeine Lösungsformeln:
![\Rightarrow F_2 &= \frac{\unit[50]{N}}{\left(
\frac{\cos{(\beta)}}{\cos{(\alpha)}} \cdot \sin{(\alpha)} +
\sin{(\beta)}\right)}\\[5pt]
\Rightarrow F_1 &= \frac{\unit[50]{N}}{\left(
\frac{\cos{(\beta)}}{\cos{(\alpha)}} \cdot \sin{(\alpha)} +
\sin{(\beta)}\right)} \cdot \frac{\cos{(\beta)}}{\cos{(\alpha)}}](../../_images/math/eb50f634a23ceb5b3887a5fd48c268826f8ba0a2.png)
Setzt man hier
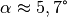 und
und 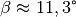 ein, so erhält man
ein, so erhält man ![F_2 \approx \unit[169,0]{N}](../../_images/math/4874edd6cb0b0d602102d449e8c885c818a2991d.png) und
und
![F_1 \approx \unit[167,5]{N}](../../_images/math/9415a0ae46bd88298e424b87476b45eda6f10dd3.png) .
.Diese Lösung kann ebenfalls (wesentlich schneller!) gefunden werden, wenn man feststellt, dass die in der folgenden Abbildung farblich hervorgehobenen Dreiecke kongruent sind. Damit folgt mit Hilfe des Sinus-Satzes unmittelbar:
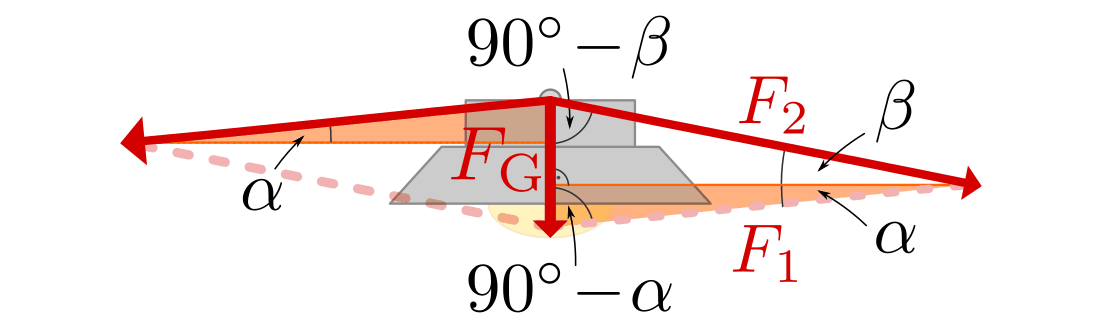
SVG: Asymmetrische Kraftzerlegung am Beispiel einer Straßenlaterne (Lösung)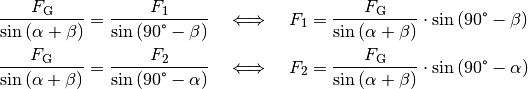
Auch hier liefert ein Einsetzen der Werte
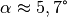 und
und 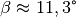 die Werte
die Werte ![F_1 \approx
\unit[167,5]{N}](../../_images/math/fc4eba16dea95f5b563c3f7b231051e7b5a05855.png) und
und ![F_2 \approx \unit[169,0]{N}](../../_images/math/4874edd6cb0b0d602102d449e8c885c818a2991d.png) .
.Die an den beiden Seilstücken ziehenden Kräfte sind also jeweils deutlich größer als die Gewichtskraft der Lampe. Da
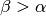 ist, hat die
Kraft
ist, hat die
Kraft 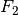 einen größeren Kraftteil in vertikaler Richtung als
einen größeren Kraftteil in vertikaler Richtung als
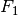 .
.
Arten mechanischer Kräfte¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Arten mechanischer Kräfte.
Um die Gewichtskraft
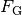 zu berechnen, die einer Masse
zu berechnen, die einer Masse
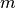 entspricht, muss diese mit dem jeweiligen Ortsfaktor
entspricht, muss diese mit dem jeweiligen Ortsfaktor 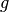 multipliziert werden. Für die Erde gilt mit
multipliziert werden. Für die Erde gilt mit ![m = \unit[1]{kg}](../../_images/math/a7f7cea70acf83856cbc0f17330ebc12d88f4937.png) und
und
![g_{\mathrm{Erde}} = \unit[9,81]{N/kg}](../../_images/math/d36df85432327788665ed05b2ee184b2650a2525.png) :
:![F_{\mathrm{G, Erde}} = \unit[1]{kg} \cdot \unit[9,81]{\frac{N}{kg} } =
\unit[9,81]{N}](../../_images/math/42749e29fe9e4f386df422e48e3c2ae56416970d.png)
Auf dem Mond gilt für den Ortsfaktor
![g_{\mathrm{Mond}} =
\unit[1,60]{\frac{N}{kg} }](../../_images/math/4823a799de155c15ff1c17daef976673ac91a4d7.png) und somit:
und somit:![F_{\mathrm{G, Mond}} = \unit[1]{kg} \cdot \unit[1,60]{\frac{N}{kg} } =
\unit[1,60]{N}](../../_images/math/b431b6fdda09300a1e22a5ab5e03eb03cd0eb080.png)
Die Gewichtskraft der
![\unit[1]{kg}](../../_images/math/09b7dde1c3df0c3397d37923b9d2712730211373.png) -Masse ist auf der Erde mit
-Masse ist auf der Erde mit
![F_{\mathrm{G, Erde}} = \unit[9,81]{N}](../../_images/math/766f867ceba7e956c39ac01a050f2b6742152afd.png) somit etwa
somit etwa 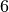 mal größer
als die Gewichtskraft
mal größer
als die Gewichtskraft ![F_{\mathrm{G, Mond}} = \unit[1,60]{N}](../../_images/math/c17c7a0cc00187f9fb48bdbf6e9db031a7ae9c47.png) der
gleichen Masse auf dem Mond.
der
gleichen Masse auf dem Mond.
Der Ortsfaktor auf dem Mond ist
![g_{\mathrm{Mond}} = \unit[1,60]{N/kg}](../../_images/math/fa59596c60949e91a1c19054ba0022a9b361512a.png) ,
der Ortsfaktor auf der Erde ist
,
der Ortsfaktor auf der Erde ist ![g_{\mathrm{Erde}} = \unit[9,81]{N/kg}](../../_images/math/d36df85432327788665ed05b2ee184b2650a2525.png) .
Der Astronaut spürt auf der Erde somit eine
.
Der Astronaut spürt auf der Erde somit eine 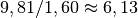 -fache Gewichtskraft:
-fache Gewichtskraft:![F_{\mathrm{G, Erde}} = \unit[130]{N} \cdot \frac{\unit[9,81]{\frac{N}{kg}
}}{\unit[1,60]{\frac{N}{kg} }} \approx \unit[130]{N} \cdot 6,13 \approx
\unit[797]{N}](../../_images/math/be5533fcf1e00f083b994e4cc80ae9b31c76cb6a.png)
Die Masse des Astronauten lässt sich berechnen, indem man seine Gewichtskraft durch den jeweiligen Ortsfaktor teilt:
![m = \frac{\unit[130]{N}}{\unit[1,60]{\frac{N}{kg} }} =
\frac{\unit[797]{N}}{\unit[9,81]{\frac{N}{kg} }} = \unit[81,25]{kg}](../../_images/math/270fe2a965d475b47aad479c6f711a24340d13ce.png)
Die Masse des Astronauten beträgt somit
![m = \unit[81,25]{kg}](../../_images/math/dc3c135dfd4826e48a45151e4375a6b44b29a709.png) .
.
Ohne Reibung würden die Füße – extremer als auf Eis – unkontrollierbar über den Boden gleiten.
Tatsächlich muss die Erde immer „dagegen halten“, wenn ein Körper (durch Muskelkraft oder einen Motor) in eine bestimmte Richtung beschleunigt werden soll. Ohne Reibung würde die Erde keine Kraft spüren, und damit wäre auch die Gegenkraft der Erde auf den Körper gleich Null. Der Körper erfährt somit keine Beschleunigung.
Um die Holzkiste in Bewegung zu versetzen, muss ihre Haftreibungskraft
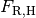 überwunden werden. Setzt man die Masse
überwunden werden. Setzt man die Masse ![m =
\unit[50]{kg}](../../_images/math/be32a7e351358d4b7bcaa58a64ed7a69d68e1c2f.png) und die Haftreibungszahl
und die Haftreibungszahl ![\mu_{\mathrm{H}} =
\unit[0,54]{}](../../_images/math/84eafaad8fdd197b12ee1a1d9af927fd34153761.png) in die Haftreibungs-Gleichung ein, so ergibt sich:
in die Haftreibungs-Gleichung ein, so ergibt sich:![F_{\mathrm{R,H}} = \mu_{\mathrm{H}} \cdot F_{\mathrm{G}} = 0,54 \cdot
\unit[50]{kg} \cdot \unit[9,81]{\frac{N}{kg}} \approx \unit[265]{N}](../../_images/math/fdd61a2f3e58d6d1f1e671567b9fcefbf220134a.png)
Es muss somit eine Kraft
![F \ge \unit[265]{N}](../../_images/math/0d72226cdc2156d83a35fa496cddcac33313c368.png) aufgebracht werden, um
die Kiste in Bewegung zu versetzen. Um das Gleiten aufrecht zu erhalten,
muss nur die Gleitreibungskraft
aufgebracht werden, um
die Kiste in Bewegung zu versetzen. Um das Gleiten aufrecht zu erhalten,
muss nur die Gleitreibungskraft 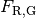 ausgeglichen werden:
ausgeglichen werden:![F_{\mathrm{R,G}} = \mu_{\mathrm{G}} \cdot F_{\mathrm{G}} = 0,34 \cdot
\unit[50]{kg} \cdot \unit[9,81]{\frac{N}{kg}} \approx \unit[167]{N}](../../_images/math/e667bba6f7eb2db3f9b50c8c33d581928b76a4d1.png)
Somit gilt für die zum (Weiter-)Gleiten der Kiste nötige Kraft
![F \ge
\unit[167]{N}](../../_images/math/c8096643da9a1746917d5cb71f229bcaddf1541d.png) .
.
Die Federkonstante
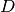 einer Schraubenfeder ist gleich dem Verhältnis
aus der auf sie wirkenden Kraft
einer Schraubenfeder ist gleich dem Verhältnis
aus der auf sie wirkenden Kraft 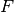 und der resultierenden
Längenänderung
und der resultierenden
Längenänderung 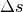 :
: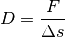
Setzt man die Werte
![F = \unit[1]{N}](../../_images/math/7e815340393dd687574138bb29a7c08b73951227.png) und
und ![\Delta s =
\unit[33]{cm} = \unit[0,33]{m}](../../_images/math/93f52c65f77e4fbb7438cbc6fa1fb25fe1d8116b.png) ein, erhält man:
ein, erhält man:![D = \frac{\unit[1]{N}}{\unit[0,33]{m}} = \unit[3,03]{\frac{N}{m} }](../../_images/math/9b1c6239d972edc1eb81c404ed588e0e8fab5697.png)
Die Federkonstante
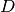 beträgt somit
beträgt somit ![\unitfrac[3,03]{N}{m}](../../_images/math/682b45dcc6e7d2cbfbd3c60c7dcd240de6d2f3b5.png) .
.
Für den Betrag der zum Dehnen einer Feder nötigen Spannkraft
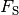 gilt mit
gilt mit ![D = \unitfrac[40]{N}{m}](../../_images/math/561b8f6a8469759ef9e4bb34d71554f38ba57cde.png) und
und ![s =
\unit[12]{cm} = \unit[0,12]{m}](../../_images/math/e3f7ba56ce915394a320d96d83be28990baae927.png) :
:![F_{\mathrm{S}} = D \cdot s = \unit[40]{\frac{N}{m} } \cdot \unit[0,12]{m}
= \unit[4,8]{N}](../../_images/math/925ef56e7619fee6551a738a3fd42ea1022ee5f9.png)
Es ist somit eine Kraft von
![\unit[4,8]{N}](../../_images/math/751633d72694979642e3c56b6cd8810f34af0639.png) nötig, um die
Schraubenfeder
nötig, um die
Schraubenfeder ![\unit[12]{cm}](../../_images/math/be40795c22bd6176c79d42fa974f8f2aafeb92c4.png) weit zu dehnen.
weit zu dehnen.
Die Dehnung
 einer Feder lässt sich anhand der bekannten
Federhärte
einer Feder lässt sich anhand der bekannten
Federhärte ![D = \unitfrac[650]{N}{m}](../../_images/math/299ada8b04e4c4bfe0e61b461e5ef4e770e78efa.png) und der wirkenden Kraft
und der wirkenden Kraft ![F =
\unit[20]{N}](../../_images/math/3b709e67eb07d6762c0b2f812d0be7a7e75691e2.png) wie folgt berechnen:
wie folgt berechnen: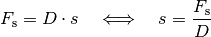
![s = \frac{F_{\mathrm{S}}}{D} = \frac{\unit[20]{N}}{\unit[650]{\frac{N}{m}
}} \approx \unit[0,031]{m}](../../_images/math/f41b6520bbd0aadaa5a32453c6bdc79a3e149523.png)
Die Schraubenfeder wird somit um
![\unit[0,031]{m} = \unit[3,1]{cm}](../../_images/math/97371c6ca61e2b50d53da129fd6f04c9fc13f4db.png) gedehnt.
gedehnt.
Damit das Fahrzeug nicht aus der Kurve gleitet, muss die Haftreibungskraft
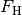 zwischen der Straße und den Reifen mindestens genauso
groß sein wie die zum Durchfahren der Kurve nötige Radialkraft
zwischen der Straße und den Reifen mindestens genauso
groß sein wie die zum Durchfahren der Kurve nötige Radialkraft
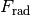 , es muss also gelten:
, es muss also gelten:![F_{\mathrm{H}} &= F_{\mathrm{rad}} \\[4pt]
\mu_{\mathrm{H}} \cdot m \cdot g &= m \cdot \frac{v^2}{r} \\
\Rightarrow r &= \frac{v^2}{\mu_{\mathrm{H}}\cdot g} \\](../../_images/math/f3e9028832e4ca2048b8d4b49380907917659d96.png)
Der Mindestradius
 der Kurvenbahn beim Durchfahren mit einer
bestimmten Geschwindigkeit
der Kurvenbahn beim Durchfahren mit einer
bestimmten Geschwindigkeit  ist also unabhängig von der
Fahrzeugmasse. Mit
ist also unabhängig von der
Fahrzeugmasse. Mit ![v = \unit[36]{km/h} = \unit[10]{m/s}](../../_images/math/869449de659cbb7d479720c63fffb05de3c508f0.png) ,
,
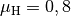 und
und ![g = \unit[9,81]{\frac{m}{s^2}}](../../_images/math/c64dddb2fc70d09e440b703a0826e8a4dc996987.png) folgt:
folgt:![r = \frac{v^2}{ \mu_{\mathrm{H}} \cdot g} =
\frac{\left(\unit[10]{\frac{m}{s}}\right)^2 }{0,8 \cdot
\unit[9,81]{\frac{m}{s^2}}} \approx \unit[12,75]{m}](../../_images/math/7a2a2335b88e695a64587f3519b77324d322e368.png)
Der Mindestradius beträgt somit knapp
![\unit[13]{m}](../../_images/math/213b32dad5025a07b1f7626e61ec1ab7094fc6c3.png) .
.
