Kinematik¶
Bewegungen mit konstanter Geschwindigkeit¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Bewegungen mit konstanter Geschwindigkeit.
Eindimensionale Bewegungen mit konstanter Geschwindigkeit
Alle Teil-Aufgaben können mittels der Formel
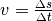 beziehungsweise
beziehungsweise 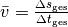 berechnet werden:
berechnet werden:Der Läufer legt eine Wegstrecke von
![\Delta s_{\mathrm{ges}} =
\unit[8,0]{km}](../../_images/math/45e429fcd31690a06c0a6d27312c74452f867e67.png) in einer Zeitspanne von
in einer Zeitspanne von ![\Delta t_{\mathrm{ges}} =
\unit[0,5]{h}](../../_images/math/b6562e4cb13bf461d6e535a0db2733b5a6045c9b.png) zurück. Somit beträgt seine Durchschnittsgeschwindigkeit:
zurück. Somit beträgt seine Durchschnittsgeschwindigkeit:![\bar{v} = \frac{\Delta s_{\mathrm{ges}}}{\Delta t_{\mathrm{ges}}} =
\frac{\unit[8,0]{km}}{\unit[0,5]{h}} = \unit[16]{\frac{km}{h}}](../../_images/math/08a4307a137c652d5fa078146ab57b43b9bb0500.png)
Der Radfahrer legt kontinuierlich
![\Delta s = \unit[36]{m}](../../_images/math/b6cf0c25e7b917c88447774cb0123bf19dafcfa6.png) in
in
![\Delta t = \unit[6]{s}](../../_images/math/159eed00c88a9acdd7cc951323b5ed73ddaf654d.png) zurück. Seine Geschwindigkeit beträgt damit:
zurück. Seine Geschwindigkeit beträgt damit:![v = \frac{\Delta s}{\Delta t} = \frac{\unit[36]{m}}{\unit[6]{s}} =
\unit[6]{\frac{m}{s}} = \unit[21,6]{\frac{km}{h}}](../../_images/math/f1bb76414dcde1b6cffb86962e2962941b9e4e51.png)
Bei der letzten Umrechnung wurde verwendet, dass
![\unit[1]{\frac{m}{s}} = \unit[3,6]{\frac{km}{h}}](../../_images/math/6c552a816f6e16c5dccb1dd20386c46d2455b846.png) ist.
ist.Der Weltrekord-Läufer legt
![\Delta s_{\mathrm{ges}}=\unit[100]{m}](../../_images/math/a77d131c0b640181794b2afd6b39efd0e9ad3653.png) in
in
![\Delta t_{\mathrm{ges}} = \unit[9,58]{s}](../../_images/math/85e3af0504cf47c1298b116b7bfd0f2ebe41dec5.png) zurück. Für seine
Durchschnittsgeschwindigkeit gilt damit:
zurück. Für seine
Durchschnittsgeschwindigkeit gilt damit:![\bar{v = \frac{\Delta s_{\mathrm{ges}}}{\Delta t_{\mathrm{ges}}}} =
\frac{\unit[100]{m}}{\unit[9,58]{s}} \approx \unit[10,44]{\frac{m}{s}}
\approx \unit[37,58]{\frac{km}{h}}](../../_images/math/db84cc812685445fa74d1ea91d9c8257a1cb5879.png)
Der Zug legt
![\Delta s_{\mathrm{ges}} = \unit[245]{km}](../../_images/math/1ab689a851f804abacf8a93c7d310fc72d2a3b07.png) in einer Zeit von
Zeit
in einer Zeit von
Zeit ![\Delta t_{\mathrm{ges}} = \unit[3,5]{h}](../../_images/math/bc1c3b0dbf18fcc5a4306e46b70a4c00a3ed6b48.png) zurück. Somit ergibt sich:
zurück. Somit ergibt sich:
![\bar{v} = \frac{\Delta s_{\mathrm{ges}}}{\Delta t_{\mathrm{ges}}} =
\frac{\unit[245]{km}}{\unit[3,5]{h}} = \unit[70]{\frac{km}{h}}](../../_images/math/846f0a28ddd5ba19a82385dde91cd1551a28c0d8.png)
Um die Wegstrecke zu berechnen, die das Auto in einer Sekunde zurücklegt, muss man die in
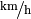 angegebene Geschwindigkeit in
angegebene Geschwindigkeit in
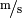 umrechnen:
umrechnen:![\unit[1]{\frac{km}{h} } = \unit[\frac{1}{3,6} ]{\frac{m}{s}} \quad
\Rightarrow \quad v = \unit[108]{\frac{km}{h}} =
\unit[\frac{108}{3,6}]{\frac{m}{s}} = \unit[30]{\frac{m}{s}}](../../_images/math/3cb8e27d1ac41f107fc347b364e349188ce4f662.png)
In einer Sekunde legt das Auto somit
![\unit[30]{m}](../../_images/math/ce1bdc6672ff6e003be09b314469fd92a6da2f94.png) zurück. Die Strecke,
die das Fahrzeugt in einer Minute
zurück. Die Strecke,
die das Fahrzeugt in einer Minute ![(\unit[60]{s})](../../_images/math/9e8ea6ffbf2b757a3852af98ce17b51c44b7995b.png) zurück legt, ist das
zurück legt, ist das
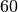 -fache dieser Strecke, also
-fache dieser Strecke, also ![\unit[1\,800]{m} =
\unit[1,80]{km}](../../_images/math/13916f92d431fce14c6dc1e129bb24f21c193046.png) .
.Um die Zeit zu berechnen, die man bei einer Geschwindigkeit von
![v=\unitfrac[5,0]{km}{h}](../../_images/math/5d94b85f8e642c724fa2bb388826662ecae3a1fb.png) für eine Strecke von
für eine Strecke von ![s=
\unit[800]{m}](../../_images/math/b1dce73933104dca3d81daa7c5e4055cc562b451.png) benötigt, muss die Geschwindigkeit wiederum in
benötigt, muss die Geschwindigkeit wiederum in
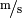 umgerechnet werden:
umgerechnet werden:![v = \unit[5,0]{\frac{km}{h}} = \unit[\frac{5,0}{3,6}]{\frac{m}{s}} =
\unit[1,39]{\frac{m}{s}}](../../_images/math/2258ff61231dc0130bf83c8408db3f1b127bb82d.png)
Löst man nun die Formel
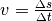 nach
nach
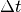 auf und setzt die obigen Werte ein, erhält man:
auf und setzt die obigen Werte ein, erhält man:![v &= \frac{\Delta s}{\Delta t} \quad \Leftrightarrow \quad \Delta t =
\frac{\Delta s}{v} \\[6pt]
\Delta t &= \frac{\unit[800]{m}}{\unit[1,39]{\frac{m}{s} }} \approx
\unit[576]{s}](../../_images/math/da783a151246af9c5e11fba4f424d3afc6ad6900.png)
Man benötigt somit etwa
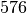 Sekunden (das entspricht rund
Sekunden (das entspricht rund
![\unit[9,6]{min}](../../_images/math/ede09bc5c7b395172d7b7a70dc385be4587d8731.png) ).
).Um die benötigte Zeit zu berechnen, die das Licht von der Sonne bis zur Erde benötigt, muss die Geschwindigkeitsformel
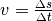 wieder nach der Zeitdauer
wieder nach der Zeitdauer 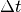 aufgelöst werden:
aufgelöst werden:
Die Strecke, die das Licht von der Sonne bis zur Erde zurücklegt, beträgt
![\Delta s = \unit[150\,000\,000]{km}](../../_images/math/300b07cd22bd3d79f9ff3c7ce2b884c449a32fe4.png) . Die Geschwindigkeit des Lichts
liegt bei
. Die Geschwindigkeit des Lichts
liegt bei ![\unitfrac[300 000]{km}{s}](../../_images/math/9c515385ae5a218947571a5c963da46909016d63.png) . Eingesetzt ergibt sich:
. Eingesetzt ergibt sich:![\Delta t = \frac{\Delta s}{v} =
\frac{\unit[150\,000\,000]{km}}{\unit[300\,000]{\frac{km}{s} }} =
\unit[500]{s}= \unit[8]{min} \, \unit[20]{s}](../../_images/math/8d54bced18fa447a4d70dd25100abbb8607fb6a5.png)
Das Licht benötigt für seinen Weg zur Erde somit etwas mehr als
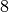 Minuten.
Minuten.
Um den vom Schall zurückgelegten Weg zu berechnen, muss die Geschwindigkeitsformel
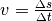 nach der
Wegstrecke
nach der
Wegstrecke 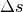 aufgelöst werden:
aufgelöst werden: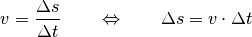
Die Zeit, welche der Schall auf seinem Weg zur Felswand und zurück benötigt, ist gleich
![\Delta t = \unit[5]{s}](../../_images/math/5c7e66fdeb3673ef124fcc7b71b961f4533cdf46.png) . Die Schallgeschwindigkeit in Luft
beträgt
. Die Schallgeschwindigkeit in Luft
beträgt ![v = \unitfrac[330]{m}{s}](../../_images/math/baf50a19de90679e6023f7473b48076bc719ab81.png) . Eingesetzt ergibt sich:
. Eingesetzt ergibt sich:![\Delta s = v \cdot \Delta t = \unit[330]{\frac{m}{s} } \cdot \unit[5]{s} =
\unit[1650]{m}](../../_images/math/b112c0fa31d8e572ad756d0ef4b7352ebb953471.png)
Die Gesamtstrecke, welche der Schall auf dem Hin- und Rückweg durchläuft, beträgt
![\unit[1650]{m}](../../_images/math/a4741935c1a4aea91b6fedd4f4edd89e2fc0455f.png) . Die Entfernung der Felswand vom Wanderer ist
gleich der Hälfte dieser Strecke, also rund
. Die Entfernung der Felswand vom Wanderer ist
gleich der Hälfte dieser Strecke, also rund ![\unit[0,8]{km}](../../_images/math/1a3ddd814176cdad6dad43fa538619c2983674d4.png) .
.
Je nach Betrachtungsweise sind zwei Aussagen möglich:
- Der Fahrgast ändert, genauso wie der Zug, seine Lage gegenüber dem Bahnhofsgebäude (als feststehend angenommen). Der Fahrgast ist in Bewegung.
- Der Fahrgast ändert nicht seine Lage gegenüber dem Abteil, in dem er sitzt. Der Fahrgast ist in Ruhe gegenüber dem Abteil.
Übrigens soll Albert Einstein einmal einen Schaffner gefragt haben: „Wann hält denn Ulm an diesem Zug?“
Die Wahl eines Bezugpunktes, gegenüber dem die weiteren Bewegungen beschrieben werden, ist frei und ändert nichts an den physikalischen Gesetzmäßigkeiten. Wir nehmen beispielsweise gerne auf der Erde ‚ruhende‘ Objekte als feste Bezugspunkte an, obwohl sich die Erde selbst mit ca.
![\unitfrac[30]{km}{s}](../../_images/math/6b0e6231a579857f0265705caf0ed050e8eadc0a.png) um die Sonne bewegt!
um die Sonne bewegt!
Wenn das Fahrzeug einen Läufer einholt, so ist die gleichbedeutend damit, dass zu diesem Zeitpunkt beide die gleiche Wegstrecken zurückgelegt haben, also
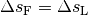 ist.
ist.Bis das Fahrzeug nach
![\Delta t = \unit[30]{min} = \unit[0,5]{h}](../../_images/math/6d6cc5db8c38d4642c3d9166cbe2f82349a5c755.png) startet, hat sich der Läufer mit
startet, hat sich der Läufer mit ![v_{\mathrm{L}} =
\unitfrac[15]{km}{h}](../../_images/math/897d2d7bf0627951a105c44643dcbe4bcfc5ae5f.png) einen „Vorsprung“ von
einen „Vorsprung“ von ![\unitfrac[15]{km}{h}
\cdot \unit[0,5]{h} = \unit[7,5]{km}](../../_images/math/a5d9661c0a1845135676f2f0745538972d3abbc0.png) erkämpft. Für den Treffpunkt muss damit
gelten:
erkämpft. Für den Treffpunkt muss damit
gelten:![\Delta s_{\mathrm{F}} &= \Delta s_{\mathrm{L}} \\
v_{\mathrm{F}} \cdot \Delta t &= v_{\mathrm{L}} \cdot \Delta t +
\unit[7,5]{km} \\](../../_images/math/361091cc3d23b235262aaadad7994f5447be183b.png)
Hierbei bezeichnet
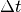 die Zeit, die ab dem Start des Fahrzeugs
vergeht. Die Gleichung enthält nur
die Zeit, die ab dem Start des Fahrzeugs
vergeht. Die Gleichung enthält nur 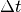 als unbekannte Größe und
kann somit unmittelbar aufgelöst werden:
als unbekannte Größe und
kann somit unmittelbar aufgelöst werden:![v_{\mathrm{F}} \cdot \Delta t - v_{\mathrm{L}} \cdot \Delta t &=
\unit[7,5]{km} \\ (v_{\mathrm{F}} - v_{\mathrm{L}}) \cdot \Delta t &=
\unit[7,5]{km} \\](../../_images/math/0d28302b3233000b9d390e8cb3bd8cf6f96d9f95.png)
![\Delta t &= \frac{\unit[7,5]{km}}{v_{\mathrm{F}} - v_{\mathrm{L}}} =
\frac{\unit[7,5]{km}}{\unit[(35-15)]{\frac{km}{h}}} = \unit[0,375]{h}\\](../../_images/math/01aaaaaa4fa1cd4d80c2df885ed1811b6e0f080a.png)
Das Fahrzeug ist bis zum Treffpunkt
![\Delta t = \unit[0,375]{h}](../../_images/math/5dadfa9096ae9ca42cc03c56ade27a72975e222f.png) unterwegs, bis es den Läufer einholt. In dieser Zeit legt es folgende Wegstrecke
zurück:
unterwegs, bis es den Läufer einholt. In dieser Zeit legt es folgende Wegstrecke
zurück:![\Delta s = v_{\mathrm{F}} \cdot \Delta t = \unit[35]{\frac{km}{h}} \cdot
\unit[0,375]{h} = \unit[13,125]{km}](../../_images/math/de8ed54d643f53c0ccee0a32284da3070b81d557.png)
In dieser Entfernung vom Startpunkt treffen sich der Läufer und das Fahrzeug also; der Läufer war insgesamt
![\unit[(0,5 + 0,375)]{h} =
\unit[0,875]{h}](../../_images/math/678dd4cec949ddc23d82b150a2ab88fd26ec4ec1.png) unterwegs.
unterwegs.Alternativ kann die Aufgabe auch mittels einer anders formulierten Bedingung für den Treffpunkt gelöst werden. Da das Fahrzeug immer eine konstante Geschwindigkeit hat und erst nach einer halben Stunde startet, könnte es ebenso zeitgleich starten, aber von einer Stelle aus, die sich
![\unitfrac[35]{km}{h} \cdot \unit[0,5]{h} = \unit[17,5]{km}](../../_images/math/f5b622852296f42867fd9bf78178361d2128568e.png) vor dem
Startpunkt befindet. Die Gleichung für den Treffpunkt kann also gleichwertig
folgendermaßen formuliert werden:
vor dem
Startpunkt befindet. Die Gleichung für den Treffpunkt kann also gleichwertig
folgendermaßen formuliert werden:![s_{\mathrm{F}} &= s_{\mathrm{L}} \\
v_{\mathrm{F}} \cdot t - \unit[17,5]{km} &= v_{\mathrm{L}} \cdot t \\](../../_images/math/b820f7c1f1adbe46c24c99c052f127b55f621aa5.png)
Hierbei bezeichnet
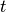 die insgesamt verstrichene Zeit, da beide
Fahrzeuge zum gleichen Zeitpunkt starten. Die Gleichung kann wiederum nach
die insgesamt verstrichene Zeit, da beide
Fahrzeuge zum gleichen Zeitpunkt starten. Die Gleichung kann wiederum nach
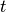 aufgelöst werden, man erhält dabei
aufgelöst werden, man erhält dabei ![t=\unit[0,875]{h}](../../_images/math/1a4e86599bd2a8102849da64ff29b0cedd82f737.png) .
.Eine dritte Lösungsmöglichkeit liegt darin, bei der Formulierung der Gleichung für den Treffpunkt die unterschiedlichen Startzeiten zu berücksichtigen. Eine so aufgestellte Gleichung lautet;
![v_{\mathrm{F}} \cdot (t - \unit[0,5]{h}) &= v_{\mathrm{L}} \cdot t](../../_images/math/fdb7d74ac7ffcacde6ccda3d19f5c417927b5817.png)
Bei dieser Formulierung wird berücksichtigt, dass das Fahrzeug insgesamt um
![\Delta t = \unit[30]{min} = \unit[0,5]{h}](../../_images/math/6d6cc5db8c38d4642c3d9166cbe2f82349a5c755.png) weniger lang unterwegs ist.
Löst man die Gleichung nach
weniger lang unterwegs ist.
Löst man die Gleichung nach 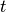 auf, erhält man wiederum
auf, erhält man wiederum ![t=
\unit[0,875]{h}](../../_images/math/5bd43bd3ba8e9924b36a3e29e8e1671e49ca7e28.png) als Ergebnis.
als Ergebnis.
Der Treffpunkt
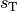 beider Fahrzeuge lässt sich bestimmen,
indem man die jeweiligen Ortsfunktionen aufstellt gleichsetzt. Wählt man ein
Koordinatensystem so, dass der Ort
beider Fahrzeuge lässt sich bestimmen,
indem man die jeweiligen Ortsfunktionen aufstellt gleichsetzt. Wählt man ein
Koordinatensystem so, dass der Ort 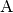 mit dem
Koordinatenursprung zusammenfällt und bezeichnet man die Richtung von
mit dem
Koordinatenursprung zusammenfällt und bezeichnet man die Richtung von
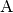 nach
nach 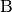 als „positiv“, so lauten die
Ortsfunktionen der beiden Fahrzeuge:
als „positiv“, so lauten die
Ortsfunktionen der beiden Fahrzeuge: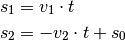
Die Geschwindigkeit des zweiten Fahrzeugs wird dabei negativ gewertet, da sie in die entgegengesetzte Richtung verläuft. Treffen sich beide Fahrzeuge, so ist
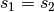 , und damit:
, und damit: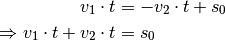
In dieser Gleichung kann auf der linken Seite
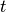 ausgeklammert werden.
Man erhält damit für die Zeit des Treffpunkts:
ausgeklammert werden.
Man erhält damit für die Zeit des Treffpunkts: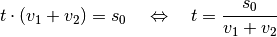
Setzt man die gegebenen Werte
![v_1 = \unitfrac[30,0]{km}{h}](../../_images/math/7e7f8f66c9bd056bcd6b93e3bb1b54d28c3adbad.png) ,
, ![v_2 =
\unitfrac[50,0]{km}{h}](../../_images/math/24365b3d84ea461c7b3ea4427926e52aee3be80e.png) und
und ![s_0 = \unit[100]{km}](../../_images/math/214ae17df9067ef011d273dd5460810380363462.png) in die obige Gleichung ein,
so erhält man:
in die obige Gleichung ein,
so erhält man:![t = \frac{s_0}{v_1 + v_2} = \frac{\unit[100]{km}}{\unit[30,0]{\frac{km}{h}}
+ \unit[50,0]{\frac{km}{h}}} = \unit[1,25]{h}](../../_images/math/8addfd043dc415ba43a611183ee7fc2d8981137c.png)
Beide Fahrzeuge treffen sich also nach
![t=\unit[1,25]{Stunden}](../../_images/math/b893c5028f7269826fd8e590904b85b37b8ece50.png) . Um die
Entfernung
. Um die
Entfernung  zu bestimmen, die beide Fahrzeuge zu diesem
Zeitpunkt vom Korrdinatenursprung (dem Ort
zu bestimmen, die beide Fahrzeuge zu diesem
Zeitpunkt vom Korrdinatenursprung (dem Ort 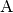 ) haben, kann man
diese Zeit in die Gleichung
) haben, kann man
diese Zeit in die Gleichung 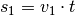 einsetzen und erhält:
einsetzen und erhält:![s = v_1 \cdot \unit[1,25]{h} = \unit[30,0]{\frac{km}{h}} \cdot
\unit[1,25]{h} = \unit[37,5]{km}](../../_images/math/227ec95775032f073a1e1c4be7a6e3bdef8cb3b6.png)
Beide Fahrzeuge treffen sich somit
![s=\unit[37,5]{km}](../../_images/math/ee38c060b459f7a172a43628c99045164078d2b9.png) vom Ort
vom Ort
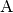 entfernt.
entfernt.
Mehrdimensionale Bewegungen mit konstanter Geschwindigkeit¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Mehrdimensionale Bewegungen mit konstanter Geschwindigkeit.
Um den
![s_y = \unit[100]{m}](../../_images/math/e3a64dbc9f8dc193f29859397d8cbb2e5ba097b8.png) breiten Fluss mit einer Geschwindigkeit von
breiten Fluss mit einer Geschwindigkeit von
![v_y = \unitfrac[0,5]{m}{s}](../../_images/math/096bd0c7760afc98e816e8418cebcdff8407e2be.png) zu überqueren, ist folgende Zeit nötig:
zu überqueren, ist folgende Zeit nötig:![v_y = \frac{s_y}{t} \quad \Longleftrightarrow \quad t = \frac{s_y}{v_y} =
\frac{\unit[100]{m}}{\unit[0,5]{\frac{m}{s}}} = \unit[200]{s}](../../_images/math/de949076a301b38e2d44ddbb2515dab4ccb49501.png)
In dieser Zeit wird der Schwimmer durch die Strömung um
![s_x=\unit[35]{m}](../../_images/math/ff5c2f7cff433c40528feb130e6c4e45ceb1bd17.png) abgetrieben. Die Strömungsgeschwindigkeit des
Flusses beträgt somit:
abgetrieben. Die Strömungsgeschwindigkeit des
Flusses beträgt somit:![v_x = \frac{s_x}{t} = \frac{\unit[35]{m}}{\unit[200]{s}} =
\unit[0,175]{\frac{m}{s}}](../../_images/math/7dd8a91796c0225b9cf71b6c1e713230a8a74769.png)
Dies entspricht einer (mittleren) Strömungsgeschwindigkeit von etwa
![\unitfrac[0,63]{km}{h}](../../_images/math/f99fc1faef1730ac427827e8dca1a884f595ec81.png) .
.
Im folgenden wird angenommen, dass sich das erste Objekt entlang der
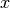 -Achse bewegt. Dann gilt für
-Achse bewegt. Dann gilt für 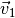 und
und 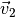 :
: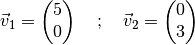
Der Betrag dieses Vektors ist
![|\vec{v}| = \sqrt{5^2 + 3^2} \approx
\unit[5,83]{\frac{m}{s}}](../../_images/math/5533fed3b5a2772cac46cff89f65a71334d0874f.png) . Nach
. Nach ![\Delta t = \unit[15]{s}](../../_images/math/2c74fe87e24b8ddedc88e902ec0e30edbd0a14e2.png) gilt für die
Ortskoordinaten
gilt für die
Ortskoordinaten 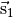 und
und 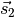 :
: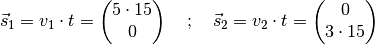
Die Entfernung beider Objekte voneinander ergibt sich aus der Differenz der beiden Ortsvektoren. Aus Sicht des ersten Gegenstands gilt:
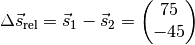
Der Betrag dieses Vektors ist:
![|\Delta \vec{s}_{\mathrm{rel}} | = \sqrt{75^2 + (-45)^2} \approx
\unit[87,5]{m}](../../_images/math/d5bddaca4aba1359978b10c756f2a09b0acca491.png)
Die Objekte sind nach
![\unit[15]{s}](../../_images/math/3996067f8456339ebc9823747c5875ada6844f79.png) somit rund
somit rund ![\unit[87,5]{m}](../../_images/math/8f18473c466f9e9bf6c0559ef0f85a8b96f00737.png) voneinander entfernt.
voneinander entfernt.
Bewegungen mit konstanter Beschleunigung¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Bewegungen mit konstanter Beschleunigung.
Eindimensionale Bewegungen mit konstanter Beschleunigung
Die Beschleunigung des Radfahrers ist gleich dem Verhältnis aus der Veränderung seiner Geschwindigkeit
![\Delta v = \unitfrac[30]{km}{h}
\approx \unitfrac[8,33]{m}{s}](../../_images/math/bae9c2b80cee51261963fd6b82189327395ec9ee.png) und der dafür benötigten Zeit
und der dafür benötigten Zeit ![\Delta t =
\unit[8,0]{s}](../../_images/math/25558464cc6da0934b241a3fb6bd799b795e14a9.png)
![a = \frac{\Delta v}{\Delta t} = \frac{\unit[8,33]{\frac{m}{s}}
}{\unit[8,0]{s}} \approx \unit[1,04]{\frac{m}{s^2} }](../../_images/math/def0708acdb4d52aaae8632e9688f65654da2047.png)
Die Beschleunigung des Radfahrers entspricht somit rund
![\unitfrac[1,0]{m}{s^2}](../../_images/math/c042376c31a2b0db4af2c75a62c82cd7731595aa.png) .
.
Die Geschwindigkeitsänderung
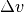 Fahrzeugs beträgt
Fahrzeugs beträgt
![\unitfrac[100]{km}{h} \approx \unitfrac[27,28]{m}{s}](../../_images/math/38dc7a05d826b64acee0d11cdceeb5668f4bd5b8.png) , die dafür
benötigte Zeit
, die dafür
benötigte Zeit ![\Delta t=\unit[10]{s}](../../_images/math/3bf5a117bdc086cc7abbdad86b7f71b673a0f959.png) . Für die Beschleunigung des
Fahrzeugs folgt somit:
. Für die Beschleunigung des
Fahrzeugs folgt somit:![a = \frac{\Delta v}{\Delta t} = \frac{\unit[27,78]{\frac{m}{s}}
}{\unit[10]{s}} \approx \unit[2,78]{\frac{m}{s^2} }](../../_images/math/1334459b09274b12d714fd3a9bbdbd2a2bfa6385.png)
Die Beschleunigung des Fahrzeugs beträgt also rund
![\unit[2,8]{m/s^2}](../../_images/math/a185d8c37f4274c8a5185e0faeee20cd8397d5d5.png) .
Die Beschleunigung beim Abbrems-Vorgang hat den gleichen Betrag, denn sowohl
die Geschwindigkeitsänderung
.
Die Beschleunigung beim Abbrems-Vorgang hat den gleichen Betrag, denn sowohl
die Geschwindigkeitsänderung 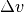 als auch die dafür benötigt Zeit
als auch die dafür benötigt Zeit
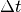 sind identisch. Der Beschleunigungswert trägt allerdings beim
Bremsvorgang ein negatives Vorzeichen, denn ein Abbremsen entspricht einer
Beschleunigung in die entgegengesetzte Richtung.
sind identisch. Der Beschleunigungswert trägt allerdings beim
Bremsvorgang ein negatives Vorzeichen, denn ein Abbremsen entspricht einer
Beschleunigung in die entgegengesetzte Richtung.
Die Geschwindigkeitsänderung des Fahrzeugs ergibt sich aus der Differenz zwischen der Endgeschwindigkeit
![v_2 = \unitfrac[36,5]{m}{s}](../../_images/math/694080501cd1f0e080a8d7938e2efa446ecd6290.png) (entspricht
(entspricht ![\unitfrac[131,4]{km}{h}](../../_images/math/ebafcb397431e6f885cbeea7846d0f65211c5d8a.png) ) und der Anfangsgeschwindigkeit
) und der Anfangsgeschwindigkeit
![v_1 = \unit[20,0]{m/s}](../../_images/math/86271e4995bd9d82846c7a866607e4204c8a4f13.png) (entspricht
(entspricht ![\unitfrac[72,0]{km}{h}](../../_images/math/9d276cd038261dcf63c59c376b35411874e963f3.png) ):
):![\Delta v = v_2 - v_1 = \unit[36,5]{\frac{m}{s} } -
\unit[20,0]{\frac{m}{s} } = \unit[16,5]{\frac{m}{s} }](../../_images/math/2193695cdd2f6f41e1e78c6a5ba17a166eef0b4c.png)
Teilt man diesen Wert durch die für die Geschwindigkeitsänderung benötigte Zeit
![t = \unit[5,0]{s}](../../_images/math/e85d955cfce9138668cd9f3dec384c3f16fe9df5.png) , so ergibt sich für die
Beschleunigung:
, so ergibt sich für die
Beschleunigung:![a = \frac{\Delta v}{\Delta t} = \frac{\unit[16,5]{\frac{m}{s}
}}{\unit[5,0]{s}} = \unit[3,3]{\frac{m}{s^2} }](../../_images/math/bf64fe6e5b1350b2d31557bbf9e58e4d60054cf8.png)
Die Beschleunigung des Fahrzeugs beträgt somit
![a =
\unitfrac[3,3]{m}{s^2}](../../_images/math/39019005a472a77671157b4554807b94983ab56e.png) . Vergleicht man diesen Wert mit dem Wert der
Erdbeschleunigung
. Vergleicht man diesen Wert mit dem Wert der
Erdbeschleunigung ![g = \unitfrac[9,81]{m}{s^2}](../../_images/math/365ec91ba3db2627d3ef86cb9edd14cf68aa7fcc.png) , so erkennt man, dass
ein Körper im freien Fall – sofern die Reibung vernachlässigbar ist – eine
rund dreifach höhere Beschleunigung erfährt als im beschleunigenden Fahrzeug.
, so erkennt man, dass
ein Körper im freien Fall – sofern die Reibung vernachlässigbar ist – eine
rund dreifach höhere Beschleunigung erfährt als im beschleunigenden Fahrzeug.Die Wegstrecke
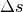 , die das Fahrzeug für den Beschleunigungsvorgang
benötigt, beträgt:
, die das Fahrzeug für den Beschleunigungsvorgang
benötigt, beträgt:![\Delta s = \frac{1}{2} \cdot a \cdot \Delta t^2 + v_1 \cdot \Delta t &=
\frac{1}{2} \cdot \unit[3,3]{\frac{m}{s^2} } \cdot (\unit[5,0]{s})^2 +
\unit[20]{\frac{m}{s}} \cdot \unit[5,0]{s} \\[4pt] &= \frac{1}{2} \cdot
\unit[3,3]{\frac{m}{s^2} } \cdot \;\; \unit[25]{s^2} \;\; + \unit[100]{m} \approx
\unit[141,25]{m}](../../_images/math/c844c589198af1340650b1afcfd34d742cf2afbe.png)
(Alternativ kann die für den Beschleunigungsvorgang benötigte Strecke auch mittels der „Bremsformel“
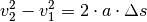 berechnet werden.)
berechnet werden.)Das Fahrzeug benötigt somit für den Beschleunigungsvorgang rund
![\unit[141]{m}](../../_images/math/9d85a919644f5b9b1d06cd4a1f535845abcd214f.png) .
.
Während der Reaktionszeit von
![\Delta t = \unit[1,0]{s}](../../_images/math/ae650455879aa09051dff820946763ffd1d0ac22.png) bewegt sich der
PKW mit seiner Anfangsgeschwindigkeit
bewegt sich der
PKW mit seiner Anfangsgeschwindigkeit ![v_0=\unitfrac[40]{km}{h} \approx
\unitfrac[11,1]{m}{s}](../../_images/math/87999c55f7f7ff39d299d744b1e95b378cc56c21.png) weiter; für den Reaktionsweg gilt also:
weiter; für den Reaktionsweg gilt also:![s_{\mathrm{Reaktion}} = v_0 \cdot \Delta t = \unit[11,1]{\frac{m}{s}}
\cdot \unit[1,0]{s} = \unit[11,1]{m}](../../_images/math/66dce6ca0a226b061f50724e3c008897092c27d2.png)
Der anschließende Bremsweg kann mittels der Bremsformel
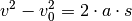 berechnet werden; da die
Endgeschwindigkeit
berechnet werden; da die
Endgeschwindigkeit  gleich Null ist, folgt:
gleich Null ist, folgt:![- v_0^2 = 2 \cdot a \cdot s_{\mathrm{Brems}} \quad \Longleftrightarrow
\quad s_{\mathrm{Brems}} = \frac{-v_0^2}{2 \cdot a} \\[5pt]
s_{\mathrm{Brems}} = \frac{-(\unit[11,1]{\frac{m}{s}})^2}{2 \cdot
(\unit[-4,5]{\frac{m}{s^2}})} \approx \unit[13,69]{m}](../../_images/math/5ece2851d3b47aa8aa2495861f5905e894df903c.png)
Der PKW kommt somit nach einem Anhalteweg von rund
![s_{\mathrm{Reaktion}} + s_{\mathrm{Brems}} = \unit[(11,1 + 13,69)]{m}
= \unit[24,8]{m}](../../_images/math/eb5f425a123bfd2413ccf3f85162f38d16a7f25d.png) gerade noch rechtzeitig vor dem Hindernis zum Stehen.
gerade noch rechtzeitig vor dem Hindernis zum Stehen.
Während des Sprungs wird der Badegast durch die Erdanziehung
![a = g =
\unitfrac[9,81]{m}{s^2}](../../_images/math/39c3ac4e6294b7b31dcb7d7d7acebadcd0f80f45.png) konstant beschleunigt. Um die Flugzeit zu bestimmen,
kann die Formel für die zurückgelegte Wegstrecke
konstant beschleunigt. Um die Flugzeit zu bestimmen,
kann die Formel für die zurückgelegte Wegstrecke ![s = \unit[5,0]{m}](../../_images/math/92b7525ae9deb6bc460a62780f6e887fd499ebe1.png) nach der Zeit
nach der Zeit 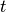 aufgelöst werden:
aufgelöst werden:
![t = \sqrt{\frac{2 \cdot s}{a} } = \sqrt{\frac{2 \cdot \unit[5,0]{m}
}{\unit[9,81]{\frac{m}{s^2}} } } \approx \unit[1,01]{s}](../../_images/math/0999af51adab4927c0380ef0f1458c425609849f.png)
Die Flugzeit beträgt somit rund
![\unit[1,0]{s}](../../_images/math/6388edef0d749bfe53a4f035d21fece8981d7e2b.png) . Die Geschwindigkeit
beim Eintauchen kann durch Einsetzen der (Erd-)Beschleunigung
. Die Geschwindigkeit
beim Eintauchen kann durch Einsetzen der (Erd-)Beschleunigung 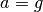 und der Flugzeit
und der Flugzeit 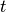 in die Gleichung
in die Gleichung 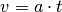 berechnet
werden:
berechnet
werden:![v = a \cdot t = \unit[9,81]{\frac{m}{s^2}} \cdot \unit[1,01]{s} \approx
\unit[9,9]{\frac{m}{s} }](../../_images/math/352509e185afe2214b7f0a8c708982c43bbe2b15.png)
Die Geschwindigkeit des Badegastes beim Eintauchen beträgt somit rund
![\unitfrac[9,9]{m}{s}](../../_images/math/9f9ce7da4da57917d47c93b0d6958e2ba77fbd4a.png) (entspricht
(entspricht ![\unitfrac[35,7]{km}{h}](../../_images/math/f607ad7662dbfc1b04941a883475e7a16342202a.png) ).
).
Der Stein wird, wenn der Luftwiderstand vernachlässigt werden kann, mit der konstanten Beschleunigung
![a = g = \unitfrac[9,81]{m}{s^2}](../../_images/math/36c86f50b8c1fc15b662105813a4b4ece1d7a316.png) beschleunigt. Die Endgeschwindigkeit
beschleunigt. Die Endgeschwindigkeit  ist gleich dem Produkt aus
der Beschleunigung und der Zeit
ist gleich dem Produkt aus
der Beschleunigung und der Zeit ![t = \unit[1,7]{s}](../../_images/math/de5bc293a00736c020ed3d483d481d76f20ebb5a.png) , während der die
Beschleunigung wirkt:
, während der die
Beschleunigung wirkt:![v = a \cdot t = \unit[9,81]{\frac{m}{s^2} } \cdot \unit[1,7]{s} \approx
\unit[16,67]{\frac{m}{s} }](../../_images/math/40c752aeca08a518b2122b410afc61cc15686e36.png)
Die Geschwindigkeit des Steins beträgt beim Aufprall somit rund
![\unitfrac[17]{m}{s} \approx~\unitfrac[60]{km}{h}](../../_images/math/1862de47cb76b1c588d72fd756ac3c8a203adb6d.png) . Bis zu diesem
Zeitpunkt legt der Stein folgende Wegstrecke
. Bis zu diesem
Zeitpunkt legt der Stein folgende Wegstrecke  zurück:
zurück:![s = \frac{1}{2} \cdot a \cdot t^2 = \frac{1}{2} \cdot
\unit[9,81]{\frac{m}{s^2} } \cdot (\unit[1,7]{s})^2 = \frac{1}{2} \cdot
\unit[9,81]{\frac{m}{s^2} } \cdot \unit[2,89]{s^2} \approx \unit[14,2]{m}](../../_images/math/c2ebc3bf66cda93ace4fd63f1db4caa31936838e.png)
Der Brunnen ist somit (mindestens)
![\unit[14]{m}](../../_images/math/f9bb79bbb2ea9f0fdcdce9d7b004e71fe37f2b02.png) tief.
tief.
Um die beim Aufprall wirkende Beschleunigung
 anhand des Bremsweges
(der „Knautschzone“)
anhand des Bremsweges
(der „Knautschzone“) ![\Delta s = \unit[0,5]{m}](../../_images/math/6d389f5edb382b4000481edaa47adb9e5080d830.png) zu ermitteln, kann die
Bremsformel
zu ermitteln, kann die
Bremsformel 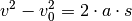 genutzt werden; die
Endgeschwindigkeit
genutzt werden; die
Endgeschwindigkeit  des Fahrzeugs ist dabei gleich Null, die
Beschleunigung erfolgt entgegen der Bewegungsrichtung und hat damit ein
negatives Vorzeichen.
des Fahrzeugs ist dabei gleich Null, die
Beschleunigung erfolgt entgegen der Bewegungsrichtung und hat damit ein
negatives Vorzeichen.Eine Geschwindigkeit von
![\unitfrac[30]{km}{h}](../../_images/math/8613f1b08e92d08475728ac9056c875f7162dcae.png) entspricht rund
entspricht rund
![\unitfrac[8,3]{m}{s}](../../_images/math/4f0962237bacbab2913995cc36b2a12c3b5d2dc6.png) . Eingesetzt in die Bremsformel ergibt sich
folgende Beschleunigung:
. Eingesetzt in die Bremsformel ergibt sich
folgende Beschleunigung:![| a | = \frac{v_0^2}{2 \cdot s} =
\frac{\left(\unit[8,3]{\frac{m}{s}}\right)^2}{2 \cdot \unit[0,5]{m}}
\approx \unit[69,4]{\frac{m}{s^2}}](../../_images/math/3287f1491350d8a3def7c154f843f2d39e39fc9e.png)
Eine Beschleunigung von
![\unitfrac[69,4]{m}{s^2}](../../_images/math/e62c917982988f2d900351d9fadf4fcd8e7ca8b5.png) entspricht etwa
entspricht etwa
![\unit[7,1]{g}](../../_images/math/0e5166af2eeb25c3ef93f9c301aa56de096d9c4b.png) , also einer gut siebenfachen Erdbeschleunigung. Dies
kann ein Mensch noch überleben, wenn auch mit erheblichen Verletzungen und
sogar Bewusstlosigkeit gerechnet werden muss.
, also einer gut siebenfachen Erdbeschleunigung. Dies
kann ein Mensch noch überleben, wenn auch mit erheblichen Verletzungen und
sogar Bewusstlosigkeit gerechnet werden muss.Trifft der Wagen nicht auf eine Mauer, sondern ein identsches und mit gleicher Geschwindigkeit entgegenkommendes Fahrzeug, so tritt die gleiche Beschleunigung auf. Beide Fahrzeuge kommen genau in der Mitte zwischen beiden zum Stillstand und haben somit den gleichen Bremsweg, als würden sie gegen eine an dieser Stelle angebrachte Wand fahren. Sind die Fahrzeuge unterschiedlich schwer oder unterschiedlich schnell, so haben beide unterschiedliche Beschleunigungen, die mit Hilfe des Impulserhaltungssatzes berechnet werden können.
Erfolgt der Aufprall mit
![v_1 = \unitfrac[50]{km}{h} \approx
\unitfrac[13,9]{m}{s}](../../_images/math/724c146568025b93016b907b4887d3e0b4c23a0c.png) oder
oder ![v_2 = \unitfrac[100]{km}{h} \approx
\unitfrac[27,8]{m}{s}](../../_images/math/b69938b637b9f1ec3ddf04832a4dfdc97c69ac5c.png) , so ergeben sich folgende Beschleunigungen:
, so ergeben sich folgende Beschleunigungen:![| a_1 | = \frac{v_1^2}{2 \cdot s} =
\frac{\left(\unit[13,9]{\frac{m}{s}}\right)}{2 \cdot \unit[0,5]{m}}
\approx \unit[193]{\frac{m}{s^2}} \\[8pt]
| a_2 | = \frac{v_2^2}{2 \cdot s} =
\frac{\left(\unit[27,8]{\frac{m}{s}}\right)}{2 \cdot \unit[0,5]{m}}
\approx \unit[772]{\frac{m}{s^2}}](../../_images/math/ddd4fde3b96b98629da51289bc4875d0ee4161c7.png)
Diese Beschleunigungen entsprechen rund
![\unit[20]{g}](../../_images/math/783c09424e2a1ddd66d41840d3e09ec157b2c550.png) beziehungsweise
beziehungsweise
![\unit[79]{g}](../../_images/math/27902edd3c5332122e7a33a4438326b2ab566a1f.png) und sind somit lebensgefährlich bzw. tödlich.
und sind somit lebensgefährlich bzw. tödlich.
Kreisförmige Bewegungen¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Kreisförmige Bewegungen.
Wenn die Schnur reißt, fliegt der Stein geradlinig in Richtung seiner Momentangeschwindigkeit
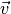 weiter, also senkrecht zu der
Richtung, welche die Schnur zum Zeitpunkt des Reißens hatte.
weiter, also senkrecht zu der
Richtung, welche die Schnur zum Zeitpunkt des Reißens hatte.Bei der kreisförmigen Bewegung handelt es sich somit um eine beschleunigte Bewegung: Auch wenn sich der Wert seiner Geschwindigkeit nicht ändert, so ändert sich auf einer Kreisbahn doch kontinuierlich die Richtung. Die dazu nötige (Radial-)Kraft wird mittels der Schnur auf den Stein übertragen.
Die Umlaufzeit des Kieselsteins kann anhand seiner Kreisfrequenz
![f =
\unit[1,8]{s}](../../_images/math/2ca3061b4ce1efc1e5a5de6dfef85c74f202b80c.png) berechnet werden:
berechnet werden:
![T = \frac{1}{f} = \unit[1]{\unit[1,8]{\frac{1}{s}} } \approx \unit[0,56]{s}](../../_images/math/7a0dd1c57dc7466bb9b2bd4c6feb7cbb5089e638.png)
Für die Winkelgeschwindigkeit
 des Kieselsteins gilt:
des Kieselsteins gilt:![\omega = \frac{2 \cdot \pi }{T} = 2 \cdot \pi \cdot f = 2 \cdot \pi
\cdot \unit[1,8]{\frac{1}{s} } \approx 11,3 \frac{1}{s}](../../_images/math/e5b8cf32453b54a4db5520a9969ee6f7d2792a50.png)
Für die Bahngeschwindigkeit
 des Kieselsteins auf seiner Kreisbahn
des Kieselsteins auf seiner Kreisbahn
![(r = \frac{d}{2} = \unit[36]{cm} = \unit[0,36]{m})](../../_images/math/915e57b01be2654a2a4ac23d47980f51b6880bc6.png) gilt:
gilt:![v = \omega \cdot r = \unit[11,3]{\frac{1}{s} } \cdot \unit[0,36]{m} =
\unit[4,07]{\frac{m}{s}}](../../_images/math/d7c7d0057ba3618a7fe7f645656b48cfd89d34c4.png)
Der Kieselstein hat somit eine Bahngeschwindigkeit von etwa
![\unitfrac[4,1]{m}{s} \approx \unitfrac[15]{km}{h}](../../_images/math/d8eb32c99c070a082059460186ad1e4c405ca656.png) .
.
Der PKW bewegt sich mit einer Geschwindigkeit von
![v =
\unitfrac[90]{km}{h} = \unitfrac[25]{m}{s}](../../_images/math/e9c9ee772fbdb3e51e88e0d1befbcdffdf45ae1a.png) ; mit dem Radius
; mit dem Radius ![r =
\frac{d}{2} = \unit[22,5]{cm} = \unit[0,225]{m}](../../_images/math/fef8b99dff37e01fb4fd07bda505ffdfd07eb5d1.png) folgt für die
Winkelgeschwindigkeit
folgt für die
Winkelgeschwindigkeit  der Räder:
der Räder:![\omega = \frac{v}{r} = \frac{\unit[25]{\frac{m}{s}}}{\unit[0,225]{m}}
\approx \unit[111,1]{\frac{1}{s}}](../../_images/math/31d3b96b774be64009a3abad322a62d07db39ccc.png)
Die Winkelgeschwindigkeit beträgt somit rund
![\unitfrac[111,1]{rad}{s}](../../_images/math/2f9141dee36e435b47629993dad80c813eadd27f.png) .
Da eine voll Umdrehung einem Drehwinkel von
.
Da eine voll Umdrehung einem Drehwinkel von 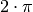 entspricht,
folgt für die Drehzahl
entspricht,
folgt für die Drehzahl 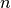 :
:![n = \frac{\omega}{2 \cdot \pi} = \frac{\unit[111,1]{\frac{1}{s}}}{2 \cdot
\pi} \approx \unit[17,7]{\frac{U}{s}}](../../_images/math/ac177866cc7b4fb51fad2df24e73f7295b2a10ab.png)
Das Rad führt in je Sekunde somit rund
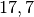 Umdrehungen aus.
Umdrehungen aus.
Die Bahngeschwindigkeit
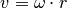 der Zentrifuge lässt sich
mit
der Zentrifuge lässt sich
mit ![n = \unitfrac[3000]{U}{min}](../../_images/math/9af7f26a681d859aef3cc308a9ef06371221a2b3.png) und
und ![r = \unit[0,0100]{m}](../../_images/math/74bd718fb5295e1072fed3edaeb55fe659af6911.png) folgendermaßen berechnen:
folgendermaßen berechnen:![v = \omega \cdot r = (n \cdot 2 \cdot \pi) \cdot r = \frac{3000 \cdot 2
\cdot \pi \cdot \unit[0,0100]{m}}{\unit[60]{s}} \approx
\unit[3,14]{\frac{m}{s}}](../../_images/math/998fb1f6735092777a648a26edb1da07c13920d6.png)
Damit folgt für die Radialbeschleunigung
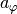 :
:![a_{\mathrm{\varphi}} = \frac{v^2}{r} =
\frac{\left(\unit[3,14]{\frac{m}{s}}\right)^2}{\unit[0,01]{m}} \approx
\unit[986]{\frac{m}{s^2}}](../../_images/math/60bd2823868f4aaf255444cc021fc484de91e205.png)
Die Radialbeschleunigung in der Zentrifuge beträgt bei der angegebenen Drehzahl rund
![\unitfrac[986]{m}{s^2}](../../_images/math/46a4c023ddce60234dca4067c005c5265554afb1.png) ; dies entspricht etwa dem
; dies entspricht etwa dem
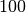 -fachen der Erdbeschleungigung
-fachen der Erdbeschleungigung 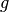 .
.
Um die Radialbeschleunigung zu bestimmen, welche die Erde auf einen Körper am Äquator ausübt, sollte zunächst die Bahngeschwindigkeit
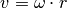 eines auf der Erdoberfläche mitrotierenden Körpers berechnet werden.
Auf Höhe des Äquators gilt mit
eines auf der Erdoberfläche mitrotierenden Körpers berechnet werden.
Auf Höhe des Äquators gilt mit ![r_{\mathrm{E}} = \unit[6370]{km}](../../_images/math/beb165c9a93c35c13f0fccb1d45b51aade414611.png) :
:![v = \omega \cdot r = \frac{2 \cdot \pi \cdot r}{T} = \frac{2 \cdot \pi
\cdot \unit[6370]{km}}{\unit[1]{d}} = \frac{2 \cdot \pi \cdot
\unit[6370 \cdot 10^3]{m}}{\unit[24 \cdot 60 \cdot 60]{s}} \approx
\unit[463]{\frac{m}{s}}](../../_images/math/40d2c1e8eb0d6bd675cf27dbbcf7421a24978fe5.png)
Damit gilt für die Radialkraftbeschleunigung
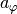 :
:![a_{\mathrm{\varphi}} = \frac{v^2}{r} =
\frac{\left(\unit[463]{\frac{m}{s}}\right)^2}{\unit[6370 \cdot 10^3]{m}}
\approx \unit[0,033]{\frac{m}{s^2}}](../../_images/math/174dddb94ef36fdaf3a8430eb0211ea404200f55.png)
Die Radialbeschleunigung beträgt am Äquator somit rund
![\unitfrac[0,033]{m}{s^2}](../../_images/math/759c7cf7ca4c26e79f6a5a125e06ba2a5e4c8a62.png) .
.Auf einem nördlich bzw. südlich vom Äquator gelegenen Punkt auf der Erde bewegt sich ein mit der Erde mitrotierender Körper auf einer Kreisbahn mit einem Radius
 , der kleiner als der Erdradius
, der kleiner als der Erdradius 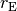 ist. Für
ist. Für  gilt in Abhängigkeit vom Breitengrad
gilt in Abhängigkeit vom Breitengrad 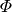 :
: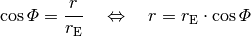
Für den 45. Breitengrad
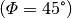 ergibt sich damit für
Rotationsradius
ergibt sich damit für
Rotationsradius  :
:![r = r_{\mathrm{E}} \cdot \cos{45\degree} \approx \unit[4\,505]{km}](../../_images/math/2ce5cb78881b557a3da880afb03ddecc42e6b7cf.png)
Für die Bahngeschwindigkeit
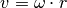 des rotierenden Körpers
und die Radialkraftbeschleunigung
des rotierenden Körpers
und die Radialkraftbeschleunigung 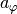 gilt somit:
gilt somit:![v = \omega \cdot r = \frac{2 \cdot \pi \cdot r}{T} = \frac{2 \cdot \pi
\cdot \unit[4505]{km}}{\unit[1]{d}} = \frac{2 \cdot \pi \cdot
\unit[4505 \cdot 10^3]{m}}{\unit[24 \cdot 60 \cdot 60]{s}} \approx
\unit[328]{\frac{m}{s}} \\](../../_images/math/779e0f8964faf44263dd16021db5dd5a51ff9e4f.png)
![a_{\mathrm{\varphi}} = \frac{v^2}{r} =
\frac{\left(\unit[328]{\frac{m}{s}}\right)^2}{\unit[4505 \cdot 10^3]{m}}
\approx \unit[0,024]{\frac{m}{s^2}}](../../_images/math/b8bbfbde96af20895095a449f6dced564e3b9ca2.png)
Die Radialbeschleunigung durch die Erdrotation beträgt am 45. Breitengrad somit rund nur noch
![\unitfrac[0,024]{m}{s^2}](../../_images/math/2d92a69b7fe4c61f3fd5cb6a1aa782b462a97b2e.png) . Am Nordpol
verschwindet sie völlig, da in diesem Fall
. Am Nordpol
verschwindet sie völlig, da in diesem Fall 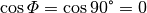 und somit
und somit 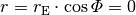 gilt.
gilt.Die Werte der Radialbeschleunigungen an den verschiedenen Stellen der Erde bewirken eine Verringerung der Erdbeschleunigung
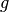 . An den Polen ist
daher
. An den Polen ist
daher ![g \approx \unitfrac[9,83]{m}{s^2}](../../_images/math/d322f746465ca3e285889dc4cc887ed29e5e08da.png) , in mittleren Breitengraden
ist
, in mittleren Breitengraden
ist ![g \approx \unitfrac[9,81]{m}{s^2}](../../_images/math/1a0dae3c9a4e2601a3e1305b55efe9f6fd06583e.png) , und am Äquator ist
, und am Äquator ist ![g
\approx \unitfrac[9,78]{m}{s^2}](../../_images/math/0ca182d8ba8ba9f37ad9bbeab4c6734d3aba1180.png) . Obwohl die Unterschiede nur gering sind, so
hatten sie doch im Laufe der Erdgeschichte eine leichte Abplattung der Erde zu
den Polen hin zur Folge: Am Äquator beträgt der Erdradius
. Obwohl die Unterschiede nur gering sind, so
hatten sie doch im Laufe der Erdgeschichte eine leichte Abplattung der Erde zu
den Polen hin zur Folge: Am Äquator beträgt der Erdradius
![r_{\mathrm{E}} \approx \unit[6378]{km}](../../_images/math/092fc510088b4a0da4fddc404eacd18348502e1a.png) , am Nord- bzw. Südpol hingegen
„nur“
, am Nord- bzw. Südpol hingegen
„nur“ ![\unit[6370]{km}](../../_images/math/47abcc3e9499cd364bd5b81f724598a843e83786.png) .
.
